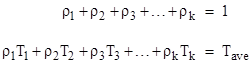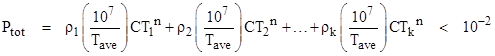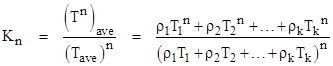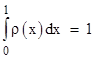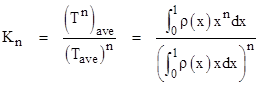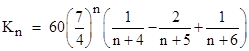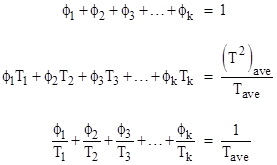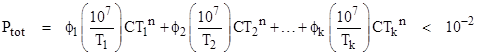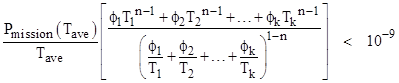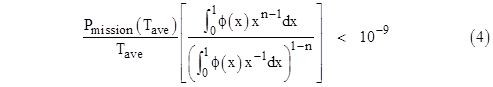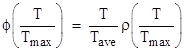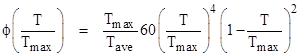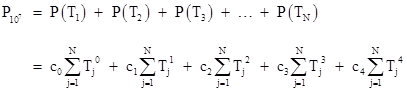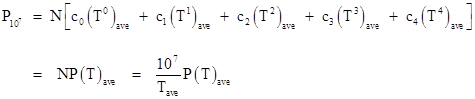Regulating Risk

Suppose the probability of a complete system failure in 10 million operational hours is required to be less than 1/100, and the system performs a series of missions of various durations.  If the average mission length is T_ave, then the number of missions in 10 million hours is 10⁷/T_ave, and if the probability P_mission of complete failure for any individual mission was independent of mission length, then the probability of a complete failure in 10 million hours is (10⁷/T_ave)P_mission. (Since the probabilities are small compared with 1, we make use of the approximation 1 – e^−λt = λt, and we approximate the probability of the union of two independent events as the sum of their probabilities.) Therefore, the requirement for the probability of complete failure in 10⁷ hours of operation be less than 10⁻² implies that

However, if the probability of failure during a given mission depends on the duration of the mission, the situation is more complicated. In general, if a system contains redundancy such that n independent failures (with constant rates) must occur jointly on a single mission to result in complete system failure, then the probability P_mission(T) of complete failure for a given mission of duration T is typically proportional to the nth power of T. In other words, we have

for some constant C. The case n = 0 corresponds to risks that have the same probability per mission, regardless of mission duration, which is the case we considered originally, leading to the requirement P_mission/T_ave < 10⁻⁹. If n is greater than 0, we need to consider the effect of varying mission lengths to determine the corresponding requirement.

We begin by considering a discrete distribution of mission lengths, and then generalize to continuous distributions. Let ρ_j denote the fraction of missions that have duration T_j (arranged in ascending order), for j = 1 to k. Thus we have

As before, the total number of missions in 10⁷ hours of operation is 10⁷/T_ave, so the basic requirement can be expressed by summing the probabilities of the individual missions as follows:

Thus we have the required condition

The quantity in parentheses is simply (Tⁿ)_ave. Making use of equation (2), we have C = P_mission(T_ave)/T_aveⁿ, so we can make this substitution to give

where

Equation (3) differs from equation (1) only by the factor K_n, but we see that this factor is identically equal to 1 if n = 0 or if n = 1. However, for values of n greater than 1, the factor differs from 1. Thus, for dual redundant (or triple-redundant, etc.) systems, we must account for this extra factor to give the strictly correct requirement. The denominator of K_n depends only on the arithmetic average (weighted by number of missions) of the mission lengths, but the numerator is the arithmetic average of the nth powers of the mission lengths, so to evaluate the numerator we need to know the distribution of mission lengths.

It’s easy to extend this to a continuous distribution. Let ρ(x) denote a continuous density distribution as x ranges from 0 to 1. Thus we have

Letting T_max denote the maximum possible mission length corresponding to x = 1, we can put T = xT_max, and we arrive again at equation (3), except that now the factor Kn is given in terms of the corresponding integrals as

As in the discrete case, K_n is identically equal to 1 if n = 0 or 1, and for larger values of n the value of K_n depends on the distribution of mission lengths. To illustrate, suppose the mission lengths are distributed according to a beta distribution

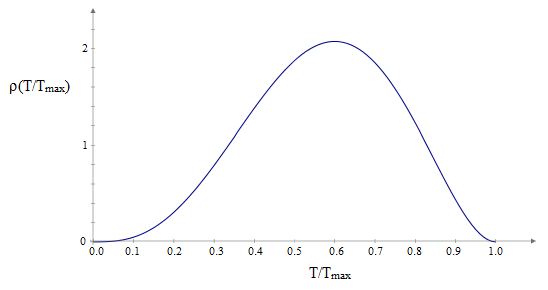
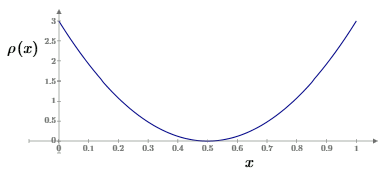
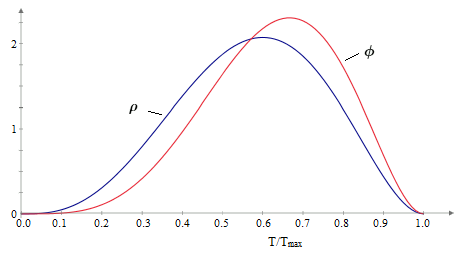
Choosing a = 3 and b = 2, this gives the distribution function ρ(x) = 60x³(1−x)², which is plotted below.

With this distribution of mission lengths, we have T_ave/T_max = 4/7, and the factor K_n is

Of course, by construction, we have K₀ = K₁ = 1. For n = 2, 3, and 4 we have K_n = 1.09, 1.27, and 1.56 respectively. (To be precise, the exact values are 35/32, 245/192, and 2401/1536.) This shows that, even for highly redundant systems, the extra factor is not extremely significant for establishing the probability of a complete failure in 10 million operational hours, so the neglect of this factor in common practice is justified. However, it should be noted that although the average probability is not significantly affected, the variability of P_mission is obviously significant for n > 0. For example, with n = 0 the probability of failure for a mission with T/T_max = 0.2 is exactly the same as for a mission with T/T_max = 0.8, and yet with n = 2 the longer mission is 16 times more likely to fail than the shorter mission, and with n = 3 it is 64 times more likely to fail than the shorter mission. So, concerns about variations in “specific risk” of individual missions due to variations in mission duration should focus on systems with large values of n.

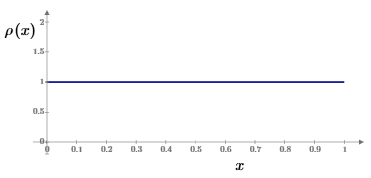
The beta distribution discussed above is fairly realistic for many applications, but we can also consider other distributions. One particularly simple distribution is ρ(x) = 1, which signifies that the mission times are uniformly distributed between 0 and T_max, as shown below.

For this distribution we have T_ave = T_max/2, and the required condition on probabilities can be written in the form of equation (3) with

On the other hand, if we want to consider the possibility that the mission lengths are split into some very short missions and some very long missions, we could posit a parabolic distribution such as ρ(x) = 12(x – 1/2)², as shown in the figure below.

For this distribution we again have T_ave = T_max/2, but the value of K_n is

As always, the coefficient is unity for n = 0 or 1. To compare these distributions, we note that with n = 4 the beta distribution gives K_n = 1.56, the uniform distribution gives K_n = 3.20, and the parabolic distribution gives K_n = 5.02. This suggests that for the beta distribution we might be justified in neglecting this factor, but if the mission durations are distributed uniformly or concentrated at the extreme high and low durations, the factor should be taken into account.

Incidentally, it’s possible to characterize the distribution of mission lengths on a different basis, due to the ambiguity inherent in the decision of whether to allocate risk per mission or per operational hour. In the preceding discussion we weighted the durations by the number of missions. For example, suppose we have 1000 missions, half with T₁ = 1 hour and half with T₂ = 9 hours. Accordingly our discrete density factors would be ρ₁ = 0.5 and ρ₂ = 0.5, and the average duration would be (0.5)1 + (0.5)9 = 5 hours. However, one might question whether this is the most appropriate weighting of the mission lengths. Notice that the system spends 9 times as much time operating on mission of 9 hours as it spends operating on mission of 1 hour. Thus if we sample the system at random times, we are 9 times more likely to find it on a 9-hour mission as on a 1-hour mission. This might lead someone to weight the mission durations by the fraction of the total 10⁷ operational hours spent in missions of each duration, rather than by the fraction of the total number of missions. They might even argue that the appropriate “mean” mission duration is (0.1)1 + (0.9)9 = 8.2 hours.

To consider this in more detail, let ϕ_j denote the fraction of operational time spent on missions of duration T_j (arranged in ascending order), for j = 1 to k. Thus we have

where T_ave is the arithmetic mean. The total number of missions of duration T_j in 10⁷ hours of operation is ϕ_j10⁷/T_j, so the basic requirement can be expressed as

Thus we have the required condition

Again making use of equation (2), we have C = P_mission(T_ave)/T_aveⁿ, so we can make this substitution to give

We also note that the denominator of that factor is simply T_aveⁿ⁻¹. Taking this to the limit for a continuous distribution f(x) gives

Again we see that the factor in square brackets is unity for n = 0 or 1, and differs from unity for larger values of n. To determine the values of this factor, and compare them with the values we found using the mission-based distribution, we cannot simply use the same distribution function directly, because that represented the distribution of mission times weighted by the number of missions, whereas here we need the distribution of mission times weighted by the number of operational hours. In general the ϕ distribution that corresponds to any given ρ distribution is

For the particular distribution plotted previously, this gives

Since T_max/T_ave = 7/4, we get the time-weighted density distribution ϕ(x) = 105x⁴(1−x)² where x = T/T_max. This is more heavily weighted toward the longer mission lengths, as shown in the plot below.

As expected, using this distribution for ϕ(x), we find that the quantity in square brackets in equation (4) has the values 1.09, 1.27, and 1.56 corresponding to n = 2, 3, and 4 respectively, identical to the values found using the corresponding mission-weighted distribution.

In the preceding discussion we focused on failures for which the probability per mission is proportional to some specific power of the mission duration. More generally, the probability per mission of duration T could be a combination of such terms, i.e.,

(It would be extremely unusual for the probability per mission to contain a term proportional to the fifth or higher power of the mission duration, since this would correspond to a cutset with five or more elements, each with a full mission exposure time.) The benchmark fleet life of 10⁷ hours is composed of N missions of duration T₁, T₂, …, T_N, and we have the relations

Assuming the probabilities are small enough so that the probability of the union of events is simply the sum of the individual event probabilities, and noting that the total probability of one catastrophic failure in 10⁷ hours is less than 1/100, so the probability of two or more such failures is a negligible contributor to the probability of one or more, it follows that the probability of a catastrophic failure in 10⁷ hours is

where the unsubscripted P signifies the mission probability. Each of the summations can be written as N times the average of the respective power of T, so we have

This probability must be less than (or “on the order of”) 1/100, so we have the requirement

This differs from the usual regulatory requirement, which is expressed as P(T_ave)/T_ave < 10^–9/hr. As explained above, the value of P(T)_ave is not the same as P(T_ave). In other words, the average probability per mission for a given distribution of mission lengths is not (in general) the same as the probability of a mission of average duration. The factor relating these two values was described above for the case when the probability is proportional to one specific power of the mission length. For the more general case, where the probability is a polynomial function of the mission time, the applicable factor is a weighted average of the factors for the individual powers. Therefore, it would be acceptable to use the factor for the highest relevant power.

Return to MathPages Main Menu