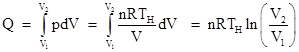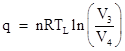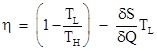Reasoning With Reversibility

The second law of thermodynamics was originally expressed by Rudolph Clausius (1822-1888) as the assertion that heat always from higher to lower temperature, never from lower to higher (all else being unchanged). This is equivalent to the statement that it’s impossible to convert a given amount of heat entirely into mechanical work (again, leaving all else unchanged). The equivalence of these two statements is not immediately self-evident, but it follows from some simple reasoning about reversible processes, combined with some facts about the behavior of an ideal gas.

Before describing this reasoning in detail, it’s worthwhile to ask why we should care about these two statements. In particular, why do we care about processes that turn heat into mechanical work? A device that performs such a process is called a heat engine. According to the first law of thermodynamics, energy is always conserved, so we obviously cannot “produce” energy with a heat engine. We put energy into the process in the form of heat, and extract a (generally lesser) amount of energy from the process in the form of mechanical work. The reason for doing this is that energy in the form of mechanical work is often more useful than the same amount of energy in the form of heat. In a sense, mechanical work is coherent energy, whereas heat energy is incoherent. On the microscopic scale the individual molecules of a heated gas within a rigid container do work when they collide with the walls, exciting the molecules of the walls, elevating the temperature of the container. But on a macroscopic scale this process appears as just a flow of heat from the gas to the container walls, because it represents the transference of incoherent energy from one place to another. In both the gas and the walls, the energy is in the form of randomly moving molecules. On the other hand, if we allow one wall of the container to be displaced outward by the physical pressure of the gas, there is a coherent movement of all the molecules in that wall. This forced coherent movement represents mechanical work. Just as in the case of heat flow, the transference of energy is due to collisions between the molecules of gas and the wall, but in one case the macroscopic wall is held stationary and it absorbs the energy as heat, whereas in the other case the macroscopic wall is allowed to move (macroscopically), and it thereby has mechanical work done on it.

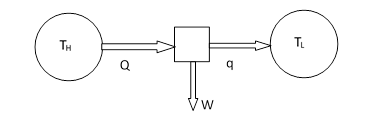
A conceptual schematic of a heat engine is shown below. Two channels of heat transfer, with thermal reservoirs of two different temperatures T_H and T_L, are shown, along with one channel of work transfer.

The thermal reservoirs are assumed to be large enough that their temperatures don’t change as heat flows in or out of them. The arrows indicate the direction of energy transfer (heat flow or work) in the forward time direction. According to the first law of thermodynamics we have Q = W + q. The efficiency η of this engine is defined as the ratio of work energy output to the heat energy input, so we have η = W/Q = 1 – q/Q.

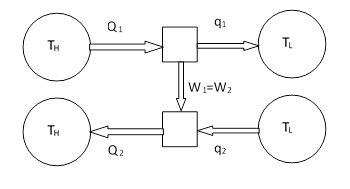
If all the energy transfer processes in a given heat engine are reversible, we can just as well reverse all the arrows, and run the heat engine “backwards in time”. (A kitchen refrigerator is a common example of a heat engine running in reverse.) Suppose we have two different reversible heat engines, and we run one of them in the forward direction and one in the reverse direction. We can scale the machine so the rates of work are equal, and link them together as shown below.

Since these are two different engines, possibly operating by means of very different physical processes, we have not assumed that their efficiencies or heat flows are the same for a given rate of work. The only assumption is that both engines are reversible, i.e., can be run in either the forward or reverse direction. The first law of thermodynamics tells us that Q₁ = W₁ + q₁ and Q₂ = W₂ + q₂, and since the work rates are equal, we have the relation Q₁ – q₁ = Q₂ – q₂. Taking the two processes together, the net flow of heat from the reservoir at T_H to the reservoir at T_L is Q₁ – Q₂, which of course equals q₁ – q₂. This implies that if Q₂ is greater than Q₁, there is a net flow of heat from the low temperature reservoir to the high-temperature reservoir, in contradiction to Clausius’ statement of the second law of thermodynamics. Hence we conclude that Q₂ cannot be greater than Q₁. Furthermore, by running the combined processes in reverse, the very same reasoning shows that Q₁ cannot be greater than Q₂. Thus we have Q₁ = Q₂ and q₁ = q₂, from which it follows that 1 – q₁/Q₁ = 1 − q₂/Q₂. Therefore, based solely on the first and second laws of thermodynamics, we find that every reversible process operating between two given temperatures has the same efficiency. Of course, this analysis also shows that no heat engine can be more efficient than a reversible one, because the heat flowing from the high-temperature reservoir into such a putative super-engine would be less than the heat flowing back into that reservoir from a reversed engine with matched work, and hence there would be a next flow of heat from the low to the high temperature reservoir, in violation of the second law.

These are very significant results, and they greatly simplify the task of determining the highest possible efficiency of any conceivable heat engine, because we need only determine the efficiency of a reversible engine – any reversible engine – and we are guaranteed that the efficiency of every other heat engine, regardless of its construction method of operation, must have exactly the same efficiency, and this is the maximum possible efficiency for any heat engine (consistent with the first and second laws of thermodynamics).

We defined a reversible process as one which can equally well proceed in the forward or reverse time direction. A sufficient condition for this to be true is if the process proceeds quasi-statically, which is to say, at each instant during the process the system is essentially in static equilibrium. (In general this is not a necessary condition, as shown by the reversibility of macro-dynamic processes such as planetary orbits, but it is necessary for thermodynamic processes.) For example, by slowing modulating the volume and the flow of heat into and out of a quantity of ideal gas, we can carry out a completely reversible cycle, i.e., one which could be carried out in either temporal direction. If we represent the state of the gas by a point on a plot of pressure versus volume, we can imagine a process that follows any arbitrary closed loop, such as the one illustrated in the figure below.

This will be reversible provided we arrange for heat to flow into or out of the gas at each point on the path such that the temperature is always in equilibrium (or nearly so) with the pressure and volume according to the ideal gas law pV = nRT. Thus for each point on the path the temperature must equal to pV/nR. (The reason for going slowly is to allow the heat to flow in and out of the gas with minimal thermal gradients, because such gradients are departures from equilibrium.) The shaded area inside the loop represents the net work performed by the boundary of the gas during the cycle.

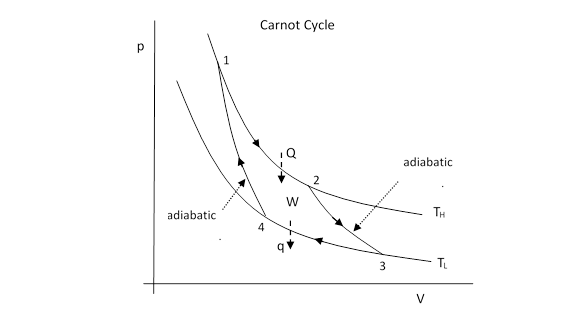
In 1824 the French scientist Sadi Carnot (son of Lazarre Carnot, organizer of victory in the French Revolution) described a particularly simple reversible cycle, which is now known as the Carnot cycle. It consists of four steps. First is a period of expansion during which heat is added to maintain constant temperature. Next, the expansion is allowed to continue but without any transfer of heat, so the pressure and temperature drop as the volume increases. (This is called adiabatic expansion, signifying that the only energy transfer during the process is work.) For the third step, the gas is compressed and heat is extracted so as to maintain constant temperature. During the fourth step, to complete the cycle, the gas is compressed still further, but is isolated from any heat flow, so temperature and pressure both rise as the volume is reduced. (This is called adiabatic compression.) These four steps are carried out in such a way that the final state is identical to the initial state, as shown in the figure below.

During the isothermal expansion the pressure if related to the volume by p = nRT_H/V, and the heat Q added to the gas must equal the work done by the boundary during this phase (because at constant temperature the internal energy of the gas remains constant). Thus we have

By the same reasoning the heat rejected during the isothermal compression phase is

so the ratio of the rejected heat to the applied heat is

We now make use of the facts (for an ideal gas) that during an isothermal process the quantity pV is constant, and during an adiabatic process the quantity pV^γ is constant, where γ is the ratio of specific heats for the gas. Thus we have

Equating the product of the left sides with the product of the right sides and canceling the pressures, we get (V₂/V₁)^γ−1 = (V₃/V₄)^γ−1 and therefore V₂/V₁ = V₃/V₄. Substituting into the previous expression for q/Q we arrive at the result q/Q = T_L/T_H, so the efficiency of a reversible heat engine operating between the temperatures T_L and T_H is simply

Another approach to determining the efficiency of a reversible cycle (operating between two fixed temperatures T_H and T_L) is based on general considerations of the entropy δS = δQ/T. If a heat engine is cyclic, it returns to the same thermodynamic state periodically, so there is no net change in its entropy over a complete cycle. On the other hand, there is a change in entropy of −δQ/T_H for the high-temperature reservoir, and a change of δq/T_L for the low-temperature reservoir, where δQ and δq are the amounts of heat flow for a single cycle. We also know that δq = δQ + δW, so the overall change in entropy δS over a cycle can be written as

Dividing through by δW and solving for the efficiency η = δW/δQ, we get the result

This shows that a cyclic heat engine is reversible if and only if the change dS in entropy is zero, and it also establishes the link between Clausius’ statement of the second law and the statement that entropy never decreases.

The preceding “derivation” of reversible efficiency in terms of the temperature ratio essentially amounts to a definition of thermodynamic temperature. Since the efficiency of a reversible heat engine depends on nothing other than the two temperatures between which it operates, we can arbitrarily assign a value, say, 273.16 deg K, to a standard physical reference state (the triple point of water), and then the temperature of every other state is defined based on the ratio of heat flows for a reversible engine operating between that temperature and the reference temperature. In this way we arrive at the absolute thermodynamic temperature scale. This scale has the added benefit of being consistent with the definition of temperature given by the ideal gas relations.

Return to MathPages Main Menu