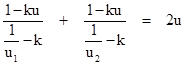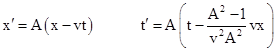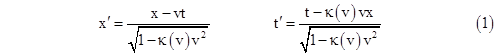Conditions for Relativity

An inertial coordinate system is a system of space and time coordinates with respect to which the descriptions of the motions of material bodies are particularly simple and symmetrical. More precisely, an inertial coordinate system is defined as a system of space and time coordinates with respect to which

(i) any material particle that is not subjected to external influences moves at constant speed in a straight line, and

(ii) if two identical particles, initially at rest, act to repel each other, they will acquire equal speeds in opposite directions.

We sometimes refer to propositions (i) and (ii) as "laws of motion", but of course they are true only when motion is described in terms of inertial coordinates, which are defined as coordinates in terms of which (i) and (ii) are true. Hence these "laws of motion" are actually tautological, i.e., true by definition. On the other hand, we have no a priori reason to believe that the definition of inertial coordinate systems has any applicability. Nothing guarantees us the existence of such coordinate systems, which is to say, nothing guarantees us that the motions of material bodies satisfy propositions (i) and (ii) with respect to any single system of coordinates. Our belief that such coordinate systems do exist (at least approximately) is inferred from experience. In fact, our experience has led us to infer not only the existence of one inertial coordinate system, but the existence of infinitely many, such that

(iii) for any material body in any state of motion there exists an inertial coordinate system with respect to which that body is instantaneously at rest.

Setting aside the historical fact that proposition (iii) - which is usually called the principle of relativity - was inferred from experience, it's interesting to consider under what conditions this principle actually follows immediately from the existence of a single inertial coordinate system. Given one inertial coordinate system, we can certainly construct another coordinate system in terms of which any given object is momentarily at rest, and by making the transformation from the original inertial coordinate system to this new coordinate system linear, we can ensure that proposition (i) applies to the new coordinate system. In other words, if an object moves at constant speed in a straight line with respect to the original inertial coordinate system, it will also do so with respect to this new coordinate system. In addition, we are free to choose a time axis tangent to the worldline of any material object in any state of motion, so that this object is momentarily at rest with respect to this system. It remains to determine whether we can always define this new coordinate system so that proposition (ii) also applies. If so, then the "principle of relativity" (iii) follows.

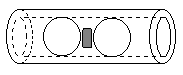
So far no restriction has been placed on the tangent direction of the space axes, nor on the scale factors of the axes. By selecting suitable directions and scale factors, can we necessarily ensure that proposition (ii) is true? In other words, can we choose the space axes and scale factors in such a way that any two mutually repelling objects initially at rest acquire equal speeds in opposite directions? (This symmetry is referred to as inertial isotropy, because it corresponds to the equality of the effects of inertia in all spatial directions.) We can certainly ensure inertial isotropy for one particular pair of objects repelling each other with some specified impulse, but it does not follow that there exists a single system of coordinates with respect to which all pairs of identical resting objects would exhibit inertial isotropy. To explore the possibilities, we could use a device such as the one shown below, consisting of two identical pellets in a cylinder with a small explosive charge between them.

When this apparatus is at rest (aligned with the x axis) with respect to our posited inertial coordinate system and the charge is detonated, the pellets are ejected with equal speeds in opposite directions, in accord with the definition of an inertial coordinate system. This is true regardless of the strength of the explosive charge, or the masses of the pellets. Now if we place the same apparatus in motion (along the x axis) with a speed u and detonate the charge, we can evaluate the speeds of the two pellets with respect to the original inertial coordinate system. If we invariably find that the pellets have speeds u+v and u–v we can easily define another inertial coordinate system. However, we are not entitled to assume, a priori, that material objects behave this way.

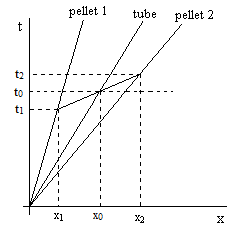
In order to achieve relativity, the tube must have a speed of 0 and the pellets must have equal and opposite speeds of +v and –v with respect to our new coordinate system, but the composition of these speeds with the speed u defined with respect to the original system can only be determined empirically. In general, let f(u,v) denote the speed of an object with respect to the original coordinate system if the object has the speed v with respect to our new coordinate system whose spatial origin has the speed u with respect to the original system. Thus after the charge has been detonated in a tube moving with speed u, we find that the pellets are moving with speeds u₁ = f(u,–v) and u₂ = f(u,+v) with respect to the original coordinate system. (The value of v is arbitrary, depending on the strength of the explosive charge and the (rest) masses of the pellets.) The result is as shown below.

The worldlines of the two pellets and the tube are

and the space axis of our new coordinate system for the frame in which the tube is at rest must be parallel to the line

where the slope k is a function of u. Substituting from the pellet worldlines and solving for x₁ and x₂, we have

Now, inertia is isotropic with respect to our new coordinate system if and only if x₂ - x₀ equals x₀ - x₁, which is equivalent to x₁/t₀ + x₂/t₀ = 2u. Thus we must have

Clearing the fractions and simplifying, this leads to the condition

Solving this for k, we have

If we take k = 0 this condition reduces to

which of course is satisfied by the composition function f(u,v) = u + v. However, if we define h = k/u the condition becomes

which is satisfied by the composition function f(u,v) = (u+v)/(1+huv). Note that, since u, v, and f(u,v) are the pairwise speeds between three systems of inertial coordinates, the expression for any one of them in terms of the other two must be of the same form and single-valued, so this must be a linear fractional transformation with constant coefficients. Now, since f(u,0) = u, any linear fractional transformation for the speed composition function is of the form f(u,v) = (u+gv)/(1+huv) where h and g are constants, and we can substitute into the expression for k to give k = (h/g)u. It is also common to impose the requirement of reciprocity, which means that

(iv) if the new coordinate system is moving with speed u relative to the original system, and an object is moving with speed v = –u with respect to this new system, then it is at rest with respect to the original system.

In other words, we require f(u,–u) = 0, which implies g = 1 and hence k = hu as before. This leaves us with the speed composition formula

where h is a constant with units of an inverse squared speed. The very fact that energy has inertia implies that h is not zero. More precisely, it can be shown that if an object with total energy E has inertial mass E/c², then h = 1/c².

The final requirement for complete relativity is that, in terms of our tube apparatus

(v) the numerical speeds of the ejected projectiles with respect to the rest frame of the tube depend only on the rest masses of the projectiles and the energy of the explosive charge, independent of the velocity of the tube relative to the original inertial coordinates.

This is a somewhat complicated proposition, because it requires us to compare the energy contents of two explosive charges at rest with respect to two different coordinate systems. In proposition (ii) we referred to two identical pellets, but these were side-by-side at rest with respect to each other, and could simply be interchanged, whereas proposition (v) involves the notion that we could produce two identical explosive charges, then accelerate one of them into a different state of motion, and then assert that the two charges have equal energies relative to their respective rest frames. From another point of view, it could be argued that we simply define this to be true, or perhaps it is more accurate to say we adopt it as an organizing principle, similar to conservation of energy. The variety of ways in which energy can be stored makes it difficult to analyze this proposition on a more fundamental basis. In any case, it certainly imposes a restriction on the scale factors, and we have no a priori reason to expect that any system of coordinates will satisfy this requirement for all possible energies and masses. Again, the existence of such coordinates can only be established empirically.

With these stipulations, we've exhausted all the continuous degrees of freedom for defining the new coordinate system, and we've indicated the main empirical conditions that must obtain in order to ensure that this new system of coordinates can be defined in such a way as to yield relativity, as summarized by propositions (i) through (v). However, we have not (so far) uniquely identified the transformation that relates two different systems of inertial coordinates. We have simply described (roughly) a procedure that is guaranteed to determine an inertial coordinate system with respect to which any given material body is momentarily at rest, and that will be relativistic assuming relativity is possible. This procedure involves actual observations of the motions of material bodies, and it is those motions that determine not only whether relativity is possible, but also (if it is) the relationship between two different systems of inertial coordinates. The only explicit prior constraint we have so far placed on the transformation between two inertial coordinate systems is that it be linear, so if x,t is one inertial coordinate system and x′,t′ is another, with a fixed mutual velocity of v along the x axis, then there are constants A, B, C, D such that x′ = Ax + Bt and t′ = Cx + Dt. However, we also have some implicit information about the transformation. For example, we know the velocity of the spatial origin of the x′,t′ coordinates has a velocity v = dx/dt with respect to the x,t coordinates. Thus the first transformation equation gives dx′ = Adx + Bdt = 0 and so B = –vA. We also have the inverse transformation x = (Dx′ - Bt′)/M, t = (–Cx′ + At′)/M where M = AD-BC, so by reciprocity we know that B = –vD and therefore A = D. Lastly, we can choose the scale factors so that the determinant M of the transformation is equal to 1. Combining all these conditions, we know the transformation is of the form

where A is some function of v. The important point to recognize is that the function A(v) is fully determined by the motions of material bodies. For any given v there is only one value of A that will yield coordinates x′,t′ with all the properties of an inertial coordinate system. Letting κ(v) denote the coefficient of vx in the above expression for t′, the transformation can be written in the form

Everyday observations tell us that the value of κ must be extremely small, if not actually zero, because in many cases (when v is not too large) the relationship between two systems of inertial coordinates is given very accurately by x′ = x-vt, t′ = t. Indeed this is the relationship that Galileo and Newton assumed to be exact. However, more precise observations involving larger relative velocities have shown that the value of κ is not precisely zero. Dimensionally it can be seen that κ has units of a squared inverse speed, and empirically it has been found to be constant with a value of κ = 1/c² where c is the speed of light in vacuum. To appreciate the smallness of this value, we can give it explicitly as

It's hardly surprising that such a small non-zero value was overlooked for so long, and even today it is often sufficiently accurate to simply take κ = 0. Only when dealing with very high relative velocities is it necessary to take account of the true value when dealing with the motions of material bodies.

Incidentally, the speed composition formula corresponding to transformation (1) is

so we see that κ(u) can be identified with the arbitrary function that we previously called h(u). It's interesting to consider how things would appear if this function was not constant. We could, for example, take κ(u) = sin(πu/2)/c², which would give the Galilean formula at u = 0 and the special relativistic formula at u = 1. However, if we extend the reciprocity condition to require the general symmetry f(u,v) = f(v,u), it follows that κ(u) must equal a constant.

Remarkably, it turns out that transformation (1) with κ = 1/c² is precisely the relationship between coordinate systems with respect to which Maxwell's equations of electro-magnetism are valid. Hence this transformation, called the Lorentz transformation, allows us to relativize not only the mechanics of material bodies, but the dynamics of electromagnetic fields as well. In fact, all known physical processes have been found to be locally "Lorentz invariant", and this has naturally led to the idea that the meaning of this transformation transcends its individual applications, and represents something fundamental about the nature of space and time. It's easy to show, based on this transformation, that if two events are separated in space and time by dx and dt with respect to one system of inertial coordinates, and by dx′ and dt′ with respect to any other, then (dt)² - (dx)² = (dt′)² - (dx′)². (Here we have chosen units of space and time so that c equals unity.) Since this quantity is invariant, it has come to be regarded as the absolute (squared) spacetime interval between two events. This is borne out by the fact that the phase of the quantum wave function of a system advances in proportion to this invariant interval as the system passes from one event to another. The quantum wave function is the most fundamental entity known to modern physics, and as far as we know there is no underlying structure ("hidden variables"). In fact there are severe restrictions, both theoretical and empirical, on even the possibility of any more fundamental structure underlying the quantum wave function. Consequently the Minkowski interval has come to be regarded as the actual fundamental metric of a unified spacetime manifold.

However, this view is sometimes challenged. For example, there is a school of thought that maintains that the only suitable framework within which to think about physics is Galilean space and time, and that it is useful to interpret all processes with respect to one particular "absolute rest frame" with a unique time coordinate. One of the obscure aspects of this approach is the nature of the "absolute rest frame". Some proponents of this "absolute" viewpoint imagine an "ether" with respect to which all motions are referred, but which is distinct from spacetime itself. They regard this ether as an entity in its own right, with its own state of motion, which they take to be the "absolute rest frame" simply because all motions are evaluated with respect to it. Hence (ironically) this viewpoint is actually highly relational, in the sense that it seeks to attribute all physical effects to the relations between entities. It just so happens that one of the entities in this relational world is the "ether". Whether this ether is or is not at absolute rest in space and time is a question that proponents of such theories seldom consider, which is perhaps understandable, because if all motion is to be defined only with respect to the ether, we can hardly define motion of the ether itself. This, in turn, leads to further difficulties for those etherists who wish to regard certain physical phenomena (e.g., light) as the result of "oscillations" or "undulations" of the ether. If these are to be understood as slight variations in the positions of different parts of the ether (as naive etherists often suggest), then clearly there must be some other reference (a meta-ether?) with respect to which these motions of the ether can be defined. Overall, it's a mistake to regard such ether theories as "absolutist" theories, because they are really the most relational of all theories of motion - notwithstanding the fact that proponents of such theories generally fail to notice this.

On the other hand, there are advocates of a genuinely absolutist approach, who, if they refer to "the ether" at all, regard it as simply the manifold of space itself. Obviously with this approach one cannot speak about oscillations or undulations of "the ether" unless one is willing to contemplate variations in the metric of space (and time?), which is typically anathema to the proponents of such theories. So, the ether is regarded as simply defining the absolute structure of space (in time), and this structure is typically taken to be Euclidean (and three-dimensional) with a single absolute "now" (or rather, a sequence of absolute "now"s.) In order to account for the apparent Minkowskian structure of spacetime, advocates of the absolutist approach usually avail themselves of the assumption that the structure of absolute space somehow imposes a fixed upper bound on the speed of propagation of all forms of matter and energy.

A fixed upper bound on speeds may simply be adopted as a bare assumption, but some absolutists suggest that it follows in a constructive way from a mechanistic or quasi-mechanistic model. For example, they may regard electromagnetic radiation as an unequivocally wave-like mechanistic phenomenon, from which (they say) we can deduce that it propagates in a mechanistic way at a characteristic speed with respect to the posited absolute frame. The difficulties with this approach are obvious, considering that the classical wave model of light leads to the "ultra-violet catastrophe" for black-body radiation, and is unable to account for the photo-electric effect, stimulated emission, the two-slit experiment, the Hanbury-Twiss effect, EPR experiments, and so on. Any claim to have deduced the logical necessity of a fixed upper bound on light propagation speed from the wave-like nature of light is undermined by the empirical fact that light does not propagate as a classical wave. Of course, this doesn't prevent us from guessing that, nevertheless, light has a fixed speed of propagation with respect to some system of reference, and we may even adopt this guess as a principle on which to base our theory, but we can't legitimately claim to have deduced this fact. This is essentially what Einstein did, when he inferred that the invariance of light speed was, in some sense, the manifestation of a fundamental principle, independent of the micro-structure of electro-magnetic radiation.

We should also point out that, unless the absolutist is prepared to embrace a substantial mechanistic ether, he cannot legitimately claim to possess a mechanistic justification for the fixed propagation speed of light, even with respect to just his posited absolute reference frame. If he regards the ether as simply the fixed framework of space itself, then any wave-like phenomena could only be of entities within (or secondary properties of) the different parts of this framework. But this, in turn, requires him to supply the mechanics of these entities or properties. At this stage he can avail himself of the classical field concept, but in so doing he abandons the mechanical paradigm.

Of course, even if there was a valid mechanistic model of light from which a fixed upper bound on the speed of light (with respect to the posited absolute system of reference) could be deduced, this does not imply that the same upper bound applies to all forms of energy. The notion of certain 19th century scientists that it might be possible to construct a theory in which all forms of matter and energy are essentially electromagnetic in nature has long since been abandoned as untenable, and in retrospect we can see it was doomed from the start, because classical electromagnetism is strictly linear (i.e., solutions are additive) so it cannot possibly yield stable bound configurations. (See Earnshaw’s Theorem.) Thus it has always been clear that there must exist important non-electro-magnetic effects, and therefore carrying over a conclusion about propagation speed from electromagnetic considerations to effects that are necessarily not electromagnetic can only be seen as a bold hypothesis, not a logical deduction, let alone a deduction based on mechanistic principles.

Furthermore, even if we stipulate a single finite upper bound for the propagation of all forms of energy, this still does not ensure the existence of inertial coordinate systems in relative states of motion. As explained previously, the motions of material bodies must satisfy several fairly restrictive conditions in order for it to be possible to define relatively moving inertial coordinate systems. A coherent spacetime representation of events is possible only because all the motions of inertial bodies conform to a single pattern with only a small number of degrees of freedom, so that they can be accommodated by our free choices in defining the axis directions and scale factors of our coordinate systems. This is typical of the kind of conditions that must be met in order for there to exist a viable geometrical interpretation. For example, given a set of n particles there are n(n-1)/2 pairs, and each pair could have a "separation", and there is no a priori reason to suppose that these separations must satisfy any particular conditions. Hence there are n(n–1)/2 degrees of freedom, i.e., numbers that must be assigned in order to specify the relations between these n particles. However, we find empirically that all the relations can be specified by just 3n numbers, namely, the x,y,z coordinates of each particle. Thus the number of pairs increases in proportion to n², whereas the positional degrees of freedom increases only in proportion to n. This represents a huge simplification, so we adopt the three-dimensional spatial model for the relations between particles. But obviously this model is not a logical necessity, it arises empirically from the (surprising) coherence of a large class of observational results.

In the case of relativity, the key facts are that (1) the inertial motions of material bodies have few enough degrees of freedom that they can be subsumed into our choice of coordinate systems, and (2) the motions of massless energy (such as pulses of light) conform to the very same set of coordinate systems. Energy is an inertial entity, so it fits into the same framework of inertial coordinate systems inferred for material objects.

Return to MathPages Main Menu