Continuity and the Void

Several early Greek philosophers, including Democritus, imagined the universe as consisting of a multitude of irreducible particles moving in an empty void.  On the other hand, Aristotle (c. 350 BC) denied the existence of a "void" (a region of space containing no substance), believing instead that the universe is filled continuously with substance.  In Book IV of Physica we find Aristotle's arguments against the existence of a "void".  He first addresses the claim that the compressibility of substances (such as air trapped inside a jar) implies the existence of empty space between the particles of air.  Certainly if air consists of irreducible particles, and if air is compressible, then there must be space between the particles.  However, Aristotle rejects atomism, and considers all substance to be continuous - meaning there are no finite irreducible entities.  From this point of view it's possible for a continuous substance to possess variable density, so the compressibility of air does not imply the existence of empty spaces.

Aristotle then argues against the idea that vacancy is a pre-condition for natural motion.  This position was held by the atomists, and again the cogency of this idea depends on the underlying atomistic view of the world.  From Aristotle's point of view, all motion results from the dual forces of levity and gravity, with the lighter elements (air, fire) tending upward and the heavier elements (earth, water) tending downward.  These elements simply change places, like an air bubble rising in water while the water fills in behind it.  He conceived of "levity" and "gravity" as buoyancy and anti-buoyancy, so that each element is the motive for the other elements' natural tendencies to move.  If we accept this view, then not only is vacancy not a pre-requisite for (natural) motion, it is actually incompatible with motion, because a substance located in a void, not surrounded or motivated by any adjoining substance of differing tendencies, has no reason to move at all.  (The illustrates how the outcome of arguments about the existence of the void is essentially built in to the basic world view that we adopt from the start.)

Next Aristotle considers "violent" motion, such as the motions of projectiles.  He points out that projectiles continue in motion even after they are no longer in contact with the hand that set them in motion, and he acknowledges only two possibilities to account for this.  The first is "circulatory thrust", by which he meant that the thrown object displaces the air in front of it, and this displaced air circulates around the object in a loop that ends up pushing the object and filling in from behind.  The second possibility is that the initial impulse (when the object was thrown) caused the whole column of air in front of the object to be pushed forward, and thereafter this moving shaft of air essentially pulls the object forward along with it.  In this case, presumably the column of air behind the object was also propelled forward.  This second "explanation" is not very convincing, because in order to account for the continued sideways motion of the object it relies on the continued sideways motion of another object, namely the air.  The first explanation is slightly more plausible, but of course from the modern perspective it's clear that this vortex cannot be imparting a net positive motive force to the object.  At best it can only reduce the drag.  But in Aristotle's mind the object's ability to remain in motion could only be explained in terms of this circulating external material.  We would regard the circulating air as a consequence of the object's motion, but Aristotle regarded it as the cause.  If we accept the premise that the circulating material around an object accounts for the object's tendency to remain in motion, then it does indeed follow that such motion would not be possible in a void.

Interestingly, at this point in his discussion, Aristotle digresses a little, and comes close to articulating Newton's first law of motion.  He points out that, in a void, neither of the two explanations for motion would be possible, "so nothing could go on moving unless it were carried", and then he adds

Nor (if it did move) could a reason be assigned why the projectile should ever stop - for why here more than there?  It must therefore either not move at all, or continue its movement without limit, unless some stronger force impedes it.

Compare this with Newton's statement that

Every body continues in its state of rest, or of uniform motion in a right line, unless it is compelled to change that state by forces impressed upon it.

However, despite the apparent similarity between these statements, it's clear from what follows that Aristotle was not really prepared to consider uniform motion in a straight line through the void.  He notes that the proponents of the void argue that objects move in a void because it offers no resistance, and he (rightly) points out that the void offers no resistance in any direction, so (he reasons) the direction of motion of an object in a void would be indeterminate.  Furthermore, he contends that the speed of an object in a void would necessarily be infinite.  This does indeed follow from his premise that the speed of an object is proportional to the motive force divided by the resistance of the medium through which it is passing.  Since the resistance of the void is zero, the speed of any moving object must be infinite. 

From our standpoint, it's tempting to simply conclude that although Aristotle's reasoning was correct here, his premises were wrong.  However, it's interesting to re-examine his ideas in the context of general relativity.  The modern account of motion is based on the concept of inertia, and the inertial paths (geodesics) through space and time are determined by the space-time metric, which also represents the components of the gravitational field.  According to classical general relativity, the metric field is a continuum, pervading all of space and time, and this field effectively determines not only the directions but also the speeds of inertial objects (for given initial conditions).  If we were to consider the possibility of a region devoid of the metric field, we would face conceptual problems similar to those that Aristotle encountered when he tried to imagine motion in a void.

One difficulty with the concept of co-existing continuous and mutually exclusive material substances is the problem of boundaries and cohesion.  We must first ask whether two adjacent continuous regions of pure substance will mix together.  If they do mix, then we must ask whether they combine to form a new continuous substance, or whether they simply form a mixture of small regions of the original pure substances.  If they split into small inter-mingled pure regions, what determines the size of these regions?  This depends on whether or not continuous substances possess a natural cohesion.  It is not clear that we can even define an intermediate degree of cohesion between the "parts" of a continuum without introducing an absolute scale, which would be inconsistent with the notion of continuity. 

The only intelligible possibilities for a continuous substance are either no cohesion at all or else perfect cohesion.  In the former case (no cohesion) we conclude that if two continuous substances mix, they must mix smoothly and continuously, which implies that there are no boundaries at all, but merely a single substance that may vary continuously from place to place.  Lacking coherence, there cannot exist any discrete regions of non-zero extent of distinct substances adjacent to each other.  This conflicts with the notion of a finite set of discretely distinct substances (e.g., Aristotle's earth, water, air, and fire).  The alternative (perfect cohesion) implies that the boundaries of continuous substances are inviolate.  They may stretch or bend in arbitrary ways, but the topologies of the boundaries must remain fixed.  Hence each contiguous region of a given substance constitutes a topologically unalterable entity. 

If we impose the requirement that the boundaries of these regions are each topologically equivalent to a sphere, then we essentially have a simple set of discrete entities, whose shapes and sizes may change (provided complementary changes occur in the surrounding entities) but which are otherwise quite similar to the atoms of Democritus.  Just as with Democritus' atoms, these regions may move about, and may interlock with each other in various ways, but each region retains its own inviolate irreducible identity.  On the other hand, we might choose not to require the boundaries to have the topologies of spheres.  For example, we could allow torus-shaped regions, or regions with any number of "handles", raising the possibility that two such regions could be permanently linked together.  We could even allow regions with more than one surface, so that it contains internal pockets of other substances.  It would be impossible for the trapped substances to ever escape from the enveloping substance, so we could never directly verify the existence of such internal pockets, although we might infer their existence from the density and compressibility of the enveloping region.

In any case, we find that the notion of discretely distinct continuous substances leads inevitably to some kind of absolute scale and/or irreducible structure (either metrical or topological), so the only non-atomic continuous structure consists of a single smoothly varying substance.  Since this substance comprises a single entity, and the only localized entities consist of properties of this substance.  Hence the movement of entities is really just the propagation of properties of this substance from place to place.  We could, of course, consider two kinds of motions, namely, motions of properties of the substance, and motions of the substance itself.  However, if we reject (as did Aristotle) the idea of an a priori plenum of space within which the substance resides, then it is not clear what it means for the all-pervasive continuous substance to "move".  The only dimensions recognized by Aristotle were measures of substantial things, and since we have been reduced to a single substance, he would be forced to argue that this substance cannot move.  It essentially constitutes space, and all the entities that we deal with are really just complexes of continuously varying properties of this space.

To further support this view, notice that Aristotle regarded spatial intervals only as the dimensions of some substance, rather than as distances between substances.  This is the crucial point.  The atomists who believed in the existence of the void naturally conceived of spatial intervals as distances between things, whereas Aristotle denied the existence of any intervals other than the lengths of substantial things (or some part of a substantial thing).  This is consistent with his rejection of the void (because a void, by Aristotle's definition has no extent), and it also implies that he must regard the quintessence as motionless, because there is no a priori reference against which to measure the "positions" of the substance.  The various points of the substance define their respective positions, and they obviously cannot move with respect to themselves.  It is only the continuously varying properties of the substance that can move (with respect to the substance).

Note that this argument relies on the idea of a continuum, because if a substance consisted of discrete particles with individual identities, and with the lattice taken as defining spatial relations, then we could imagine the particles re-arranging themselves into different configurations, in which case it would make sense to say that parts of the substance itself have "moved".  However, the local topology of a continuum is fixed.  We can apply any diffeomorphism, stretching and twisting the substance, but we cannot change the neighborhoods of the points.  (This relates back to the notion of cohesion.)  For a continuum, the most we can say is that there may be a property ("density") that is conserved locally, and if we associate such a property with the amount of substance per volume, then we could regard variations in this property as analogous to movements of the parts of a discrete substance, but this is really just an analogy, and an imperfect one, because it assumes discrete identities for different parts of a continuous density, which ultimately cannot be maintained.

To complete his argument against the existence of the void, Aristotle considers a wooden cube and its potential changes in position.  He says

Just as a cube displaces its own volume of water if immersed in it, so whatever the yielding medium may be, it must yield...  Now this yielding is impossible in vacuity, which is not a material entity at all, and one must suppose that the volume already there in the place before it was occupied must interpenetrate the equal volume of the intrusive cube when it enters, just as if the water should not make way for the cube but should permeate it all through.  But then the cube itself has its own volume equal to that of the vacancy that now permeates it, which volume, whether it be hot or cold or heavy or buoyant, is nevertheless different in its nature from all these qualities, even though it may not be separable from them (i.e., the volume, as such, of the wooden cube itself).  So that, even if this volume could be isolated from all these other qualities and be neither heavy nor buoyant [and neither hot nor cold], it would still embrace an equal measure of vacancy, and would coincide with a portion of "space" and "vacuity" equal to itself.  How then would the material volume of the cube differ from an equal volume of vacancy or space?  And if there could be two such coincident entities, why not any number you choose to name?

Why imagine a place for a body to go into, in addition to its own volume, if that volume, as such, has no physical properties?  For if another equal volume were to permeate it, it would make no difference.  From all this it is clear that there is no such thing as a self-existing void.

In essence, Aristotle's objection to the idea of unoccupied space (vacuity) as a thing with its own existence is that if we postulate such a thing, it would be possible to superimpose arbitrarily many such "things" and it would make no difference.  As Aristotle sees it, those who believe in the void are trying to define the absence of things as a thing, and he rejects the intelligibility of this on the grounds that it yields a non-unique result. There could be any number of co-existing voids.

There's an interesting echo of this line of reasoning in Einstein's famous "hole argument", which Einstein used to convince himself - for a time - that there could be no generally covariant field equations.  Suppose for a given system of space-time coordinates x there is a metric tensor field g(x) and a stress-energy tensor field T(x) that together satisfy the field equations F[g,T] = 0.  If this law is generally covariant, we can apply any diffeomorphic transformation δ to give a new set of coordinates δ(x) and the corresponding tensor fields δ(g) and δ(T) such that F[δ(g),δ(T)] = 0.  Now consider a bounded region H within which the stress-energy tensor is zero.  This region could be referred to as a void in Aristotle's terminology, because it is nothing but empty space.  Now suppose we choose a transformation δ such that δ(x) = x outside the region H, but δ(x) ¹ x inside the region H.  For any such transformation δ, we have δ(T) = T everywhere, because δ is the identity transformation outside the void region, whereas T (by stipulation) vanishes inside the void, and we have δ(0) = 0 for any δ.  Therefore, F[δ(g),T] is a solution of the field equations.  As Einstein saw it, this implies that for the same distribution T of stress-energy there are any number of distinct metric tensor fields δ(g) that satisfy the field equations inside the void, because we can choose δ arbitrarily inside the void.  The analogy to Aristotle's argument against the possibility of empty space, although not perfect, is nevertheless striking.

Of course, despite the ingenuity of Einstein's argument, he soon realized that his conclusion was incorrect, because the freedom to choose coordinates (up to diffeomorphism) represents another set of variables.  He was misled by suppressing that dependence in his symbolic notation.  We must actually write the field equations as F[g,T,x] = 0 and the transformed solution is F[δ(g),δ(T),δ(x)] = 0.  If, as before, we choose a transformation δ such that δ(T) = T, then we have F[δ(g),T,δ(x)] = 0, which is the same as the previous result, but the notation makes it clear that we cannot conclude there are two physically distinct metric fields inside the void.  We can only conclude that the field equations for the given T are satisfied by infinitely many pairs δ(g),δ(x) of coordinate system and metric field expressed in terms of those coordinates.  This was to be expected, because it's obvious that changing out coordinate system will require a corresponding change in the expression of the metric in terms of those coordinates.  This does not imply that the metric field is physically distinct, but merely that it is being described differently.

An even more compelling refutation of Einstein's original "hole argument" is simply to notice that, as he later wrote, "all our space-time verifications invariably amount to space-time coincidences... the introduction of a system of reference serves no other purpose than to facilitate the description of the totality of such coincidences".  (There is circumstantial evidence to suggest that Einstein got this idea from Erich Kretschmann, who wrote a paper on the subject in the summer of 1915.)  Now, any diffeomorphism of the coordinate system obviously maintains the same set of coincidences, in the same order, and with the same invariant proper times between them along any given physical path.  Einstein remarked in his 1916 paper that this "takes away from space and time the last remnant of physical objectivity", because it is ultimately only the intersections between tangible physical entities that constitute verifiable facts.  Empty space has no significance.  Again the parallel with Aristotle is striking.

However, Einstein was giving short shrift to the significance of space-time in his new theory, as shown by the important notion of proper time along paths between intersection events.  About seven years later, he wrote a famous essay entitled "Ether and the Theory of Relativity", in which he acknowledged that "To deny the ether is ultimately to assume that empty space has no physical qualities whatsoever.  The fundamental facts of mechanics do not harmonize with this view".  He continues

The metrical qualities of the continuum of space-time differ from one point to another... the recognition of the fact that empty space in its physical relation is neither homogeneous nor isotropic... finally disposed of the view that space is physically empty....  According to the general theory of relativity, space without ether is unthinkable...

It is seldom remarked that this, in a sense, vindicates the objections that Aristotle raised against the notion of the void.  The smoothly continuous quintessence that Aristotle's logic compels us to adopt is precisely in accord with the metric field of general relativity, which Einstein emphasizes is not physically empty, and can be regarded as an "ether".  Of course, Einstein hastened to add

But this ether may not be thought of as endowed with the quality characteristic of ponderable media, as consisting of parts which may be tracked through time.  The idea of motion may not be applied to it.

How Aristotle would have reacted to this caveat, we cannot say, but it is not manifestly in conflict with any of Aristotle's stated views.

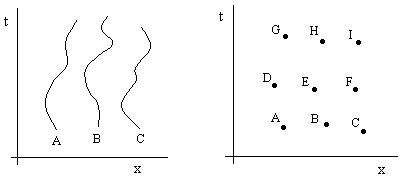
Can we conceive of an actual substantial medium to which the idea of motion cannot be applied?  The figures below help to illustrate the meaning of this restriction.

The figure on the left shows three of the constituent particles of a corporeal substance, and we observe these entities progressing through time with well-defined states of motion.  This can come about only if the parts of the substance have persistent identities, allowing them to be tracked from one time to another.  In contrast, the right hand figure shows several parts of a putative "substance", none of which has a persistent identity over time.  Each part exists only at a single place and time.  Indeed, this being the case, we may as well say that each one is a single place and time, i.e., an event in space-time, to use Minkowski's term.  According to this view it is the persistence of identity (through time) that distinguishes corporeal substances from the ether.  In this sense the ether and corporeal substances are completely different categories, as if (for example) the latter were just properties of the former.

Oddly enough, the modern understanding of elementary particles of matter entails a certain lack of persistent identity.  If the quantum wave functions of two electrons overlap significantly, then we can not track them individually through time.  They do not maintain individual identities, and there is a propensity for their identities to be "exchanged", making it impossible to assign a definite trajectory or state of motion to either particle on this scale.  Of course, on a larger scale, the wave functions of separate objects do not significantly overlap, so they acquire near perfectly persistent identities with definite states of motion.  We might imagine that the constituents of Einstein's ether are qualitatively similar to the constituents of ordinary corporeal substances, except that the quantum wave function of the each part of the ether extends over the entire interior of the lightcone of that part, so that the only restriction on its "state of motion" is that it is within the lightcone.

Return to MathPages Main Menu