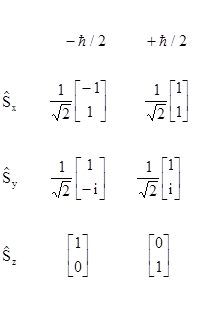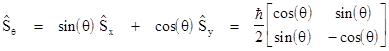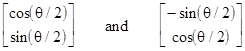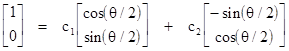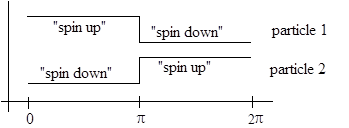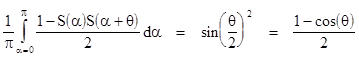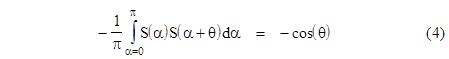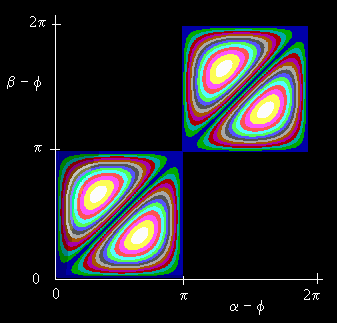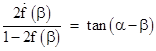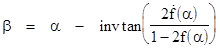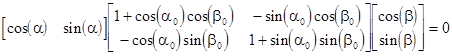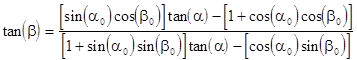Quantum Entanglement and Bell's Theorem

An overview of quantum entanglement and Bell’s inequality is presented in the note on Entangled Events. For a more detailed analysis, consider the quantum spin of an electron (or any spin-1/2 particle), which is always found to have either the value +h/2 or -h/2 in the direction of measurement, regardless of the direction we choose to measure. (This was first shown for silver atoms in the famous Stern-Gerlach experiment, and has subsequently been verified for many other kinds of particles.) Thus an electron manifests one of only two possible spin states, which we may call "spin up" and "spin down". It's convenient to represent these states as orthogonal unit vectors

In general an electron's spin state, Ψ, at any instant can be represented by a linear combination of those two possible observable states. The choice of a measurement direction is equivalent to choosing a "basis" for expressing the spin components of the state Ψ. For any particular basis we can express the state in the form

where c₁ and c₂ are complex constants. These constants encode the probability that the chosen measurement will yield either result. The probability is simply the norm of the respective coefficient. For example, if c₁ = a + ib and we let c₁* denote the complex conjugate, a - ib, then the probability of a measurement on this basis yielding "spin up" is equal to the norm, i.e., the product c₁*c₁ = a² + b². Likewise the probability of finding "spin down" on this basis is c₂*c₂. Since these are the only two possilities, we have

As always in quantum mechanics, each possible measurement basis is associated with an operator whose eigenvalues are the possible results of the respective measurement. For a given xyz basis of orthogonal space coordinates we can represent the three principle measurements (i.e., measurements along the three axes) by the matrices

The eigenvalues of the measurement operator corresponding to whichever measurement direction we choose determine the coefficients c₁ and c₂, which represent the probabilities of the possible outcomes.

To see how this works, suppose Ψ₁ is the initial state vector of the electron, and we decide to perform a spin measurement corresponding to a particular operator . The result is given by applying  to Ψ₁, using ordinary matrix multiplication, to give the new state vector Ψ₂ as shown below:

Since Ψ₂ is either pure "spin up" or pure "spin down" in the direction of measurement represented by , it follows that a subsequent measurement in the same direction must yield the same result, so Ψ₂ must be such that

for some constant λ (since state vectors are equivalent up to length). Thus the constant λ is an eigenvalue of the measurement operator , and Ψ₂ is the corresponding eigen-vector.

The outcome of (3) is unambiguous, because the eigenvector on the right side is the same as the eigenvector on the left side. However, since the arbitrary initial state Ψ₁ in (2) is not in general an eigenvector of , it can yield either of the eigenvectors of . This reveals the probabilistic aspect of quantum mechanics.

The eigenvectors of  constitute a basis for the space of possible state vectors, so Ψ₁ can be expressed as a linear combination of those eigenvectors. If we let Ψ₂ and Ψ_2' denote the eigenvectors, then we can express Ψ₁ as

Again, the norm of each complex coefficient gives the probability that  applied to Ψ₁

will lead to the respective eigenstate.

For the three principle direction spin operators , , and  presented above, the eigenvectors corresponding to +h/2 or -h/2 are as shown below:

Each pair of eigenvectors constitutes a basis for the state space, so we can express the electron's state vector as a linear combination of the basis vectors for the desired measurement, and the coefficients give the probability of that measurement yielding either "spin up" or "spin down".  We can think of these probabilities as the projections of the initial state vector onto the orthogonal axes of the chosen measurement basis.

Of course, we aren't restricted to measurements along one of the principle axes. We can measure the spin of the electron along any spatial axis, and each such measurement is represented by an operator. We also note that these directions are purely relative to the state of the particle in question. To illustrate, suppose a stream of electrons is moving along the y axis and we perform spin measurements on these particles in the z direction, which establishes the z component of the particle's spin vector. If we filter out all those particles with "spin down" in the z direction, we are left with a stream of particles all having "spin up" in the z direction. Now suppose we perform a spin measurement on the remaining particles along the direction in the xz plane at an angle θ with the positive z axis. In accord with the interpretation of probabilities as the projections of the state vector onto the basis axes, we infer that the measurement operator for spin in this direction is given by the projections of the x and z operators

Naturally the eigenvalues of this operator are +h/2 and -h/2, and it's easy to show that the corresponding eigenvectors are

respectively. Each particle subjected to this measurement will have the initial state vector indicating "spin up" in the z direction, and we can express that initial vector as a linear combination of these basis vectors

which implies that the coefficients are c₁ = cos(θ/2) and c₂ = -sin(θ/2). Consequently, the probabilities of "spin up" and "spin down" for a measurement of such a particle along the θ direction are cos(θ/2)² and sin(θ/2)² respectively.

These quantum mechanical predictions (which have been well supported by experiment) have some remarkable implications. In the preceding example we established the initial state vector by performing a measurement in the z direction and considering only particles that yielded "spin up" in that direction. Then we subsequently performed a measurement at an angle θ relative to the positive z direction, and the probabilities of the outcomes were found to be a function of the angle θ between those two measurements. An essentially equivalent experiment can be performed by examining the spins of two spin-1/2 particles emitted in opposite directions from the decay of a singlet state with zero total spin. In such a case conservation of angular momentum requires that the spin state vectors of the individual particles are precisely opposite, so if we measure the spin of one of these particles along a certain direction and find "spin up" in that direction, then the other particle must have pure "spin down" in that direction. Thus, by measuring the spin of one particle and reducing its state vector to one of the eigenvectors of the chosen measurement basis, we automatically "collapse the wavefunction" of the other particle onto this same basis.

At first this process may not seem very mysterious, since it's easy to imagine that the two coupled particles are "programmed" with opposite spins, such that they will always give opposite results when measured along any given direction. However, a careful analysis of the quantum mechanical predictions for all possible combinations of measurement angles reveals the need for a profound shift in the classical view of the world.

If the measurement of one particle along a fixed direction (in the xz plane) yields "spin down", then the other particle is purely "spin up" in that direction. Consequently if we perform a measurement on the other particle along a direction at an angle of θ from the first measurement, we've already seen that the probability of "spin up" is cos(θ/2)² and the probability of spin down in sin(θ/2)². In a similar way we can show that if the measurement of the first particle yields "spin up", then the other particle is purely "spin down" along that direction, and a measurement of that other particle along a direction at an angle θ relative to the first will yield "spin up" with probability sin(θ/2)² and spin down with probability cos(θ/2)².

Hence the probability that the measurements of these two particles at angles differing by θ will both give the same result (both up or both down) is sin(θ/2)², and the probability that they will yield opposite results (one up and one down) is cos(θ/2)². The angle θ between the two measurements can be expressed as α - β where α is the angle of the measurement performed on one of the particles and β is the angle of the measurement performed on the other. The two particles emitted from a singlet state are said to be entangled, because regardless of how far apart they travel before the spin measurements are made, the joint results will exhibit these joint probabilities.

From a classical standpoint we would imagine that each particle emerges from the singlet state with, in effect, a set of pre-programmed instructions for what spin to exhibit at each possible angle of measurement, or at least what the probability of each result should be. The usual approach to analyzing these phenomena classically is to stipulate that a particle's pre-programmed instructions for responding to a measurement at a given angle must be definite and unambiguous (rather than probabilistic) because we classically regard the two measurement angles as independent, which implies that the measurement on the "other" particle could be at the same angle as our measurement of this particle, and the particles must give opposite results in that case. Likewise the measurement on the "other" particle could be 180 degrees away from our measurement of this particle, and the particles must give equal results in that case. Of course, the individual measurements can each be either "spin up" or "spin down" in both of these cases, so in principle they could still be probabilistic tendancies, but classically we have no way of ensuring perfect correlation (or perfect anti-correlation) of the joint results of spacelike separated events other than by definitely pre-programming the spins of each particle for each possible measurement angle.

From this assumption it follows that the instructions to one particle are just an inverted copy of the instructions to the coupled particle. In other words, for each measurement angle from 0 to 2π the pre-programmed response to a spin measurement for one particle is the opposite of the pre-programmed response of the other particle at that angle. Furthermore, since we have perfect correlation if our measurements are at angles that differ by 180 degrees, it follows that the pre-programmed instructions for each particle are individually anti-symmetric at a phase angle of 180 degrees. For example, if a particle's programmed response for a measurement at angle α is "spin up", then the programmed response of that same particle for a measurement at angle α + π must be "spin down". Hence we can fully specify the instructions to both particles by simply specifying the instructions to one of the particles for measurement angles ranging from 0 to π.

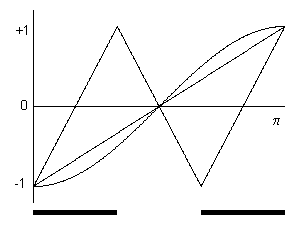
The simplest function that satisfies the conditions stated so far is constant "spin up" over the range from 0 to π for one of the particles. This gives the total "response programs" of both particles shown below:

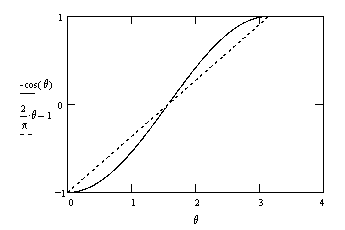
Naturally we can take the absolute orientation of this profile as arbitrary relative to our measurements. Unfortunately this simple profile doesn't give the correct (quantum mechanical) joint correlations for measurement angles that differ by amounts other than 0 or 180 degrees. If we define the correlation exhibited by the measurements results of a set of particle pairs as the number of agreements minus the number of disagreements, all divided by the total number of pairs, then it's easy to see that the correlation yielded by pairs with the above instruction profiles (oriented randomly) varies linearly as a function of the difference between the measurement angles. The correlation is –1 if the angles differ absolutely by 0, the correlation is zero if the angles differ by π/2 (90 degrees), and the correlation is +1 if the angles differ by π (180 degrees). In general, for measurement angles differing by θ, the correlation is C(θ) = (2/π)|θ| - 1. In contrast, since the quantum mechanical predictions for agreement and disagreement are sin(θ/2)² and cos(θ/2)² respectively, the quantum mechanical prediction for the correlation is

A plot of the simple linear correlation profile and the quantum mechanical profile is shown below.

These profiles agree only for measurements differing by 0, π/2, and π. For all other cases the simple pre-programmed linear model fails to match the predictions of quantum mechanics - which have been amply verified by experiments. This raises the interesting question of whether any pre-programmed response profile can reproduce the predictions of quantum mechanics (and the experimental results). Suppose each particle is programmed with a more complicated profile of responses as a function of the measurement angle. In general we could partition the angular range from 0 to π into n arbitrary segments, alternating between "spin up" and "spin down". Together with the perfect correlation and anti-correlation requirements at angluar differences of 0 and π, this suffices to determine the putative response profiles of both particles over the entire range from 0 to 2π. Letting α S(α) denote the spin result (+1 for up and -1 for down) at the measurement angle α for one of the particles, and letting s(α) denote the spin result of the other particle, we have S(α) = -s(α) and S(α) = -S(α+π). The two results agree for measurement angles α and β if S(α)s(β) = +1, and they disagree if S(α)s(β) = -1. The absolute values of α and β are taken to be arbitrary, so the probability of agreement for all cases where b - α = θ for any fixed θ is given by integrating the quantity

from α = 0 to π. (The result is symmetrical for α - β = θ, and for the range from π to 2π.) Therefore, equating this with the quantum mechanical result, we must have

which implies

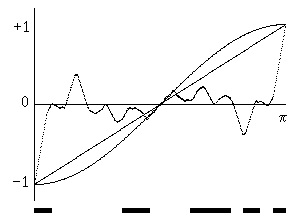
This is just the correlation between the two measurements. If S(α) = +1 on the entire interval from α = 0 to π (and therefore S(α) = -1 for all α from π to 2π), the left hand side can be split into two integrals, one extending from α = 0 to π-θ with an argument of +1, and the other from α = π - θ to π with an argument of –1. Hence the left side reduces to (2/π)θ - 1, as we saw earlier, and this does not match the quantum mechanical prediction. In particular, we note that the rate of change of the quantum correlation near θ = 0 is zero, whereas the rate of change of the correlation for based on our simple S function has a positive slope at θ = 0. This is because the increase in correlation is proportional to the increase in θ, arising from the transition at α = π - θ. Clearly this rules out every fixed S function, because if any more transitions are added to the pre-programmed instructions, the slope of the resulting correlation will increase proportionately. To illustrate, consider the S function and the resulting correlation function shown below:

The solid bars at the bottom signify the angular regions where "spin up" has been pre-programmed for this particle. Since there are three times as many transitions, the slope of correlation versus angle is three times as great as in the basic case considered previously. This is true regardless of how these transitions are distributed. For another example, consider the S function and resulting correlation shown below:

This S function has nine transitions, so the initial slope is nine times as great as the baseline case. We're forced to conclude that no pre-programmed set of results for the range of possible measurement angles can possibly reproduce the quantum mechanical predictions (and experimental results). Equation (4) does have the formal solution

but of course this S function isn't restricted to the discrete values +1 and –1, so it can't be directly interpreted as a spin indicator.

Many treatments of quantum entanglement discuss "hidden variables", and they derive inequalities involving the correlations as functions of these putative variables. In a sense, these variables are redundant, because the essence of the so-called "local realistic" premise is that each particle emerges from the singlet state with definte instructions for the spin it will exhibit for each possible measurement angle. This implies that the only relevant free variable is the reference orientation, since the instruction profile can be oriented in any direction (relative to the measurements) with uniformly distributed probability. Integrating the product of spins over the entire angular range with a fixed difference angle must yield the correlation of the two spin measurements.

It might be argued that we need not assume any single particle exhibits the quantum mechanical probabilities, because these probabilities can only be evaluated by performing multiple measurements, so we might imagine that it's necessary to evaluate the results over a sequence of particle pairs, rather than just a single pair. Moreover, we might think that this sequence could possess "memory", making the results of successive pairs dependent. However, in principle we could prepare a large number of particle pairs in an identical way, in spacelike-separated locations, and perform measurements on the pairs independently (again based on the naive conventional concept of local realism). According to quantum mechanics we would still expect the combined results to satisfy the same correlations. This implies that each particle pair must embody the overall propensities that we expect to find manifested in multiple trials.

Nevertheless, it's worthwhile to review the traditional derivation of Bell's inequality based on the premise that each particle emerging from the singlet state possesses a definite spin as a function of the measurement angle and some "hidden variable" m associated with that pair. We assume an arbitrary probability density function d(m), which gives the probability density for any given pair of particles being produced with that value of m. The observed spins of the two particles are denoted by S(α,m) and s(β,m), where α and β are the angles of the respective measurements. As before, the perfect anti-correlation of the two particles measured at the same angle (according to quantum mechanics) implies that S(α,m) = -s(α,m). (In our previous discussion the implicit "hidden variable" was simply the absolute reference angle for the measurements, with a uniform probability density over the range from m = 0 to 2π, but we can argue more generally for any hidden variable with any probability density over any range.)

Now we consider the pairwise spin correlations for three different angles, α, β, and f. If one member of each coupled pair of particles has its spin measured at the angle a and the other is measured at the angle f, the correlation between the measurements is given by

where the integral is evaluated over the full range of m. Likewise if one particle is measured at β and the other at f, the correlation is

Taking the difference between these two, we have

Since every spin value is either +1 or -1, it follows that S(α,m)² = 1, so the value of S(β,m) in this expression can be written as S(α,m)² S(β,m), and we can then factor out from the square brackets to give

Now we take the absolute value of both sides, and make use of the obvious fact that the absolute value of a definite integral of a function is less than or equal to the integral of the absolute value of the function, we have the inequality

Conventionally, a probability density function always has a non-negative real value, so we stipulate that d(m) is non-negative. Also, since the product S(α,m) S(β,m) is always +1 or –1, the quantity in the square brackets is always either +2 or 0. The leading factors, s(f,m) S(a,m), always equal +1 or –1, so they determine the sign of the integrand, which is discarded by taking the absolute value. Hence the expression reduces to

Replacing S(β,m) by -s(β,m), and splitting the integral into two parts, give

The first integral is simply 1, since d(m) is a probability density function, and the second integral is the correlation for two entangled particles measured at the angles α and β. Hence we can subtract this from both sides to give Bell's inequality

We can evaluate the left hand function assuming the quantum mechanical correlation C(x,y) = -cos(x-y). This gives |cos(α-f) - cos(β-f)| + cos(α-β), which is shown in the figure below. The colored regions represent that cases where this quantity exceeds 1, and therefore violates the above inequality. The maximum violations occur in the four white regions, where the function attains the value of about 1.5.

A different approach to analyzing quantum entanglement is to assume that each particle is pre-programmed not with a definite result for each measurement angle, but with a probability of yielding specific results. Needless to say, this model will be incompatible with the premise of independence of measurement angles, because a probabilistic model can't automatically enforce the perfect correlations and anti-correlations predicted by quantum mechanics at θ = 0 and π. Still, the previous discussion has shown that the naive premises of "local realism and free choice" are untenable anyway, so it's worthwhile to examine a probabilistic scheme.

Thus we imagine that the first particle contains a function f(α) that represents the probability of' yielding spin up for the measurement angle α. Likewise the second particle is programmed with the function g(β) that represents the probability of yielding "spin up" for the measurement angle β. In these terms we can express the probabilities of agreement and disagreement as

If we double the "disagree" equation and subtract 1 from both sides we get

Incidentally, if we expand the right-hand side using the trigonometric angle addition formula, we get the interesting expression

which could be regarded as an "inner product" of vectors with the components of the form sin(α), cos(α), and 1 - 2f(α).

Returning to the original "disagree" equation, if we assume the functions f and g individually possess derivatives, and if α and β are independent variables (as is classically the case for two freely chosen measurement angles), we can take the partial derivative with respect to β at any constant a to give

Solving for 1 - 2f(α), substituting into equation (5), and re-arranging terms gives

Similarly we can derive the relation

It's interesting that the expressions on the left side of these equations are formally the same as the queing theory "transition rates" of the functions 2g and 2f if we identify these functions with the state probabilities and the arguments α and β with the model time.

In any case, notice that these equations theoretically imply that each of the two entangled particles contains enough information to enable someone to compute the measurement angle at the other particle. For example, the second equation can be solved for β to give

Hence, assuming the particle contains the complete function f, and assuming this function possesses derivatives, it follows that the measurement angle β at the other particle is a deterministic function of the measurement angle a at this particle. This contradicts the premise that α and β are independent variables, so the only possible conclusion is that one or more of our basic assumptions were wrong. One questionable assumption was that not only does each particle "contain" its respective function (f or g), but that these functions are differentiable. This need not be the case. Continuous but nowhere-differentiable functions are well-known in mathematics, and we could postulate that f and g are such functions.

On the other hand, if we rule out such exotic functions, it seems that the only remaining possibility is that, even though we may believe we are free to choose the two separate measurement angles "freely" and independently, they are actually deterministically linked. In other words, not only are the particles entangled, but so are our "free" choices of measurement bases for those particles. This analysis suggests a much more deterministic universe than is commonly conceived, regardless of whether it's possible to extract the information about f and its derivative from the particle. (These "free" choices may even be spacelike separated, but of course this does not imply any violation of special relativity, because it is only necessary to assume that the choice events share a common event in their causal pasts, which is always the case provided we are willing to go back far enough.)

Suppose we differentiate equation (6) again with respect to β at constant α to give

The left hand side is equal to (1-2f)(1-2g), so we can make this substitution, cancel the factor of (1-2f), and re-arrange terms to arrive at

This has the particular solution g(β) = 1/2, and we can add this to the homogeneous solution to give the total general solution

Since this function signifies the probability of "spin up", we expect it to be real-valued and in the range from 0 to 1. Hence we can set C₁ = C₂ = 1/4 to give

Applying the same analysis to f(α) and setting C₁ = C₂ = -1/4 gives

If we then substitute these expressions back into the original "agree" and "disagree" formulas, we find that in both cases they reduce to

Comparing this with the trigonometric identity

we see that it is not generally satisfied unless α or β is a multiple of π, in which case it is trivially satisfied. One way around this impasse is to postulate slightly more general functions for f and g, namely

where α₀ and β₀ are constant phase angles for a given pair of particles. Substituting these functions into the basic "agree" and "disagree" equations gives the single condition

The can also be expressed as a null line element

where the determinant of the coefficient matrix is 1 + cos(α₀ -  β₀). It can also be expressed in the form of a Mobius transformation between the tangents of α and β as follows

The similarity parameterof the transformation is 1 - cos(α₀ -  β₀), whereas the normalized trace is tan((α₀ - β₀)/2).

Return to MathPages Main Menu