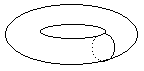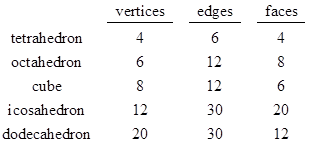The Tetratorus and Other Multi-Layered Polyhedra

We usually regard an ordinary polyhedron as a three-dimensional solid with a single-layered two-dimensional surface. On this basis we can easily count the number of vertices, edges, and faces, and compute the Euler characteristic of the surface

It can be shown that any simply-connected closed 2-dimensional surface (i.e., a surface that has the same topology as a sphere) has an Euler characteristic of 2. This applies to all the most familiar polyhedra, such as the Platonic and Archimedian solids, and many others as well. (Apparently Descartes was the first person to notice the simple numerical fact that V – E + F = 2 for all these solid shapes, which is remarkable, considering how numero-logically inclined the ancient Pythagoreans were.)

To be a bit more rigorous about the meaning of "simply-connected", note that a surface S is defined to be "connected" if any pair of its points can be joined by a continuous curve lying entirely within the surface. Further, a surface is said to be "simply-connected" if any closed curve C on the surface divides the surface into two distinct regions, each of which is internally "connected" in the sense just described, and such that any continuous curve which joins a point in one of those regions to a point in the other must cross the closed curve C.

Another, somewhat less formal, way of characterizing a simply-connected surface is to say that any closed curve on such a surface can be "shrunk" continuously to a point, without ever departing the surface. We mentioned previously that the surface of a sphere is simply-connected, and obviously any circle drawn on a sphere can be shrunk to a point. On the other hand, the surface of a torus (a doughnut) is not simply connected, because we can draw a closed curve around a torus shape in such a way that the curve cannot be shrunk any further. Also, from our previous definition, we can see that some closed curves C on the surface of a torus do not bisect the surface into disconnected parts, as shown below.

In this sense, the torus is topologically distinct from the surface of a sphere, and consequently it has a different Euler characteristic. If we triangulate the surface of a torus (in any way we like) and count the number of edges, faces, and vertices, we find that the Euler characteristic is 0.

Incidentally, the Euler characteristic of a surface is directly related to the total Gaussian curvature of that surface. Specifically, the Gauss-Bonnet theorem states that for any compact oriented two-dimensional Riemannian manifold S, if we let K denote the Gaussian curvature as a function of position on the manifold, then we have

In other words, the integral of the Gaussian curvature over the entire area of the manifold equals 2π times the Euler characteristic. For example, the Gaussian curvature of a sphere of radius r is a constant 1/r², so the integral of this over the entire surface of the sphere is simple 1/r² times the total surface area A of the sphere. Now, since e(S) = 2 for a sphere, we must have

and therefore the surface area of a sphere must be 4πr², which of course it is. Compare this with the reasoning that Archimedes originally used to deduce the surface area of a sphere (see the note Archimedes on Spheres and Cylinders). The Gauss-Bonnet theorem is a truly beautiful fact, relating a metrical property (curvature) to a purely topological property (the Euler characteristic). Notice that this theorem can be applied to polyhedra as well, if we agree to assign the appropriate amount of "curvature" to the vertices (since there is no curvature on any face or edge).

It follows from this theorem that the "net" Gaussian curvature of a torus is zero, so it's possible to define a perfectly flat metric globally over the entire surface of a torus. On the other hand, it's obviously not possible to define a flat metric globally on a sphere, or on any surface homeomorphic to a sphere. This is true even though the Gaussian curvature on the surface of a polyhedron is zero at all but a finite number of points (the vertices).

But this leads us to an interesting question, namely, whether it is possible to "wrap" a completely flat closed surface (i.e., a torus) onto the surface of a convex polyhedron if we allow multi-layered surfaces. For example, if we create a surface out of squares, we must have a certainly number of squares meeting at each vertex, and each square represents a right angle. Now, for a single-layered flat surface there must be four right angles meeting at each vertex, whereas for a single-layered cube there are only three right angles meeting at each vertex. However, our surface need not be connected after just a single loop around a given vertex. Indeed we can imagine a "spiral staircase" consisting of a surface that circles a vertex many times before re-connecting with the original sheet. Of course, if this two-dimensional surface is embedded in three-dimensional space we won't be able to re-connect without self-intersecting, but this is just a restriction related to the embedding in three-dimensional space, similar to the fact that a "Klein bottle can't be realized in three-dimensional space without self-intersecting, whereas it can be realized in four-dimensional space. By the same token, we can imagine a sheet circling a vertex arbitrarily many times before finally re-connecting to the original sheet.

The underlying "shape" of this multi-layered manifold will still depend on the angular travel around the vertex that brings us back to the same location in the manifold, but now we can allow multiples of the basic angular requirements. If we must travel through some multiple of four right angles to get back where we started, then we can imagine that these sheets are molded in a flat shape, whereas if we must travel through a multiple of three right angles to get back where we started, we can imagine that that this surface is molded in the shape of a corner of a cube. But what if the total angular travel around a vertex is a multiple of both three right angles and four right angles, i.e., what if it is a multiple of 12 right angles? In that case we have a multi-sheeted surface that can be interpreted as either flat or as the vertex of a convex solid, i.e., as a point with non-zero curvature.

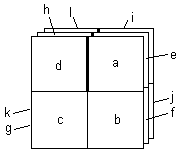
Actually it isn't difficult to construct this surface out of paper. Just cut three identical squares, and draw two perpendicular lines though the center of each square so that each is divided into four faces. Then cut along one of those lines from one edge to the center, and tape the squares together in a spiral pattern, as indicated below.

The cuts in the three original squares of paper are along the thick vertical lines, and the right-hand edge of "d" is connected to the left-hand edge of "e" (which is underneath "a"). Similarly, the edge of "h" is connected to the edge of "i". Lastly, after making three complete circuits around the central vertex, the edge of "l" on the bottom sheet is connected to the left-hand edge of "a" on the top sheet. This last connection obviously can't be achieved in three dimensions without the surface intersecting itself, but just as with the Klein bottle we are free to imagine an embedding in a higher dimensional space that allows us to adjoin all the edges as described. As an alternative, we can neglect the embedding entirely, and simply conceive of this as a two-dimensional surface with its own intrinsic properties.

The interesting thing about this surface is that it "works" as a three-layered flat plane, bit it also works as a four-layered corner of a cube. To see this, it's helpful to first crease the sheets along the orthogonal lines, and then simply "wind up" the faces around the vertex, so that three (rather than four) square faces meet at the vertex. Notice that the intrinsic connections between all the faces of this "wound up" version are identical to the connections of the "flat" version, including the alignment of the adjoining edges of the "l" and "a" faces. In effect, we began with a three-layered flat surface, but this can also be interpreted as a four-layered surface that follows the shape of a cubical vertex. If we consider the surface "modulo the cube", we see that it has intrinsic curvature. If we consider the surface modulo the "flat" arrangement we group the faces into the four equivalence classes

whereas if we consider the surface modulo the curved arrangement we group the faces into the three equivalence classes

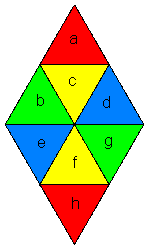
Of course, neither of these interpretations yields a closed surface. This raises the interesting question of whether it's possible to devise a closed surface that can be interpreted equally well as flat or curved, depending on which "shape modulus" we select. It turns out that it is possible. The simplest example is based on the tetrahedron. To construct a model of this, cut out a piece of paper in the diamond shape shown below, comprised of 8 equilateral triangles

Now make a cut along the boundary between regions "f" and "g", and wind up the surface around the central point, so that three triangles meet at that point. This results in a two-layered tetrahedron, and the four faces correspond to the four colors on the above figure. Thus the eight original triangles are grouped into the four equivalence classes

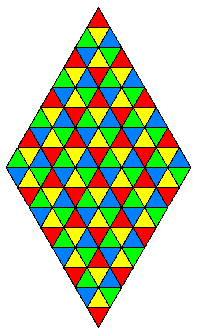
The important point to notice is that this arrangement brings all the edges into alignment in a way that is perfectly consistent with a flat arrangement of the faces. Note that if we take many copies of the above diamond figure and set them side-by-side, we have the doubly-periodic tiling illustrated below

This shows how all the 8 regions of the original diamond must be interconnected to form a torus, which then is given by identifying the upper left boundary of the original diamond with the lower right, and identifying the upper right with the lower left. In this flat interpretation we have only a single layer, so we have the 8 equivalence classes

The connections between these eight triangles are identical, whether we view them as comprising a single-layered torus or a two-layered tetrahedron. Of course, the curvature of the latter arises only when we reduce the surface modulo the tetrahedron. By the way, notice that we have the extrinsic arrangement of layers (i.e., "inner" and "outer") indicated below

We can make either of these sets the "inner" surfaces and the other the "outer" surfaces, depending on how we choose to "wind up" the faces around the original central vertex.

Another way of constructing the "tetratorus" is to begin with the same 8-part diamond shaped piece of paper as above, but this time make a cut along the boundary between regions "d" and "g". This results in the same intrinsic arrangement as before, but the extrinsic knotting of the surfaces is different. With this construction we get the "outer\inner" partition

The actual extrinsic distinction between these two arrangements is clarified by considering the two graphs of the tetrahedron shown below.

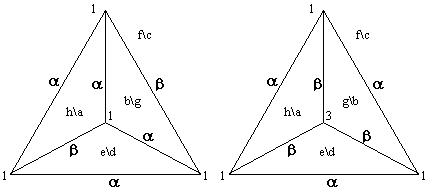
Each edge can be regarded as a permutation of two elements, since we must decide for each edge how to map the two sheets (inner and outer) of one face to the two sheets of the adjoining face. In the diagrams above we have used the Greek letters α and β to denote the identity permutation [12] and the transposition [21] respectively. Now, for each vertex to be "flat", it is necessary that we must circle around it through 6 equilateral triangles to get back where we started, which means that a single circuit around the vertex (as seen modulo the tetrahedron) must give a net transposition, so we must have an odd number of [21] edges meeting at each vertex.

Indeed, for the first arrangement (on the left above) there are two edges carrying the [21] (β) permutation, and exactly one of these meets each vertex. On the other hand, for the second arrangement (on the right above) we have swapped the outer\inner positions of the congruent faces "b" and "g", which implies that every α on the edge of this face becomes β, and vice versa. This still works, as we now have three transpositions meeting at one vertex, and one transposition at each of the remaining vertices, i.e., we still have an odd number of β edges meeting at each vertex. From an intrinsic standpoint these two surfaces are equivalent, but they are knotted differently in the embedding space. To see this, observe that it's possible in the first arrangement to make a complete loop around all the outer (or all the inner) faces without ever crossing the same edge twice and always remaining on the same level. In contrast, this is not possible with the second arrangement.

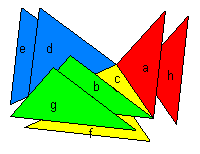
An exploded view of the tetratorus is shown below

Depending on which of the embeddings we choose, we can make the appropriate identifications of edges so that the surface of the two-layered tetrahedron has the same connectivity as the flat torroidal surface. For example, to give the embedding corresponding to the right hand graph in the preceding schematics we would make the natural connections of the outer layers to the outer base (yellow) triangle, and then make transposing identifications along the remaining three edges. In other words, connect g,e, and h with f, and then make the connections gd,be and ga,bh and ae,dh.

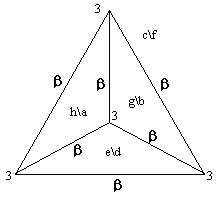
One other possible embedding arrangement now immediately presents itself. If we swap the outer\inner positions of the congruent faces "c" and "f" in the right hand graph above, we produce the graph shown below, which must have transpositions for all 6 of its edges.

In this case we have three β edges meeting at each vertex, and this embedding is obviously distinct from each of the other two, because we can't travel from any face to any other face without switching layers. Nevertheless, all three of these multi-layered tetrahedral surfaces are intrinsically equivalent, not only to each other, but also to the single-layered torus.

We could regard the two-layered surface of this figure as a Riemann surface from the field of complex functions, and each vertex as a branch point. Recall that the function f(z) = z^r has a branch point at z = 0, and if the exponent r is a rational number, so that r = m/n for coprime integers m and n, then the Riemann surface has n layers that spiral around the branch point at the original. We must circle the origin n times to get back to our starting point. With n = 2 (i.e., for r equal to a half-integer) this means that the Riemann surface for the function z^r has two layers, and we must circle the origin twice to get back to our starting point. This is obviously very similar to the two-layered surface of the tetratorus. This leads us to consider whether there exists a complex function on the surface of a sphere (or perhaps the plane) with four branch points, each of order 2. The Riemann surface for such a function would have the topology of the tetratorus. Consider the function

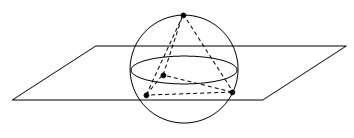
This function, evaluated over the extended complex plane, has four branch points, counting the “point at infinity”, which we expected to need when mapping stereographically from the sphere to the plane, as depicted in the figure below.

The dashed lines represent the edges of a tetrahedron inscribed in a sphere. With a suitable choice of scaling and orientation, the lower three vertices can be mapped stereographically from the “North pole” to the three cube roots of 1 in the complex plain. The upper vertex then maps to the point at infinity in the complex plain. The function f(z) noted above has a 2-sheeted Riemann surface with branch points of order 2 at each vertex. It’s well known that this surface has the topology of a torus, in agreement with our construction of the tetratorus.

Recall that in order to make a surface that corresponds to both a multi-layered plane and a multi-layered cube we needed the flat arrangement to have three layers while the cubical arrangement had four layers. This was necessary in order for a circuit around a vertex to be a multiple both of 2π and of (3/2)π. In contrast, to make a tetratorus we found that the flat surface was single-layered and the tetrahedron was two-layered. In general it's not difficult to see what the requirements are for the various regular polyhedra. We have the basic attributes

and the Euler characteristic is V − (E − F). Also, the number of vertices doesn't change when we transform the surface from flat to curved, so the total number of vertices will be jV if we have j layers in the flat interpretation. On the other hand, the numbers of edges and faces is proportional to the number of layers we have in the polyhedral interpretation. Letting k denote this number, we see that the intrinsic Euler characteristic is jV − k(E − F), and we need to make this vanish. The minimal solutions for each type of solid are

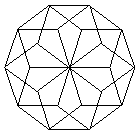
For example, here's an image of a "flat" vertex where pentagons meet.

It's easy to see that these are the numbers of layers necessary, in each case, to arrange around a single vertex so that it can be interpreted as a multiple of a flat surface and as a multiple of the vertex of the respective polyhedron. It would be interesting to know if complete closed surfaces equivalent to multi-layered tori can be constructed in cases beyond the tetrahedron. In each case it would be a matter of identifying the arrangement(s) of permutations of k elements that would yield the appropriate layer changes for each edge, in such a way that the entire closed surface "works" as both a flat surface and (modulo the polyhedron) a curved surface. This involves considerations that are closely related to those discussed in the note on Permutation Loops.

Return to MathPages Main Menu