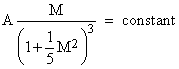Normal Shock Waves

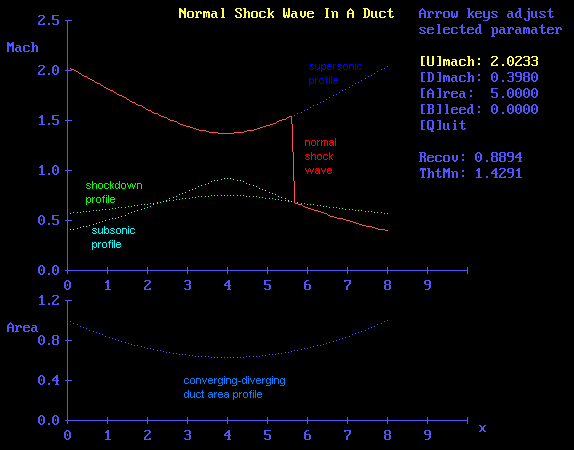
Under certain conditions it is possible to establish a standing normal shock wave in a duct. The location of the shockwave depends on the variation in the cross-sectional flow area of the duct, as well as on the upstream and downstream boundary conditions.

In general, one-dimensional isentropic flow of a perfect gas is characterized by a constant value of the parameter

where A is the cross-sectional flow area, M is the Mach number (i.e., the ratio of the flow velocity to the speed of sound in the gas), and we have assumed a ratio of specific heats (usually denoted by γ) equal to 1.4, which is the characteristic value for air. This relation holds for both subsonic and supersonic flow. Thus, given the area profile of a duct, and the (supersonic) upstream Mach number, we can compute the Mach number at every point in the duct, based on the isentropic flow assumption. Likewise, given the (subsonic) downstream Mach number, we can compute the Mach at every point in the duct, again based on the assumption of isentropic flow. Ordinarily these two profiles will not intersect, proving that we cannot maintain those upstream and downstream conditions with purely isentropic flow. Consequently, at some point in the duct there must be a shock wave.

The Mach number M_d downstream of a normal shock is related to the Mach number M_u upstream of the shock (still assuming γ = 1.4) by the equation

Therefore, at each point in the duct we can compute the "shock down profile", which represents the Mach number that would exist just downstream of a normal shock from the supersonic Mach profile. The point at which this shock down profile intersects with the isentropic downstream profile is where the shock wave must occur. This is illustrated for a generic converging-diverging duct in the figure below.

The sensitivity of the shock position to changes in the duct area profile and the upstream and downstream boundary conditions can easily be inferred from these simple relations.

Return to MathPages Main Menu