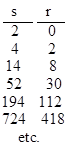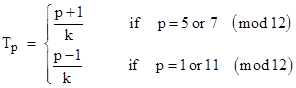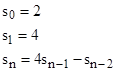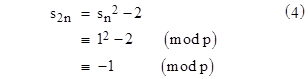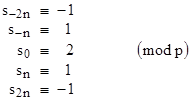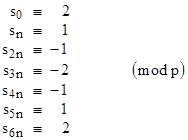Some Properties of the Lucas Sequence

The second-order recurrence

arises in many different situations, such as in the sequence of "Lucas Numbers" used in primality tests of Mersenne numbers, and in Heronian triangles, and continued fractions for √3, and in general anything that involves the Pell equation x² – 3y² = 4. With the "natural" initial values s₀ = 2 and s₁ = 4, we have the sequence

This sequence comprises the integer values of s that satisfy the Pellian equation

with the corresponding values of r listed below

I referred to (2) as "Pellian" rather than a Pell equation proper, because the right hand side is not unity. However, given any solution of the Pellian equation we can obviously construct others by simple multiplication of similar quadratic forms. For example, suppose we have integers s,r that represent a solution of s² – 3r² = 4. Then for any of the infinitely many integer pairs u,v that satisfy the Pell equation u² – 3v² = 1 we have

Now, the minimal non-trivial solution of u² – 3v² = 1 is (2,1), so beginning with s₀ = 2, r₀ = 0 we can generate successive solutions of s² – 3r² = 4 by the recurrence

Naturally the characteristic polynomial for the right hand matrix is simply the characteristic polynomial

of the 2nd-order recurrence (1), and that recurrence itself can be recovered by eliminating r from the two first-order equations.

Torsten Sillke noticed, based on numerical evidence, that if p > 3 is a prime divisor of s_n – 1 then apparently p is necessarily congruent to 1 or 17 (mod 24) if n is odd, and it is congruent to 1 or 13 (mod 24) if n is even. He asked if this is true in general and, if so, for a proof.

To prove that this conjecture is correct, let's re-write the basic Pellian equation in the form

which can be factored to give

By construction, s_n is divisible by exactly one power of 2 if n is even, and by two powers of 2 if n is odd. Now, if n is even, there is an odd integer y such that y = s/2, and we have

where the two factors on the left are coprime except for a single common factor of 2. Also, from congruence considerations we know that s/2 + 1 is not divisible by 3, so we have integers a,b such that

which implies that

Notice that these are special cases of the quadratic forms

where gcd(x,Ny) = 1. Euler (and probably Fermat) proved that, for the cases N = 1, ±2, 3, every prime divisor of this form is also expressible in this form, and the prime p can divide a number of this form if and only if (–N) is a square modulo p. Thus, any prime divisor of a number of the form a² – 3 (with a prime to 3) must be congruent to 1, 11, 13, or 23 modulo 24, because those are the only primes modulo which 3 is a square. Likewise, any prime divisor of a number of the form 1 + 3b² must be congruent to 1, 7, 13, or 19 modulo 24, because those are the prime modulo which -3 is a square. Now, since s(n) – 1 must be of both those forms if n is even, it's clear that any prime divisor must be in the intersection of those two sets of residues, so it can only be 1 or 13 (mod 24).

For the case of odd n there is an odd integer y such that 2y = s/2, and we have

The two factors on the left are coprime, so one must be a square and the other must be 3 times a square. It's easy to show that s_n/2 – 1 is not divisible by 3 if n is odd, so we have integers a,b such that

from which it follows that

So in this case, after factoring out the prime 3, we need only consider the prime divisors of numbers that have both the forms

with x coprime to 2y. It follows that any prime divisor of 2a² – 1 must be a prime p modulo which 2 is a square, so p must be congruent to 1, 7, 17, or 23 (mod 24). Also, any prime divisor of 2b² + 1 (other than 3) must be a prime p modulo which -2 is a square, so p must be congruent to 1, 3, 11, 17, or 19 (mod 24). Again, since s_n – 1 must be of both those forms if n is odd, it's clear that any prime divisor must be in the intersection of those two sets of residues, so it can only be 1 or 17 (mod 24) (once we have factored out the power of 3). This completes the proof of Sillke's conjecture.

Incidentally, without even invoking the theory of quadratic forms we can nearly prove the above result by simple congruence considerations. We know that s_n – 1 is congruent to 3 (mod 24) for all odd indices n, so it's obvious that the product of the remaining factors of (s_n – 1)/3 must be either 1 or 17. (We can rule out 9 because 2a² – 1 cannot be congruent to 9 modulo 24). Therefore, s_n – 1 = 3m where m = 1 or 17. If m is a prime, then we are done. If m is composite, the question is whether each of the prime factors of m is necessarily congruent to 1 or 17 (mod 24).

If we examine the multiplication table (mod 24) we find that if m = uv then the only possible values of the factors u and v are (mod 24)

and

Therefore, any prime factors of m must be in one of these residue classes. However, we can exclude many of these, recalling the fact that

This shows that if there exists an index j such that V(j) is congruent to 1 (mod p) then

which implies that -1 must be a square modulo p, which means that p = 1 (mod 4). Thus we can rule out p = 7, 11, 19, or 23 (mod 24), which just leaves the following possibilities for any 2-part factorizations of m (mod 24)

and

So, the only part of Sillke's conjecture (for odd n) that requires the theory of quadratic forms is the assertion that 5 and 13 are ruled out.

Sillke had also stated another conjecture, based on the observation that a prime p > 3 divides some integer sn – 1 if and only if the period of the recurrence of s_j (mod p) is a multiple of 6. This conjecture is not too difficult to prove. First, let's review a little what's known about the periods of s_j modulo primes. (We'll restrict the discussion to 2nd-order recurrences modulo primes; for a discussion of recurrence periods of general nth-order recurrences modulo primes and composites, see Section 2.7 of Symmetric Pseudoprimes.

We know the period of s_n mod p divides p+1 if 3 is not a quadratic residue mod p, and divides p – 1 otherwise. Thus, if we denote the period of s_n mod p by T_p, we have

Of course, the primes congruent to 5 or 7 (mod 12) are congruent to 5,7,17, or 19 (mod 24), and the primes congruent to 1 or 11 (mod 12) are congruent to 1,11,13, or 23 (mod 24).

Now, remember that the only primes that divide s_n – 1 are congruent to 1, 13, or 17 (mod 24). If p is congruent to 1 or 13 then it is of the form p = 12j + 1, and so

On the other hand, if p is congruent to 17 (mod 24) then it is of the form p = 12j + 5 and we have

This shows that if p divides some s_n – 1 then T_p must be a multiple of 6 if k = 1, i.e., if the recurrence corresponds to a primitive root (mod p).

Conversely if p is congruent to 7 or 11 (mod 12), it cannot divide any s_n – 1, and T_p cannot be divisible by 6, because in those cases the numerator of T_p is either 12j + 8 or 12j + 10, neither of which is divisible by 6 for any value of k.

In view of all this, it's clear why Sillke's conjecture is likely to apply to most primes. The only uncertainty is whether k might divide out the 6 from the numerator of some period. This is essentially the same phenomenon that allows pseudoprimes to occur, i.e., aliasing, so that a field with one characteristic "looks like" a field with another, because k > 1.

To illustrate, here's a list of the primes that are in the "right" congruence classes to be possible divisors of s[n]–1, along with their periods and the corresponding values of k. I'll put an asterisk (*) next to those that do not divide s_n – 1:

  p     T[p]     k           p      T[p]    k

 --     ----    ---         ---     ---    ---

 13      12      1          449     150      3

 17      18      1          457     228      2

 37      36      1          521 *    58      9

 41 *    14      3          541     540      1

 61      60      1          569     114      5

 73      36      2          577     288      2

 89      90      1          593     594      1

 97 *    16      6          601     300      2

109     108      1          613     204      3

113     114      1          617     618      1

137     138      1          641     642      1

157     156      1          661      60     11

181 *    20      9          673     336      2

193      24      8          709     708      1

229     228      1          733 *   244      3

233     234      1          757      84      9

241      30      8          761     762      1

257     258      1          769     192      4

277 *    92      3          809     810      1

281     282      1          829     276      3

313      78      4          853 *   284      3

337 *    56      6          857     858      1

349 *   116      3          877     876      1

353 *   118      3          881     294      3

373 *   124      3          929     930      1

397     396      1          937     234      4

401     402      1          953     954      1

409     204      2          977 *   326      3

421     420      1          997     996      1

433     216      2

As required, gcd(k,6) > 1 for all cases where T_p is not divisible by 6. In fact, all the non-divisors have k a multiple of 3. This might lead us to suspect the converse, i.e., that p cannot be a divisor if k is a multiple of 3, but that's is certainly not the case, as shown by the primes 449, 613, 757, 829, etc. On the other hand, we might suspect that p must be a divisor if k is not divisible by 3, and this is certainly true for all p < 1000. This really just expresses the fact that all the periods are even numbers, so divisibility by 3 automatically implies divisibility by 6.

By the way, notice that in most (2/3) of the cases, the numerator of T_p is automatically not only a multiple of 6, it is a multiple of 12, so it has a power of 2 to spare. Also, in 1/3 of the cases the numerator is a multiple of 24, so it has two powers of 2 to spare.

We're now in a position to prove Sillke's second conjecture, i.e., the observation that the period of the recurrence

modulo p is divisible by 6 if any only if p divides s_n – 1 for some integer n. The key identity is

for any integers n and k. (Notice that with n = 1 this is simply a re-statement of the basic recurrence, and it's easy to show by induction that it's true for all n.) Now, suppose a prime p divides s_n – 1 for some particular index n. In other words, we have s_n = 1 (mod p). It follows from (3) if we set k = n we have

(Of course, it also follows that s[4n], s[8n], etc., are all congruent to -1 (mod p).) We also know that s_k = s_-k for all k, so on the condition that there is an integer n such that s_n = 1 (mod p) we have

This provides more than enough values to infer the recurrence relation for the sequence in steps of n:

so we have the complete cycle

which repeats ad infinitum. The period of the recurrence (mod p) must be a multiple of this cycle, so it must be divisible by 6. So we've proven that if p divides some s_n – 1 then the period of the recurrence (mod p) must be divisible by 6.

What about the converse? If the period of the recurrence is a multiple of 6, must we necessarily find that s_n = 1 (mod p) for some index n? Yes, because if the period of the recurrence is 6m we know that s_6m = 2 (mod p), which by equation (4) implies that s_3m = +2 or -2 (mod p). We also have the relation

which implies that

Now, it's important to realize that we can rule out any value of the sequence being congruent to +2 (mod p) between s₀ and s_6m, because the sequence has a fundamental period j if and only if j is the least positive integer such that s_j = 2. This is due to the fact that the meta-sequence s_-j, s₀, s_j, s_2j,... has a period of 1, and therefore every sequence s_kj+r has period 1. (A full account of this is given in Section 2.5 of Symmetric Pseudoprimes. The key point is that the recurrence for the sequence s_kn is

and so if s_k = 2 (mod p) for any index k we have

which has the characteristic polynomial

In other words, it factors into the degenerate 1st-order recurrence s_kn = s_k(n–1), and since n can be any rational number such that kn is an integer, we can set n = m + r/k to give

which shows that the entire s sequence has period k.

Therefore, since the premise is that 6m is the fundamental period of the recurrence (mod p), we know that s_3m = -2, which implies that s_m = +1 or –2. However, if s_m = –2 then s_2m = +2, which is impossible, so we must have s_m = 1 (mod p), which proves that p divides s_m – 1. This concludes the proof of Sillke's 2nd conjecture.

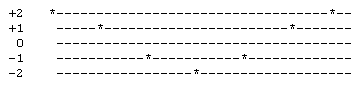
By the way, it's interesting to observe that if p divides some s_n – 1 then we have the meta sequence of values

Moreover, recall that most of the periods are actually divisible by 12, and some by 24, and in those cases we know that p divides s_u itself, which means that s_u = 0 (mod p) for some u. Indeed, we find that the 0's always occur mid-way between the +1 and –1, so we have

These are precisely the lattice values of 2cos(2πk/T) where T is the period of the recurrence modulo p. This function will give a value of 1 if and only if there is an integer k such that k/T = 1/6, which there will be iff the period T is a multiple of 6.

It isn't surprising that we have this relation, because notice that the recurrence of the meta-sequence S_k = s_nk given by equation (5) has the characteristic equation x² – x + 1, whose roots are the primitive cube roots of –1, i.e.,

and of course the values of the recurrence are simply

If we write r₁ and r₂ in exponential form we have

Recalling that the definition of the cosine function is cos(θ) = (e^iθ + e^–iθ)/2, we have the result S_k = 2 cos(kπ/6).

Return to MathPages Main Menu