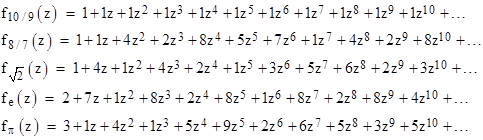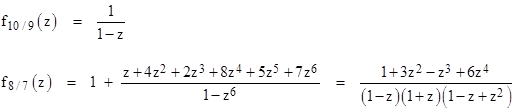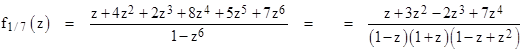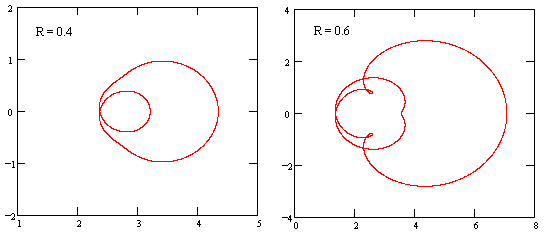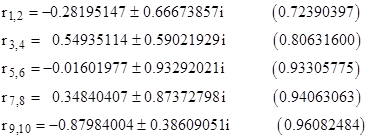Decimal Representations as Power Series

Decimal Representations as Power Series

For any given real number w let f_w(z) denote the power series whose coefficients are the decimal digits of w. A few examples of such functions are listed below.

Naturally we could define power series for representations in other bases besides 10, but a large number of decimal digits for various constants are readily available, so it’s convenient to focus on decimal representations. We should also note that the one-to-one correspondence is between power series and decimal representations, not real numbers, because some real numbers have more than one decimal representations. For example, we have the two alternative series f₁(z) = 1 and f₁(z) = 0 + 9z + 9z² + 9z³ + …

Each of the power series defined above has a radius of convergence of 1, since their values are always less than 9 times the geometric series. The first two functions, corresponding to the rational numbers 10/9 and 8/7 respectively, have the closed form expressions

Thus the function f_10/9(z) has no roots and just a single pole, whereas the function f_8/7(z) has four roots and four poles. These expressions represent the analytic continuations of the respective power series to the entire complex plane.

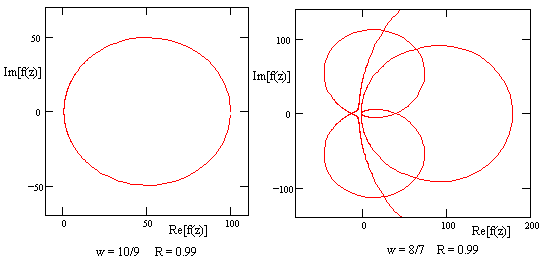
To assess the behavior of such power series within the radius of convergence, it’s convenient to plot the imaginary part versus the real part of f(Re^iθ) for a fixed value of R (less than 1) as θ ranges from 0 to 2π.

By varying R from 0 to 1, we can confirm that the function f_10/9 has no roots, whereas the function f_8/7 has the four roots

As expected, these values are the roots of the equation

which is the numerator of the generating function for f_8/7(z). Thus we have another way (in addition to the Taylor series expansion method) of determining the analytic continuation of a given power series: Find the roots of the function within the radius of convergence, and use these to construct the “numerator” of the generating function for the power series. Then knowledge of the poles enables us to determine the denominator of the generating function. Of course, for the decimal representations of rational numbers, this simply amounts to identifying the repeating string of digits and then converting to a finite polynomial using the geometric series. Thus, had we considered the function corresponding to the decimal representation of 1/7 instead of 8/7, we would have arrived at the generating function

which has the roots

Conversely, since these roots lie within the radius of convergence of the power series, we could determine these roots from the series and infer the generating function. However, this method is valid only if all the roots lie within the radius of convergence, which need not be the case, even for power series corresponding to the decimal representations of simple rational numbers. For example, consider the fraction

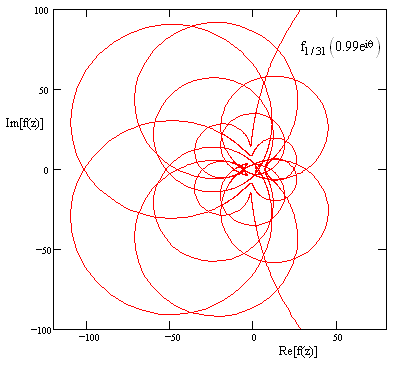
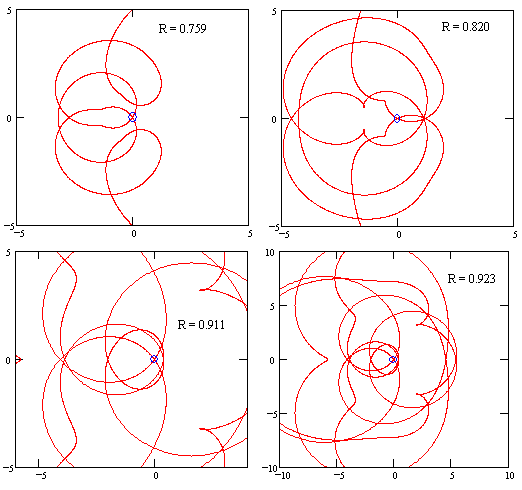
The non-zero roots of the polynomial 3z² + 2z³ + … + 9z¹⁵ consist of one real root of magnitude 1.148 and six complex conjugate pairs with magnitudes 0.759, 0.820, 0.911, 0.923, 1.005, and 1.022. Thus only 10 of the 15 roots could be determined simply by evaluating the power series directly. Nevertheless, it seems possible to recognize from the behavior of the power series inside its radius of convergence that it does indeed have a finite generating function. The figure below shows the imaginary part versus the real part of f_1/31(z) for z = 0.99e^iθ.

Although this appears somewhat chaotic, it still exhibits recognizable continuous arcs, even though this is for values of z quite close to the boundary of convergence. A well-behaved shape of this kind is characteristic of f_w(z) for rational values of w, even when some of the roots lie outside the radius of convergence. The loci for magnitudes corresponding to the four pairs of complex conjugate roots are shown below.

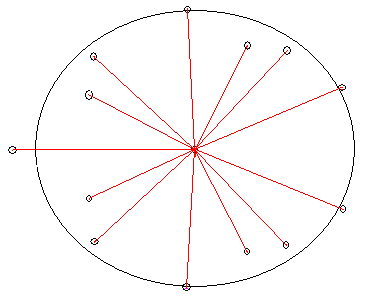
Naturally the locus passes through zero twice in each case, corresponding to the values ±θ of the complex conjugate roots. All fifteen of the roots of f_1/31(z) are shown in the figure below.

In view of how easily we can (in principle) analytically continue the decimal representations of rational numbers, one might think we could analytically continue the decimal representation of just about any real number. However, for irrational numbers this turns out to be impossible, because the boundary of the region of convergence of the power series for an irrational number is everywhere singular. This doesn’t imply that every point on the boundary is a pole. A function is also singular at branch points, and we will find that for the power series corresponding to the decimal representation of any irrational number every point on the unit circle is either a pole or a branch point.

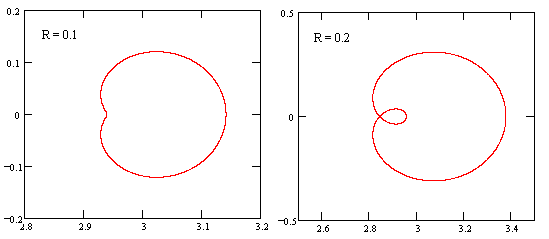
To illustrate, consider the power series f_π(z) corresponding to the decimal representation of the real number π = 3.14159… The loci of complex values of f_π(z) for |z| = R are shown below for R = 0.1 and R = 0.2.

Naturally as R goes to zero this locus approaches a circle of radius R centered on the constant coefficient 3. As R increases, the circle of arguments represented by |z| = R maps to a more complicated locus, and in particular the argument z = R maps to a real number whose value increases toward infinity as R approaches 1, since z = 1 is a pole of the function. The rest of the locus evolves as shown in the figures below for R = 0.4 and R = 0.6.

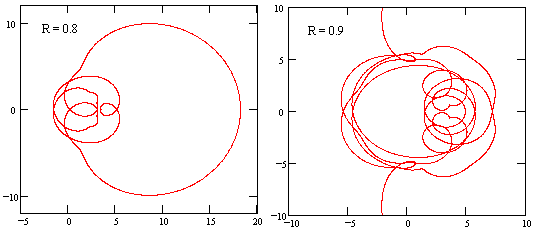
As can be seen especially in the plot for R = 0.6, the cusps become loops, and then more cusps develop in those loops, and so on. Obviously there are no roots with |z| in this range, since the loci do not encompass zero. However, by the time R has increased to 0.8 the locus encompasses zero, as shown in the left-hand figure below, so we know the function f_π(z) has a root in this range.

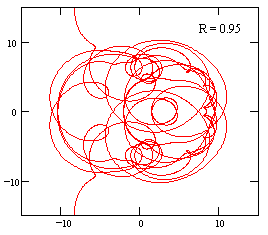
We also see, especially with R = 0.9, that the complexity of the locus continues to increase, and it circles the origin many times. This is even more apparent for the locus with R = 0.95 shown below.

The locus is already taking on a fractal characteristic, which continues to develop as R approaches 1. One way of looking at this is to attempt to analytically continue the function outside the unit circle by applying the Taylor series expansion. We find that, unlike the power series based on rational numbers, the region of convergence cannot be extended outside the unit circle for a power series based on any irrational number. It appears that the number of terms necessary for convergence of continued series outside the unit circle is related to the length of the repeating string of digits, and since this length is infinite for irrational numbers (i.e., the digits never fall into a repeating pattern) the series cannot be analytically extended.

We can, however, determine many roots of f_π(z) within its region of convergence. The first (i.e., smallest) several pairs of complex conjugate roots are listed below along with their magnitudes.

Presumably there are infinitely many roots, increasing in density as the magnitudes approach 1. We can expand the polynomial about other points within the region of convergence, but we invariably find that the radii of convergence of these new series extend only to the unit circle, so we are unable to analytically continue this function. We saw in the case of series corresponding to rational numbers that we could analytically continue the series based on the roots and poles, but since there are infinitely many roots (not to mention infinitely many singular points) for series based on irrational numbers, there doesn’t appear to be any way of expressing the function in terms of less information than simply specify each of the infinitely many digits. We could, of course, consider functions constructed from the roots and pole, such as

where k equals 3 divided by the product of the roots, but this doesn’t seem to provide a valid representation of f_π(z), even inside the region of convergence.

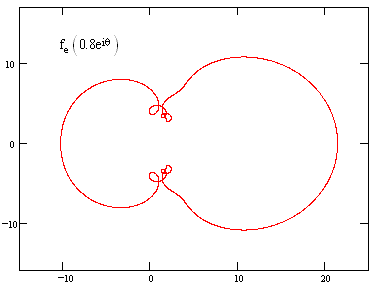
The power series corresponding to the decimal representation of each real number is unique. The figure below shows the complex locus for the power series f_e(z).

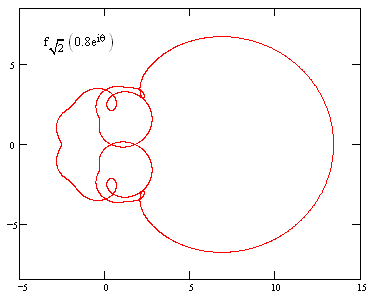
Lastly, the figure below shows a locus for the series based on the algebraic number that is the square root of 2.

It would be interesting to know what properties of a real number can be inferred from a locus of this kind based on the decimal representation of the number. It ought to be possible to infer the number from any finite segment of the locus.

Return to MathPages Main Menu