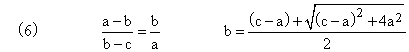|
The Ten Means of Ancient Greece |
|
|
|
The ancient Greeks defined a list of ten distinct "means", including most of the well-known means that we still use today. However, oddly enough, they never explicitly defined what we call the root-mean-square (although it can be constructed by composition of some of their means). In Pythagoras's time there were just three means, which we call the arithmetic, the geometric, and the harmonic (originally known as the "subcontrary mean"). Later, three more "means" were added, possibly by Eudoxus. These six are described in the article Iterated Means. The last four means were added by two later Pythagoreans, Myonides and Euphranor. We actually have a listing of "The Ten Means" from two different ancient authors (Nicomachus and Pappus), but the lists are not quite identical. They each give one "mean" that the other left out, so taking the two lists together, we have eleven distinct means in all. |
|
|
|
Consider three quantities a,b,c such that a > b > c, where we wish to make b the "mean" of a and c. Notice that we can form three positive differences with these quantities: (a-b), (b-c), and (a-c). The Greeks worked on the idea of equating a ratio of two of these differences to a ratio of two of the original quantities (not necessarily distinct). For example, if we set the ratio (a-b)/(b-c) equal to the ratio a/b, the result is b2 = ac, which represents the geometric mean. |
|
|
|
Of all the possible ways of doing this, several of them are automatically ruled out by the assumed inequalities on a,b,c. The ones that are not (necessarily) ruled out are the ten (actually eleven) means as summarized below: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Some of these are obviously not very intuitively useful definitions of "means". For example, using the 11th mean we would have m11(5,4) = 1. This mean presumably was included because it doesn't necessarily violate the assumed inequalities, e.g., m11(5,1) = 4, but it seems only marginally acceptable. On the other hand, it's interesting to note that m5(2,1) equals f, the golden proportion (1.618…). We might also note that the 2nd mean of the 3rd and 4th means on this list is equivalent to what we call the root-mean-square. |
|
|
|
Anyway, it's not too surprising that only the arithmetic, geometric, and harmonic have survived in common usage. This process of broad abstract definition followed by pragmatic selection reminds me of how Western music originally had seven distinctly identified "modes" (Ionian, Dorian, Phrygian, Lydian, Mixolydian, Aeolian, Locrian), and then over time we discarded all but two of them (the Ionian and Aeolian), which we call the "major" and natural "minor" scales. This is doubly fitting, considering that the original concept of numerical "means" among the Pythagoreans and others was closely involved with the study of musical tones and scales. |
|
|