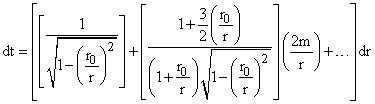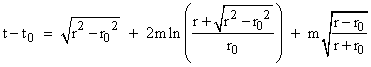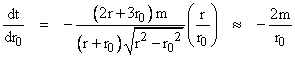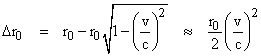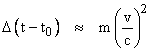Measuring the Speed of Gravity

According to the theory of relativity, no energy or information can propagate faster than the universal constant c, which is evidently the speed at which electromagnetic waves propagate in vacuum. Moreover, every physical phenomenon is (at least locally) covariant with respect to Lorentz transformations, in which the constant c appears. From the standpoint of the relativity theory as it was developed by Lorentz and others prior to 1905, this was interpreted as meaning that all the forces of nature, including not only electromagnetism but also gravity and whatever forces are responsible for holding atoms and sub-atomic particles together, contain the constant c in their formulations. Of course, this remarkable coincidence would be explainable if all forces could be shown to be fundamentally electromagnetic, but this was clearly not the case, because (among other reasons) electromagnetism by itself cannot account for stable configurations (Earnshaw’s theorem).

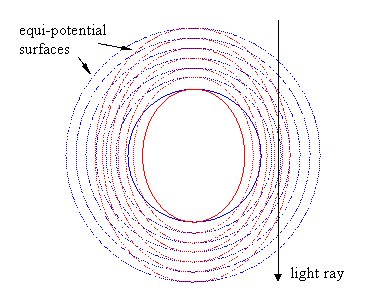
In the summer of 1905 Poincare wrote two papers on the postulate of relativity and the implications it has for a broad range of physical phenomena, especially gravitation. He pointed out that if the postulate of relativity is true in all generality, i.e., if there was really no way to establish an absolute state of motion, then the force of gravity must be Lorentz covariant, which implies that the universal constant c enters into the formulation of the true law of gravity. In effect, changes in the gravitational field cannot propagate faster than c, and assuming gravity is mediated in a massless way, it cannot propagate slower than c (all speeds being referred to inertial or quasi-inertial systems of coordinates.) It also follows that the spherical surfaces of constant gravitational potential surrounding a spherical mass at rest must transform into ellipsoids, flattened in the direction of motion, with respect to a relatively moving system of inertial coordinates. This is illustrated in the figure below.

Of course, the massive body itself also exhibits a spatial contraction of [1–(v/c)²]^1/2 in the direction of motion, attributable to the fact that the molecular forces maintaining the shape of the body are Lorentz-covariant as well. It’s important to recognize that the spatial contraction of the equi-potential surfaces is directly related to the fact that changes in the field propagate at the speed c. If a physical force whose changes propagated faster than c were ever found, the (Lorentzian) principle of relativity would obviously fail, the force would not be Lorentz-covariant, and the equi-potential surfaces corresponding to that force would not spatially contract in accord with special relativity.

In particular, the hypothesis of an instantaneous force implies a definite absolute simultaneity. In that case it would be possible to identify precisely one of the inertial frames of reference as the “true” absolute rest frame, and the laws of physics would depend on absolute speed. This was already realized in 1917 by James Jeans, who noted in a letter to Oliver Lodge that if the shape of the Sun were determined entirely by forces (such as electromagnetism) that propagate at the speed of light, then the equilibrium shape of the Sun moving with velocity v would be contracted into an ellipsoid by the Fitzgerald factor [1–(v/c)²]^1/2 in the direction of motion, whereas if we assume that (unlike electromagnetism) the force of gravity propagates instantaneously, the equilibrium shape of the Sun would not be Lorentz covariant. In this case "a compromise would be effected between electromagnetic forces, striving for a Fitzgerald ellipsoid, and the gravitational forces striving for a strictly spherical shape. The result would be an ellipsoid less flat than the Fitzgerald one. From this difference between the contraction of the Sun and his measuring rod, an observer could determine v".

If we hypothesize the existence of a force whose disturbances propagate with a speed c_f much greater than c but still finite, we would need to decide whether to regard c_f as the new limiting speed on which to base a new theory of relativity (either in place of, or in addition to, c) or to conclude that there was no finite upper bound on speeds and thereby arrive again at absolute simultaneity. The theoretical possibility of constructing a relativistic spacetime metric with more than one characteristic speed has been considered (see Higher Order Metrics), but the variety of possibilities is so great that it would be difficult to single out just one as the most likely candidate in case conventional relativity were to fail.

The question arises as to whether we can, by examining the gravitational fields of large massive bodies, confirm the Lorentz-contraction of the equi-potential surfaces, thereby confirming (indirectly) the presumption that gravitational disturbances propagate at the characteristic speed c. One approach would be by means of careful geodesy using electromagnetic signals to determine the shape of the Earth with enough precision to establish whether or not it is Lorentz-covariant. On the hypothesis that changes in gravity propagate much faster than light, we would expect the electromagnetic measurements to be Lorentz-contracted due to the absolute motion of the Earth, whereas the shape of the Earth (being governed primarily by the gravitational force) would not, and this ought to show up as an anisotropy in the shape of the Earth in the direction of the Earth’s absolute motion (as measured by electromagnetic signals).

Now, since Jupiter is moving (with respect to the Sun’s frame of reference) with a speed of about 0.0000437c, it’s equi-potential surfaces ought to be contracted (with respect to the Sun’s frame of reference) by a factor that differs from unity by about (9.53)10^–10. However, this is not the relevant speed, because the Sun and the entire solar system share a much greater velocity, about (3.7)10⁵ m/sec = 0.0012c, relative to the isotropic frame of the cosmic background radiation. We are accustomed to think that, since the Earth shares most of this motion, it should be irrelevant, but this is implicitly based on the assumption that gravity is Lorentz-covariant, which is precisely the proposition we are trying to test. If, as discussed above, we hypothesize that gravity is an instantaneous force (or at least many times faster than c), then it effectively establishes an absolute simultaneity and an absolute inertial rest frame. If we take as the absolute rest frame the isotropic rest frame of the cosmic background radiation (for lack of a more plausible alternative), we would expect to find that the surfaces of constant gravitational potential would not exhibit the same Fitzgerald contraction as do forces and fields that are Lorentz-covariant. Therefore, the hypothesis that gravitational disturbances propagate much faster than c (the constant that appears in the Lorentz transformation) implies that we ought to observe anisotropies in the shapes and gravitational fields of the Sun and planets (including the Earth) relative to our electromagnetic measuring conventions, which are Lorentz covariant. So, taking the full “absolute” speed of the solar system, the relevant contraction factor actually differs from unity by about (1.44)10^–6. We would need to look for an anisotropy of this magnitude in the apparent size of the Earth along an axis aligned with the solar system’s motion. It’s conceivable that we already have sufficiently accurate measurements from satellites to rule out any such effect.

Another possible approach would be to make use of the “Shapiro time delay” for rays of starlight passing near a large massive body such as the Sun or the planet Jupiter, as illustrated below. (Each of these bodies has a significant speed relative to what could be argued is the absolute rest frame if such a thing exists, which is basically what these observations are attempting to discover.)

If we neglect the effect of gravity, the time required for a pulse of light to go from its point of nearest approach at a radial distance r₀ from Jupiter’s center to a point on the Earth at a distance r from Jupiter’s center would be (to the first order) given by the null interval t – t₀ = (r² – r₀²)^1/2. However, assuming the Schwarzschild metric is valid at least for a “stationary” Jupiter of mass m, general relativity tells us (see the article Bending Light) that

Expanding the fraction on the right side in powers of the small quantity 2m/r gives

Integrating this from (t₀,r₀) to (t,r), we get the time required for a pulse of light to go from the point of nearest approach at r₀ to the arbitrary radial (Schwarzschild) distance r

The second two terms represent an additional time delay due to the gravitational field. Differentiating with respect to r₀, we get

The effective change in r₀ due to contraction of the potential field is

Thus the shift in the delay time due to this effect is

It might seem strange that this shift is independent of r₀ (to the lowest order of approximation), but it is understandable if we remember that Δr₀ is proportional to r₀, so although the shift per unit of change in r₀ becomes less, the change in r₀ becomes greater (for a given speed) as r₀ increases. For Jupiter, whose mass in geometric units is about 1.4 meters, the shift in the Shapiro time delay amounts to about (8.9)10^–18 seconds if we use just the orbital speed, and this effect is presumably too small to be measured. However, using the speed of the solar system, and considering the Sun, which has a mass of 1.4 km in geometric units, this leads to a shift in the Shapiro time delay of 0.002 meters, which is about (6.7)10^–12 seconds. This is admittedly very small, but by examining the periodic variations in light from a pulsar as the rays pass near the disk of the Sun, we could, in principle, determine how the gravitational potential varies as a function of the radial distance from the body. This would enable us to determine whether the equi-potential surfaces are contracted in the direction of motion consistent with Lorentz covariance.

Return to MathPages Main Menu