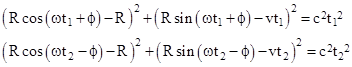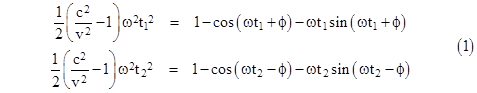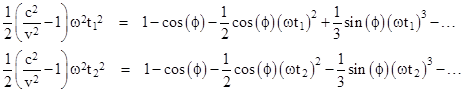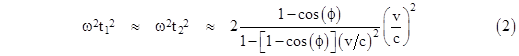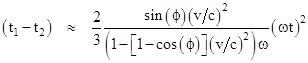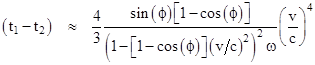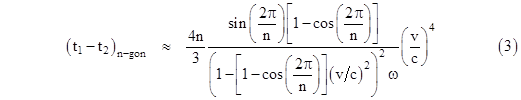Ballistic Sagnac

The Sagnac effect exhibited by two beams of light propagating in opposite directions around a rotating configuration of mirrors was described in a previous article. That analysis was based on the fact that a pulse of light propagates at the speed c with respect to any standard system of inertial coordinates, independent of the state of motion of the source. One of Sagnac’s motivations for examining this effect in 1913 was to test whether light really does possess this property – which he associated with wavelike propagation through a medium – or whether light propagates like Newtonian ballistic particles at a characteristic speed relative to the source. He reasoned that, under the ballistic assumption, there would be no phase shift, so the observed phase shift was presented as a disproof of the Newtonian ballistic conception of light.

By the way, when referring to the “Newtonian ballistic conception of light”, the word “Newtonian” is intended as a qualifier on the word “ballistic”, not on the phrase “conception of light”. It would be unfair and inaccurate to suggest that Newton regarded the principles of his mechanical ballistics to be a satisfactory basis for a conception of light. He often seemed to lean toward a corpuscular theory, but he recognized the difficulties of trying to account for all the phenomena of light if we regard the corpuscles as ordinary matter.

The assertion that Newtonian ballistic particles (in the context of Galilean spacetime) would exhibit no Sagnac effect is trivially true for a perfectly circular path, which might be conceived as the limit of infinitely many mirrors placed infinitesimally close together around the circumference of a rotating disk. In such a device, the emitter, receiver, and all the mirrors are moving at the speed v tangentially to the hub, and hence the particles are constantly moving (relative to the hub frame) at the speed c+v in the forward direction and c−v in the rearward direction. Also, the receiver is moving with the speed v away from each forward-going particle and toward each rearward-going particle, so the “closing speeds” are (c+v)−c and (c−v)+c respectively, both of which equal c. Each particle begins with the same separation from the receiver, and has the same closing speed, so the two particles will arrive simultaneously.

However, we can also consider a Sagnac device with a non-circular path. For example, suppose we have just three mirrors on a rotating platform, with perfectly elastic particles bouncing off these surfaces in both directions, as illustrated in the figure below.

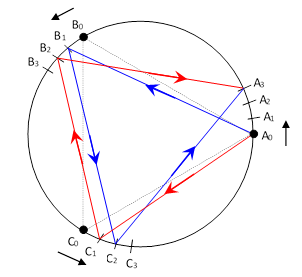
Initially the mirrors are at A₀, B₀, and C₀, and they are rotating about the center of the circle in the counter-clockwise direction. We can imagine two perfectly elastic particles emitted from A₀, one toward B and one toward C, at speeds such that they arrive after an amount of time Dt simultaneously at positions B₁ and C₁ respectively. They are reflected and proceed (in the same amount of time Dt) to the mirrors at the positions C₂ and B₂ respectively, where they are reflected again, and then both arrive simultaneously back at mirror A at the position A3. The paths are reversible, so the angles of incidence and reflection are equal. Also, since no work is done on the particles, the energy and hence the speeds of the particles remain constant. Thus with this arrangement there would be no Sagnac effect. However, the particles are obviously traversing different distances (with respect to the hub frame inertial coordinates), so in order for their arrivals to be simultaneous they must have different speeds (again, with respect to the hub frame). The question, then, is whether at the points of reflection the speeds of the particles are equal to each other relative to the rest frame of the local mirror.

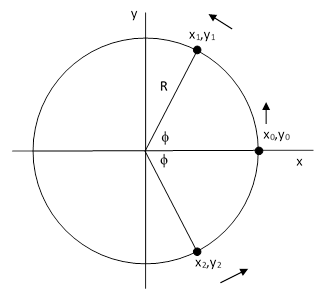
To determine this, consider the general polygonal case where consecutive mirrors are separated by an angle of ϕ, and are rotating around the circumference of a disk of radius R with angular speed ω and tangential speed v = ωR about the origin of Cartesian coordinates as shown below.

The coordinates of the leading and trailing mirrors are

We require that the speed of each particle must be a fixed number, which we will denote by c (not necessarily signifying the speed of light), relative to the rest frame of the emitter, which we take to be the mirror at x₀,y₀ in this case. To simplify the calculations, we first transform the coordinates of the leading and trailing mirrors to a system of inertial coordinates with origin at x₀,y₀ and moving in the positive y direction at the speed v, so that it represents the rest frame of the emitter. The required transformation is

Therefore the transformed coordinates of the leading and trailing mirrors are

The particles are emitted from the origin of the x′,y′ coordinates at time t = 0, and one moves at the speed c to the point x₁′,y₁′ at time t = t₁, whereas the other moves at speed c to the point x₂′,y₂′ at time t = t₂.  Thus we have

Inserting the previous expressions for x and y, we get

Expanding and simplifying, these can be written as

We could solve these equations for t₁ and t₂, and then subtract one from the other to give the difference between the travel times from one mirror to the next, but there is no simple closed-form solution of these equations. As an alternative, suppose the angle ωt through which the mirrors rotate during the transit of the particles from one to the next is quite small (i.e., the particles are moving much faster than the mirrors). In that case we can expand the right hand sides of these equations to give

The first three terms on the right hand sides of these equations are identical, so to this level of approximation the values of t₁ and t₂ are the same, and we can solve the equations up to this order to give

However, the equations differ in the third order (and all higher odd orders), so the values of t₁ and t₂ are no exactly equal (unless ϕ goes to 0 or π). This implies that, for general polygonal paths, there actually is a Sagnac effect for Newtonian ballistic particles, but it is of a much smaller order than the usual Sagnac effect for light. To determine the difference in transit times for the particles in the two directions, we can subtract one of the previous two expansions from the other, to give

Re-arranging terms, and letting t₁ + t₂ be approximated by 2t, and t₁³ + t₂³ by 2t³, where “t” is an estimate of both t₁ and t₂, we get

Substituting the approximation for (ωt)² from equation (2), this becomes

For a complete regular polygonal loop of n mirrors, we set ϕ = 2π/n and then multiply the entire expression by n to give the total difference in travel times for the two particles:

This shows that the lowest order “Sagnac effect” for ballistic particles moving at the speed c in opposite direction around a regular polygonal arrangement of mirrors moving with speed v is fourth order in v/c. If c is the speed of light and v is many orders of magnitude smaller (as in any realistic Sagnac device), this effect is so small as to be undetectable. On the other hand, since c need not denote the speed of light, we can impart a much smaller speed to the ballistic particles, so we could achieve any ratio v/c that we like. Of course, the convergence of our series expansion of (1) depends on the speeds being such that the mirrors move only a small angular distance in the time required for a particle to move from one mirror to the next. Also, our approximation assumes t₁ differs from t₂ by only a very small amount.

For any fixed values of v and c such that v/c is much smaller than 1, the squared quantity in the numerator is nearly equal to 1, and the overall effect is proportional to

To determine the angle that gives the maximum effect, we differentiate this quantity and set the result to zero, which gives

Multiplying through by 1 + cos(ϕ), and noting that 1 – cos(ϕ)² = sin(ϕ)², we can then divide through by sin(ϕ)² to give 1 + 2cos(ϕ) = 0, and hence cos(ϕ) = −1/2, from which it follows that ϕ = 2π/3. Therefore, as we would expect, the maximum effect occurs with three mirrors separated by 2π/3.

As an aside, attempts have sometimes been made to reconcile a Newtonian ballistic conception of light with the observed Sagnac effect. (Of course, to entertain any such conception of light, one must disregard all the experimental and observational evidence that the speed of light in terms of any standard inertial coordinate system is independent of the speed of the source.) One approach is to argue that reflections of light should be treated differently from emissions of light. Specifically, we might hypothesize that a particle of light always moves at the fixed speed c relative to the inertial rest frame coordinates of the original source at the moment of emission, even if the particle is reflected off one or more surfaces during its travel. Thus the hypothesis asserts that the speed of light is independent of the speed of any object that it encounters in a reflective interaction. Even aside from the ad hoc and incoherent nature of this hypothesis, it is obviously not consistent with Newtonian ballistic principles. It is actually an ether theory (which does indeed yield the observed Sagnac effect), except that instead of positing a single absolute ether, it assigns a separate ether for each emission event. Of course, if one adopted the electromagnetic world view, it could be argued that all electromagnetic energy is simply participating in reflective and scattering interactions, even when confined within material object, so we could never know what speed to expect, since we can’t know the state of motion of its original primal source, which supposedly governs its motion thereafter. One might argue that all light ultimately can be traced back to a single primal emission event, which would imply a single fixed ether theory. Ironically, the assumption that the speed of light is unaffected by scattering interactions is mutually exclusive with the “extinction” argument that was sometimes advanced by proponents of ballistic theories to discount astronomical observations (such as de Sitter’s) that show the speed of light is independent of the speed of the source.

Another odd variation on the Newtonian ballistic concept of light is based on the premises that (1) our empirical observations of light speed are all based on interference effects rather than direct timing of propagation, and (2) all interference phenomena have been fundamentally misinterpreted. Needless to say, the first premise (1) is false, because we have both astronomical and terrestrial observations of the actual arrival times for light emitted from objects moving at different speeds. Nevertheless, dedicated proponents of the ballistic concept are undaunted, and proceed to argue as if (1) was true, considering only interference-based observations. They argue, for example, that the time for two particles of light to move around a Sagnac device in opposite directions may be equal, and yet may still yield interference fringes in the receiver. (This is obviously inconsistent with very fundamental attributes of propagating electromagnetic waves, both in classical theory and in quantum electrodynamics, but, again, the proponents are undaunted.)  The idea is that each particle of light possesses its own “phase”, which advances in proportion to the optical path length that the particle has traversed. Typically this is taken to be length in terms of an absolute space, so it’s as if each particle of light contains an odometer, whose reading corresponds to the phase of the particle. When two or more particles collide, their effects are added together in accord with their phases. Thus if two particles hitting a receiver have opposite phases, they cancel out (destructive interference) and have no effect, whereas if they have the same phase their effects are added (constructive interference).

These peculiar hypotheses do indeed yield the observed Sagnac effect, because even though the two particles (moving in opposite directions around the loop) arrive simultaneously, they produce interference fringes due to the phase differences arising from the different optical path lengths relative to the posited absolute stationary space. However, this conception of light leads to many difficulties. First, it predicts a non-null result for the Michelson-Morley experiment, because the perpendicular rays of light traverse unequal distances relative to absolute space (assuming the Earth is moving relative to that space). This is ironic, because one of the original motivations for interest in ballistic theories was their ability to account for the Michelson-Morley experiment. By modifying the theory to force agreement with the Sagnac effect, we sacrifice agreement with Michelson-Morley. Second, it is at least debatable whether this modified ballistic theory is really a ballistic theory at all, because it relies on interaction between the light particles and the absolute fixed background to determine the phases of the particles. Thus it is really a hybrid, grafting a ballistic theory on top of a fixed ether theory. Third, we get two different kinds of frequency for a beam of light, one representing the number of particles per second, and another representing the rate of phase advance of each particle. In effect, if we consider a closely-spaced sequence of particles, the phase velocity is different from the particle velocity, so a given phase crest must move from one particle to another. Conversely, we can imagine an ordinary wave in the posited background space, and the only “ballistic” aspect is that we conceptually identify small segments of this wave as “particles”, which can be said to propagate at any speed we like, since the speed of these partitions has no effect – for a continuous beam of light. The only putative effect would be on the timing for the beginning and ending of a beam of light, e.g., the speed of the “leading edge” of a phase wave. But of course these timing effects (which are observed to be inconsistent with the ballistic hypothesis) are precisely what the Newtonian ballistic proponent declines to consider.

Oddly enough, the modern theory of electrodynamics and light, called quantum electrodynamics or QED, could with some plausibility be called a ballistic theory, since it satisfies the defining condition, i.e., light propagates at the speed c in terms of the standard inertial rest frame coordinates of the source. But it can also be called an ether theory, since it satisfies the defining condition, i.e., light propagates with a characteristic speed c (relative to a standard inertial coordinate system) independent of the motion of the source. Thus it isn’t surprising that the attempts to represent light in terms of Newtonian mechanical principles end up being hybrids, because this is unavoidable for a phenomenon that exhibits both particle and wave attributes.

It’s also interesting to note that Feynman’s “sum over paths” formulation of QED bears some resemblance to the Newtonian ballistic concept just described, i.e., we consider each possible path from emitter to receiver, and each path has an associated phase, proportional to the optical path length. The probability density is then the squared norm of the sum of all the complex amplitudes (representing the phases). However, there are fundamental differences between QED and the hypothesized Newtonian ballistic theory. For one, the phase of a photon does not advance during transit; instead, the light path simply represents a mapping from the emitter’s worldline to the receiver’s worldline, and the phase of the emitter is projected to the receiver. The phase depends on the path length only because a longer path conveys an earlier phase of the emitter. Second, in QED each photon interferes only with itself (if we neglect some higher-order non-linear effects), based on all the possible paths that it could follow. In contrast, the ballistic theory requires multiple particles to give interference. Thus they could not reproduce the results of Young’s two-slit experiment when performed with light of such low intensity that only a single particle/photon is registered at a time. QED correctly predicts the observed interference effects in such a case, whereas the ballistic theory must give no interference at all in this case. For the same reason, any classical ballistic theory is unable to give a satisfactory account for diffraction.

Return to MathPages Main Menu