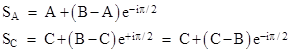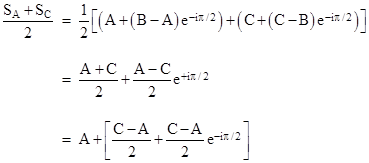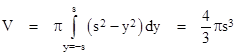Forests or Trees On A Complex Plain

Here's an interesting old problem: Pirates sail to a deserted island to bury their treasure, and they decide to place it in a spot that they can find later without using a map. They mark three trees A, B, and C, and then from B they pace off the distance to A, turn left 90 degrees and pace off the same distance, at which point they place a stake. Then they go back to B and pace off the distance to C, turn right 90 degrees and pace the same distance, and place another stake at this location. They bury the treasure mid-way between the two stakes, as illustrated in the figure below.

After burying the treasure, they remove the stakes and sail away. Unfortunately, when they return to dig up the treasure they discover that a storm has washes away the "B" tree. The problem is to locate the treasure.

We can imagine the trees on a complex plane, and represent the position of each tree by a complex number. Noting that multiplication of a complex number by e^iθ has the effect of rotating the position of that number about the origin through an angle θ in the counter-clockwise direction, the positions of the stakes can be written as

To get the second expression for S_C we multiplied by last term by 1 = −1/e^iπ. The treasure is buried at the mid-point of these two stakes, which is

Thus the location of the treasure is independent of the location of B. Starting at A, walk halfway to C, make a 90 degree right turn, and walk the same distance to the treasure.

Of course, there's also a "test-taker's solution" to this problem. If we assume the problem (with B washed away) has a unique answer, then it must give the same answer regardless of where B is located. Hence we can place B at any convenient point, such as the midpoint of the line connecting A and C, and locate the treasure. This gives the same answer as above, but it might not satisfy the traditional pirate's requirement for mathematical rigor, since it doesn’t include a proof that the answer is independent of the location of B.

One could create an entire sequence of problems like this, i.e., problems that have a trivial solution on the assumption that they actually have a (unique) solution. For example, we might encode the longitude and latitude of a treasure in the weight of golden sphere with a cylindrical hole of length L = 2s through its center. We're not given the radius R of the sphere, but if we were, the volume of this object could be computed by integrating the incremental annular slices at a height y relative to the center. These slices have an area given by π[(R² − y²) − r²)] where r is the radius of the cylindrical hole, so we can integrate this function from y = −s to +s. But of course r² = R² − s², so the parameter R drops out, and the volume integral is simply

The "test taker's solution of this problem is to reason that, since we haven't been given the radius of the sphere, the answer must be the same for any radius. In particular, if we take R = s then the cylindrical hole has zero diameter, and the volume of the entire sphere of radius s is simply (4/3)πs³.

Return to MathPages Main Menu