Bell Tests and Biased Samples

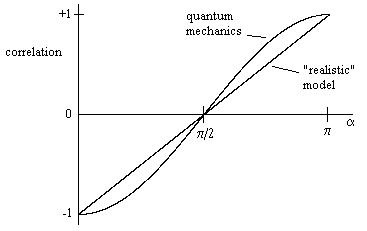
The natural first reaction after learning about Bell's inequalities for the results of separate quantum interactions is to try to think of a conventional realistic model that will reproduce the predictions of quantum mechanics and/or the results of actual experiments. The most common "realistic" model that comes to mind is one in which each particle is considered to possess a definite spin (or polarization) axis, and measurement along a given axis will return a positive or negative result corresponding to the sign of cos(θ) where θ is the difference between the spin axis and the chosen measurement axis. Assuming two "coupled" spin-1/2 particles in an EPR-type experiment have exactly opposite spin directions, this model agrees with the quantum mechanical predictions if the difference α between the two measurement angles is 0, π/2, or π (i.e. the measurement angles are equal, perpendicular, or opposite) with correlations are −1, 0, and +1, respectively. For intermediate values of α this “realistic” model predicts that the correlation varies linearly, thereby differing from the predictions of quantum mechanics as shown below

This simple “realistic” model is described in all elementary introductions to quantum mechanics, along with an explanation of why this model does not accurately represent what is observed. At this point the typical introductory text goes on to describe the effects of measurement inefficiency, noting that all EPR tests to date have relied on relatively low detection efficiencies, leaving open the theoretical possibility that the data is systematically biased in just such a way as to mimic the predictions of quantum mechanics.

If we wanted to persist in trying to construct a “realistic” model, we might try to modify the basic model so that it gives results approximating the predictions of quantum mechanics for all values of α by supposing that a measurement of a particle's spin has three possible outcomes: positive, negative, or null. The "null" outcome represents cases in which the measurement fails to resolve the spin of the particle. Further, we may suppose that a measurement is effective only if the positive or negative spin axis is within an arc subtended by a fixed angle β centered on the measurement axis. For example, the basic model assumed β equals π, from which it follows that a measurement is always effective. On the other hand, if β is some fixed value less than π, and if we neglect all particle-pairs in an EPR-type experiment when either of the spin measurements return "null", then the correlations of the remaining pairs can indeed approximate the correlations predicted by quantum mechanics.

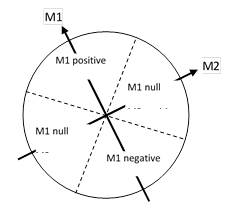
To illustrate, suppose β equals just π/2. This implies that each individual spin measurement is effective (i.e., returns a non-null result) over only half the range of possible spin axes. Now consider an EPR-type experiment in which we measure the spins of two coupled particles, with measurement axes that differ by α. Clearly if α equals π/2 (meaning the measurement axes are perpendicular) the effective ranges of the two measurements are mutually exclusive, so we will be unable to gather any correlation data at all. This situation is illustrated in the figure below.

However, for any other value of α the "effective quadrants" for measurements 1 and 2 will overlap. Also, notice that if α is less than π/2 the overlap will consist entirely of disagreements, whereas if α is greater than π/2 the overlap will consist entirely of agreements. Thus, assuming β = π/2, the correlation is -1 for α less than π/2, and +1 for alpha greater than π/2. The pair-measurement effectiveness is -1 at α = π/2 and ramps up to zero at α = 0 and α = π.

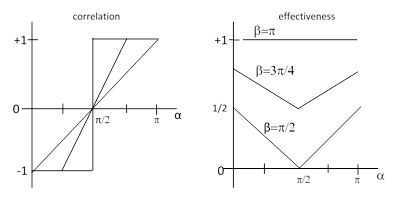
On the other hand, if we expand our assumed effectiveness arcs to β = 3π/4 we will record only disagreements when α is less than π/4, and only agreements when α is greater than 3π/4, and the correlation will vary linearly in between (because now we can get some overlap "on both sides" of the spin). Plots of the correlation and the pair-measurement effectiveness for β = π, 3π/4, and π/2 are shown below.

The correlations based on an assumption of β = 3π/4 clearly resemble the cosine curve predicted by quantum mechanics, and if we arbitrarily refine our "effectiveness" model so that the chances of a "null" result vary smoothly with α we can certainly tailor the correlation curve to agree exactly with the quantum mechanics predictions. All of this is quite familiar to anyone who has ever thought about tests of Bell's inequalities. It's understood that if our measurement efficiencies are low and there is a systematic effect such that the recorded pairs are a biased sample, then the simple Bell inequalities are no longer relevant. Furthermore, it's obvious that we can imagine realistic mechanisms that yield biases such that the simple quantum mechanics correlations are reproduced within the biased sample. The question is whether the hypothesis of such a bias is consistent with our observations. It’s worth noting that if our measurements were affected by the type of bias described above we would expect to see the measurement efficiency reach a minimum at α = π/2, but no such minimum appears in the data. (Aspect reported that although he found slight variations in his measurement efficiencies versus α, the variations were not significant.)

Now, if we were really desperate, we might try to explain the absence of a minimum in the efficiency at α = π/2 by assuming that the value of β is π for one of the measurements but something less than π for the other, in which case our measurement efficiency would be constant. But this shows that in order to match a particular set of quantum mechanical results we not only need to invoke a systematic bias in the measurement efficiencies, we need an asymmetric systematic bias, i.e., a bias that works on only one of the two particles in each coupled pair. Thus, we must imagine that when two particles emerge from a singlet state in opposite directions and interact with spin-measuring devices, one of them exhibits a definite spin when measured at any angle, but the other sometimes doesn't exhibit spin, if the measurement angle happens to be nearly perpendicular to its spin axis. Admittedly most actual experiments have involved physically asymmetric emissions, but we would require not just any asymmetry, but a very specific asymmetry, i.e., absolute perfection on one arm of the experiment and just the right amount of imperfection on the other arm to match the predictions of quantum mechanics. This kind of ad hoc maneuvering strikes most people as highly implausible and even unscientific.

By the way, in some experimental setups the null results would not go undetected, unless we believe that some of the particles with spins sufficiently near the UP/DOWN boundary simply disappear. For example, in a Stern-Gerlach apparatus if some of the particles (e.g., atoms of silver) exhibited no spin UP or DOWN, they would simply arrive at the center of the screen, having been deflected neither up nor down. But in fact when we perform such experiments (which have been done many times since the 1930's) we find that all the particles are deflected either UP or DOWN. Tests of the Bell inequalities have indeed been performed with massive ions, yielding essentially 100% detection, and the predictions of quantum mechanics were still upheld. However, the measurement events were so closely located in these experiments that one could still argue there was some sub-luminal communication. This possibility is called the locality loophole, which has been ruled out in some long-distance experiments with photons, although those experiments had low detection efficiency.

Thus some experiments have ruled out the detection loophole but not the locality loophole, and other experiments have ruled out the locality loophole but not the detection loophole. Most people would conclude that, since each loophole has been ruled out as the explanation for the apparent violation of Bell’s inequalities, we can say that all the loopholes have been closed. However, some have argued that different local realistic mechanisms might be at work in different experiments, thereby explaining the apparent violation of Bell’s inequalities. In other words, they suggest that in any experiment that has high enough detection efficiency to rule out the detection loophole, the measurement events is necessarily so close that we cannot rule out the locality loophole, and conversely, in any experiment that is carried out over sufficiently long distances to rule out the locality loophole we cannot achieve high enough detection efficiency to rule out the detection loophole. This sounds rather like the wave-particle duality of quantum mechanics, and indeed it’s even been suggested that quantum mechanics itself might preclude a loophole free test of Bell’s inequalities.

Despite the intriguing sound of this argument, experiments have been designed which would, at least in principle, close both the detection and the locality loophole simultaneously, although they have never been performed, and some would argue these designs would be impossible to carry out in practice. If there were enough incentive, they would probably be attempted, but most scientists are satisfied the matter has been adequately settled. Furthermore, the very objective is somewhat questionable, because one can always conceive of even more loopholes, some of which can never be closed, even in principle. For example, the common cause loophole can never be closed, because it’s always possible (especially in a deterministic context) for the choice of measurements to have some dependency on events in their common pasts.

Moreover, the proposition that no loophole-free test of Bell’s inequalities can ever be performed is actually much too narrow. No loophole free test of anything can ever be performed. It is always possible to conceive of alternative explanations for the (apparent) outcome of any single experiment or observation. For example, the famous experiment of Michelson and Morley is consistent with an emission theory of light, and also with a fully dragged ether theory. But those theories are inconsistent with other experiments and observations. In general, only a combination of experiments is sufficient to constrain the degrees of freedom and make one particular theory the most plausible. But if we exclude combinations, and insist that no alternative theory has been ruled out unless all alternative theories are ruled out simultaneously by a single experiment or observation, then science itself becomes impossible. And of course, no single all-embracing super-experiment is even possible, because it is always be possible to conceive of additional loopholes by proposing various alternative hypotheses, if we have no standards of plausibility.

This has always been clear to thoughtful scientists. For example, Isaac Newton’s “Rules of Reasoning” stressed the fact that science relies on proposition inferred by general induction from experiments, “notwithstanding any contrary hypotheses that may be imagined”, and he noted that “this rule we must follow, that the argument of induction may not be evaded by hypotheses”.

Return to MathPages Main Menu