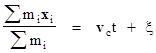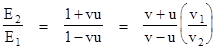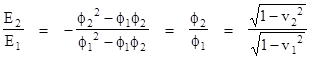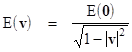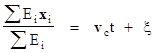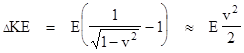Newtonian and Relativistic Conservation Laws

In Newtonian physics each individual body possessed a scalar mass m and a vector velocity v, resulting in a vector quantity of momentum p = mv. In this context, the total momentum and the total mass of an isolated system of bodies are conserved. This allows for the possibility that bodies may split or merge, and may exert forces on each other and mutually influence each others' motions. Thus we do not require that the states of motion of individual bodies be fixed, nor even that the number of bodies be fixed. Furthermore, we do not require, apriori, that the individual masses of the bodies be fixed, although this turns out to be a consequence of the conservation laws, as explained below.

A third conservation law emerged in Newtonian physics, namely, the conservation of a scalar E = m|v|²/2 called energy. It took longer for this law to be recognized, because energy can take different forms. For example, in a head-on collision of totally inelastic macroscopic bodies with equal speeds, it appears that the total mass and momentum are conserved, whereas it appears the total energy is not conserved, in the sense that the sum of the squared magnitudes of the bodies prior to the collision was positive whereas the sum of the squared magnitude of the combined body after the collision is zero. (It's interesting to compare this with the superposition or interference of two waves that are π radians out of phase with each other, so the combined wave has amplitude zero, even though the constituent waves have positive amplitudes.) The recognition of energy as a conserved quantity came along with the recognition that macroscopic bodies consist of bound configurations of smaller bodies, and if we consider the energy of a body as the sum of the energies of these constituent bodies, it becomes apparent that the total energy is conserved, even in the collision of inelastic bodies. In such collisions, the energy of the incoming macroscopic bodies is translated into increased internal motions of the constituent particles. On a macroscopic level this is manifested by an increase in the temperatures of the bodies. (We are leaving aside, for the moment, the dissipation of internal energy in the form of massless radiation.)

The principle of energy conservation implies some interesting consequences for the fundamental structure of mass. For example, if we hypothesize the existence of fundamental discrete particles of mass, with no constituent sub-particles or "degrees of freedom" that can be excited in the form of "temperature", then the collision of two such objects would necessarily be perfectly elastic. Conversely, if we observe an inelastic collision of two such fundamental objects (with no emission of energy), we would be compelled to conclude that the internal energies of the objects had somehow increased, i.e., that the energy is still present in some form. Thus we would have to believe that even these supposedly fundamental particles have some internal degrees of freedom (i.e., separate "parts") that can be excited. (Another possible outcome would be for two particles to meet and enter into a combined bound state with each other - like an electron in some orbit around a proton - so that the combination has a degree of freedom to absorb energy).

On the microscopic level, then, the Newtonian conservation laws for an isolated system of massive particles can be summarized as

where M and E are fixed scalars and P is a fixed vector. Intuitively, the conservation of momentum can also be expressed by saying that the center of mass of any isolated system of particles moves at constant speed in a straight line (with respect to any system of inertial coordinates). In other words, our intuitive notions suggest that the conservation of momentum can be expressed by the condition

where v_c and ξ are fixed. Multiplying through by M and differentiating with respect to t, this gives

The right hand side and the first term on the left hand both equal the momentum vector P, so this implies that the second term on the left hand side must vanish, i.e.,

Obviously a sufficient condition for this to be true is that the m_i values are individually constants. In fact, the condition remains satisfied even if we allow the transference of mass from one particle to another, provided the particles are coincident when the transference occurs. We can also allow the splitting of a particle into two or more particles of equal total mass, or the merging of two or more particles into a single particle of equal total mass. In general the above condition is satisfied if any changes in the individual m_i values occur in clusters of coincident particles (i.e., particles with the same x_i), with the total mass of such a configuration being constant, so that those x_i terms in the center-of-mass equation can be grouped together with a constant coefficient prior to differentiating.

Regarding the necessity of this restriction, notice that for an isolated system of just two particles the necessity follows immediately from the conservation laws, so we know that two isolated particles can transfer mass from one to the other only when they are in contact with each other. However, for a system of three or more particles this conclusion no long strictly applies, because we could hypothesize trinary interactions (for example) involving mass transfer between three separated particles. To illustrate, suppose we have three identical particles on the x axis at rest with respect to the x,t inertial coordinate system at the locations x₁ = 1, x₂ = 2, and x₃ = 4. Assume each particle has mass m, so the total mass is 3m, and the total momentum and energy is 0. At any instant, it is possible for the mass derivatives dm_i/dt to jump to the values 2, –3, and 1, or to any other combination of values that satisfy the two conditions

The total momentum and energy remain conserved, the total mass is identically constant, and the center of mass is unchanged, as long as the three mass derivatives satisfy these two equations - even though a trinary interaction at a distance is occurring. In the three-dimensional space of the mass derivatives, each of the above conditions represents a plane locus, and the intersection is a straight line, so the mass derivatives satisfying both conditions can be parameterized as (2k, –3k, k) for any value of k. In general, the space of allowable mass derivatives for N separate particles is of dimension N–2.

From this perspective, we see that Newtonian mechanics imposes an additional assumption, namely, that all mass interactions are fundamentally binary, i.e., that all mass interactions between any number of particles are just superpositions of simple binary interactions. Then, since binary interactions can only occur between coincident particles, we arrive at the contiguity of mass in Newtonian physics. This means that changes in the mass of any individual body can only occur contiguously with offsetting changes in the masses of other bodies at the same time and place, i.e., bodies in mutual contact with each other. The essential content of this contiguity requirement is that mass cannot be transferred from one body to another at a distance. Mass - in the Newtonian context - can be conveyed from one time and place to another only in the form of a massive body moving with some definite real speed. For this reason, mass is usually regarded as the fundamental ontological entity in Newtonian physics, moving along definite continuous paths through space and time.

Notice, however, that no such restriction is placed on momentum, i.e., it is not forbidden (in Newtonian physics) for momentum to be transferred at a distance. Indeed the Newtonian force of gravity was considered to be an agent of such "action at a distance", whereby separate bodies could exert mutual influence on each other, and mutually change their states of motion without being in direct contact with each other.

As mentioned above, the principle of energy conservation has often been obscured by the variety of forms that energy can take. In our discussion of inelastic collisions we noted that the temperatures of the bodies would rise, but we didn't mention the tendency for the temperature to subsequently drop, even if no mass particles are leaving the system. This would represent a violation of the energy principle if we did not introduce a new form of energy carried by massless entities, i.e., radiation. The energy of such radiation can't be expressed by a quantity of the form m|v|²/2 for any finite velocity v, because we are stipulating the m = 0 for radiation, so it isn't immediately clear how to incorporate massless energy into Newtonian physics. It also raises the question of whether the energy of a system could be re-distributed while the distribution of mass and momentum remain unchanged. Intuitively we would think not, i.e., it seems that all energy must have momentum, so this leads us to suspect that there is some larger symmetry underlying the separate conservations of mass and energy.

From the kinematics of special relativity it follows that the composition of two co-linear speeds u and v is (u+v)/(1+uv), and this in turn implies that energy carries momentum. This can be shown by considering two identical particles, each of mass-energy E, at rest at the origin of inertial coordinates (x,t). At time t = 0 these objects exert a mutual repulsive impulse on each other, and recoil in opposite directions at the speed u, one in the positive x direction and one in the negative x direction. Since the two particles are an isolated system, the center of mass-energy remains fixed at the origin.

Now consider the same situation with respect to an inertial coordinate system (x',t') whose spatial origin is moving in the negative x direction with speed v. Thus the center of mass-energy lies along the locus x' = vt'. By the speed composition formula, the two particles have speeds v₁ = (v–u)/(1–vu) and v₂ = (v+u)/(1+vu) respectively, so if we let E₁ and E₂ denote the mass-energy content of the two particles with respect to this frame of reference we have

Dividing through by E₁ and solving for the ratio E₂/E₁ gives

Solving the speed composition equations for v and u in terms of v₁ and v₂, we have

where ϕ₁ = (1–v₁²)^1/2 and ϕ₂ = (1–v₂²)^1/2. The values of v+u and v–u are

Inserting these expressions into the preceding equation gives

Consequently we have

This holds true for any values of u and v. In particular, if we set v = u, then v₁ = 0 and the left hand quantity is simply the rest mass-energy E of the particle. This shows that, in general, the mass-energy E(v) of a particle with velocity v is related to the mass-energy E(0) of the same particle at rest by

This quantity corresponds roughly to mass in Newtonian physics, and E(0) is sometimes called the rest mass. In the context of special relativity, mass-energy (rather than just mass) plays the role of the fundamental ontological entity. The center of mass-energy of an isolated system of objects moves at constant speed in a straight line with respect to any system of inertial coordinates. In place of the laws of conservation of mass and the conservation of energy, we have the single law of conservation of mass-energy. We also have conservation of momentum, provided momentum is now defined as the product vE of velocity and mass-energy. Hence we have

where E_tot and P are both fixed. Now, whereas Newtonian physics assumes the center of mass moves uniformly in a straight line, relativistic physics asserts that the center of mass-energy moves uniformly in a straight line (with respect to any system of inertial coordinates). In other words, we have

As in the Newtonian mass analogy, we can multiply through by the constant denominator and then differentiate (without assuming apriori that the "weighting coefficients" E_i are individually constant) to give

The first term on the left hand side is the momentum P, and the right hand side is the momentum of the same total amount of mass energy all moving with the velocity of the center of mass-energy, so it too equals P. Hence the second term on the left hand side must vanish, so we have

Also, differentiating the energy conservation condition gives

This shows that in relativistic physics the transference of mass-energy is subject to formally identical conditions as are imposed on the transference of mass in Newtonian physics. Again we find that, if we consider an isolated system of just two particles, these last two equations imply that the individual values of E₁ and E₂ cannot change except when the two particles coincide, i.e., when x₁ = x₂. If we assume that the presence of a third particle has no effect on the interactions of the first two particles, then in general it follows that mass-energy (and therefore momentum) is contiguous, just as mass is contiguous in Newtonian physics. But since mass-energy entails not only changes in the "matter content" but also changes in the state of motion of the particles, we see that this completely rules out any "action at a distance", purely as a consequence of the relativistic conservation laws - combined with the assumption of pairwise independence.

Of course, as in the case of Newtonian mass, we could imagine the possibility of higher-order interactions (e.g., trinary interactions), in which transference at a distance would not be immediately ruled out on the basis of the conservation laws with respect to any single inertial reference frame. However, in relativistic physics a greater restriction is imposed by the requirement that the conservation laws hold good with respect to every system of inertial coordinates, because the loci of simultaneity are not invariant under Lorentz transformations (unlike Galilean transformations, which do preserve simultaneity). This, combined with the conservation laws, automatically rules out "instantaneous" action at a distance in relativistic physics, because there are no absolute "instants". If a transfer of mass, energy, and/or momentum took place between two separate entities (with no mediating entity travelling from one to the other), the emission and absorption events would be simultaneous with respect to at most one inertial coordinate system, and not simultaneous with respect to all the others. It follows that the conservation laws would be violated during the interval between the emission and absorption.

It's clear that the quantities of mass, momentum, velocity, and energy are more closely inter-related in the context of special relativity than they are in Newtonian mechanics. This not only unifies the previously separate conservation laws for mass and energy, it also provides a very natural means of accounting for massless radiation. Recall that the total mass-energy E(v) of a body with rest mass-energy E(0) is given by

This presents the possibility of an object with zero rest mass-energy but non-zero total mass-energy, provided |v| = 1. In other words, massless radiation is possible, but only if it is propagated at the characteristic speed of the spacetime manifold, i.e., the speed of light. Since a speed of 1 transforms into a speed of 1 under any Lorentz transformation, this property is conserved with respect to all systems of inertial coordinates. If E_e is the total mass-energy of such an object with respect to the inertial rest coordinates of the emitter, then formally the quantity E(0) in the above equation must be expressible as E(0) = E_e (1 – |v|²)^1/2 in order to cancel the singularity at |v| = 1. The scalar E is positive and finite, so we can transform this to another inertial coordinate system whose spatial origin is moving at some speed and in some direction with respect to the emitter's rest frame. In fact, by the direction application of the formulas we used previously for the emission of two particles in opposite direction along the x axis, we can treat the case of massless particles by setting u = –v₁ = v₂ = 1. Recall that the speed -v is the speed (relative to the rest frame of the emitter) of the coordinate system in terms of which the energy is to be evaluated. We immediately have

By symmetry this implies that E₁ and E₂ both differ from the emitter-frame energy E_e by a factor equal to the square root of this quantity, so we have

These equations give the shift in energy evaluated with respect to a system moving in the opposite direction or in the same direction (respectively) as the radiation. In general, if the evaluation system is moving with a velocity v making an angle θ to the direction of the radiation (where θ is evaluated with respect to the emitter's rest frame), then

Historically, this was the starting point for Einstein's first derivation of mass-energy equivalence in his 1905 paper on the inertia of energy. He imagined a massive particle at rest with respect to one system of inertial coordinates x,y,z,t, emitting pulses of radiation of equal energy E/2 in opposite directions at the angles θ and π + θ relative to the x axis. The emitter remains at rest, but its energy content has been reduced by E. Then he evaluated the same situation with respect to a system of inertial coordinates x',y',z',t' whose spatial origin is moving with speed v in the positive x direction. Since cos(π+θ) = –cos(θ), we see that with respect to this frame of reference the energy of the two emitted bursts of radiation is

So, prior to the emissions, the emitting body had a certain amount of total energy, consisting of its internal energy U and its kinetic energy KE ≈ mv²/2. Subsequent to the emissions its total energy has presumably been reduced by the amount shown above. Some of this has come from the internal energy, which by definition is intrinsic and independent of the state of motion. The emitting body has lost an amount of energy equal to E relative to its rest frame, so we interpret this as the reduction in internal energy. With respect to the moving coordinates the emitting body has lost a slightly larger amount of energy, as shown above. The difference between these two can therefore be interpreted as the reduction in kinetic energy with respect to the moving system. This quantity is

Since the kinetic energy (at low speeds) is roughly mv²/2, and since the velocity v of the emitting body does not change as a result of the emissions, Einstein suggested that we should consider the inertial mass m to have been reduced by an amount E to account for this reduction in the kinetic energy. Thus the radiated energy E has carried away an equal amount of inertial mass, so we have E = m (or, in conventional units, E = mc²).

This "derivation" can be criticized for relying on some questionable assumptions, such as the idea that the internal energy is the same with respect to both systems of coordinates. Also, the approximate equalities appearing in this derivation are slightly distracting, especially to modern readers who are familiar with exact formulations. Einstein subsequently developed several other derivationss, always striving for maximum generality, trying to show that all forms of energy (not just electromagnetic radiation) carry inertia. Max Planck also developed improved derivations. Nevertheless, Einstein's first "derivation" (perhaps it should be called a consistency demonstration) has an undeniable charm, very illustrative of his distinctive early style, blending kinematics, thermodynamics, and electromagnetism.

Return to MathPages Main Menu