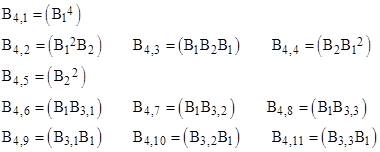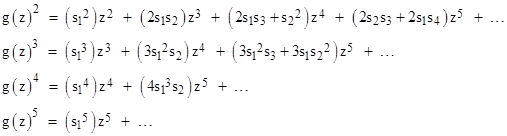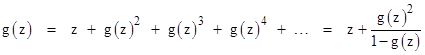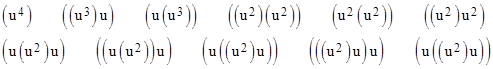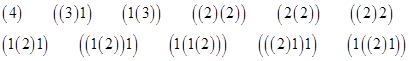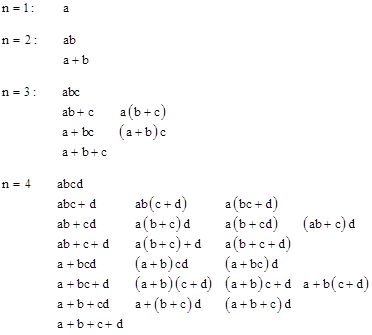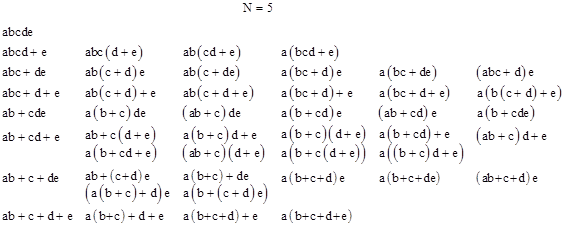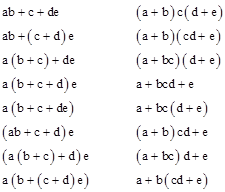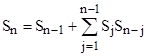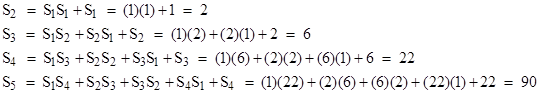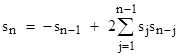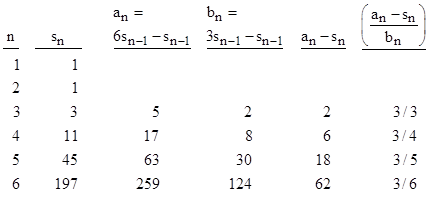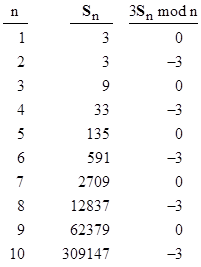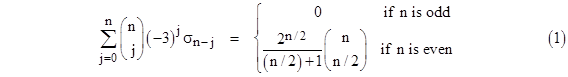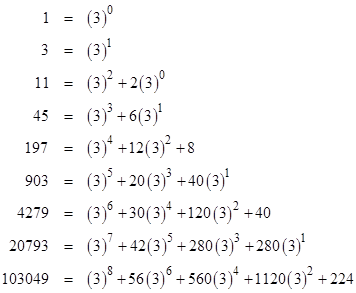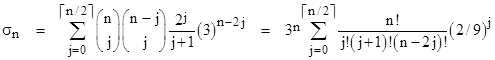Hipparchus on Compound Statements

As many figures dancing doth propose

As waves roll on the sea when tempests toss.

                                    Phrynichus

Hipparchus (190-127 BC) was the pre-eminent astronomer of the ancient world. Among his achievements was the discovery of the precession of the equinox, based on the recorded observations from earlier times. In addition to his astronomical work, he was also a mathematician who considered a variety of purely mathematical problems. According to Heath's "History of Greek Mathematics"

In pure mathematics [Hipparchus] is said to have considered a problem in permutations and combinations, the problem of finding the number of different possible combinations of 10 axioms or assumptions, which he made to be 103,049 (v.l. 101,049) or 310,952 according as the axioms were affirmed or denied. It seems impossible to make anything of these figures.

That last sentence expresses the frustration of scholars who have tried to understand exactly what Hipparchus was enumerating. (The parenthetical number in Heath’s comment will be explained below.) The only known source of information on these statements come from the Roman biographer Plutarch (50-120 AD), who referred to these enumerations twice in his writings. In an essay on the interesting subject of "whether there can be new diseases, and how [they are] caused", Plutarch discusses what would today be regarded as the combinatorial aspects of genetic mutations, and the likelihood of such mutations resulting in new diseases. In the course of this remarkably modern sounding discussion, he remarks that

Chrysippus says that the number of compound propositions that can be made from only ten simple propositions exceeds a million. (Hipparchus, to be sure, refuted this by showing that on the affirmative side there are 101,049 compound statements, and on the negative side 310,952.)

In another essay, entitled "Contradictions of the Stoics", Plutarch mentioned the same thing, this time using it to illustrate the carelessness of Chrysippus as a thinker (because, among other obvious "errors", Chrysippus had the audacity to dispute Plato's claim that humans absorb liquid nourishment through the lungs). However, in this passage the "affirmative" value quoted by Plutarch is different, thus accounting for the two versions of the number in Heath's account. Also, the statement of what is being enumerated is slightly different.

Chrysippus says, that the connections made by ten axioms amount to above a million in number, having neither searched diligently into it by himself nor attained to the truth by men experienced in it. All the arithmeticians refute Chrysippus, amongst whom is Hipparchus, demonstrating that the error of his computation is very great; since the affirmative makes of the ten axioms one hundred and three thousand forty and nine connections, and the negative three hundred and ten thousand nine hundred fifty and two.

Here we see that the things being enumerated are called "connections" rather than "compound propositions", and the number of affirmative connections is quoted as 103049 instead of the previously quoted value of 101049. The consensus of scholars seems to be that 103049 is more likely to have been the value given by Hipparchus, although this is necessarily uncertain. In any case, it so happens that 103049 is the number of "bracketings" of a string of 10 entities, as shown by the logician Ernst Schröder in 1870. (This coincidence was first noted by David Hough in 1994 while reading Richard Stanley’s book on combinatorics.) According to Schröder’s definition, a bracketing of one entity can be denoted as (x), and then all other bracketings are formed by taking the ordered products of bracketings and surrounding that product with brackets. There is only a single bracketing of two entities, given by forming the product of two (x) bracketings and surrounding them with brackets, resulting in ((x)(x)). Similarly we can form bracketings of three entities in three different ways, namely

Notice that the second and third of these are considered distinct, even though they consist of the product of the same two bracketings, because they occur in a different order. If we let B₁ denote (x) and B₂ denote ((x)(x)), then the three bracketings of three entities can be written as

where B_j,k signifies the kth bracketing of j entities. Likewise we can write the eleven bracketings of four entities as

Thus, letting s_n denote the number of distinct bracketings of n entities, we have s₁ = s₂ = 1, s₃ = 3, and s₄ = 11. Now consider the function g(z) defined as

Raising this to the powers 2, 3, 4, 5, … we get

and so on. The coefficient of z^k in g(z)² is the numbers of distinct ways (including different orderings) in which two terms whose indices sum to k can be multiplied together, and the coefficient of z^k in g(z)³ is the number of distinct ways in which three terms who indices sum to k can be multiplied together, and so on. Since each s_n signifies the number of bracketings of n entities, it follows that if we sum all the polynomials and collect by powers of z we get

in which the coefficient of z^k is the number of distinct ways of bracketing k entities. This is just the definition of s_n, so we need only add s₁z = z to this sum of powers of g(z) to give the original g(z). Thus we have

Solving this for g(z) gives the generating function

The notation for representing bracketings can be simplified in various ways. For example, we can let u denote (x), in which case the bracketing of two entities can be written as (u²), and the three bracketings of three entities can be written as (u³), (u(u²)), and ((u²)u), and the eleven bracketings of four entities can be written as

The base symbol “u” is somewhat redundant, since only the exponents are significant, so we could also write these same bracketings in the form

Such bracketings can also be represented as branching tree structures. For example, the 11 bracketings of 4 entities correspond to the trees shown below.

We refer to the values of s_n as “small Schröder numbers”, the first several values of which are

Naturally the fact that s₁₀ equals Hipparchus’ number of “connections” of 10 items has led to speculation that Hipparchus was actually calculating something like the number of bracketings. The equality of these numbers, both for the index 10, certainly lends support to this idea – assuming the other value quoted by Plutarch, i.e., 101049, was just a misprint. At the very least it suggests that Hipparchus was calculating something meaningful. On the other hand, it isn't obvious that "bracketing" means the same thing as "connections", let alone the same thing as "compound propositions", since the latter would usually be taken to signify logical statements, with the elements (axioms) connected by set-theoretic operations (“and”, “or”, etc.). This interpretation of the context is re-enforced by the reference to both affirmative and negative propositions.

Regarding logical propositions, it might be worth noting a closely related sequence, sometimes called the large Schröder numbers, whose values (except for the first) are simply twice the values of the small Schröder numbers. By convention we set S₁ = 1 and S_k = 2s_k for all k greater than one. Thus the first ten values of this sequence are

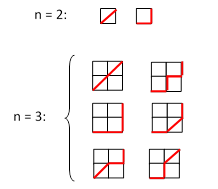
The large Schröder numbers arise in several different contexts. For example, S_n is the number of paths from one corner of a square lattice of size (n−1) x (n−1) to the opposite corner, moving only north, west, or northwest, and never rising above the diagonal. These paths are illustrated below for n = 2 and n = 3.

Notice that each pair of side-by-side paths are “duals” of each other, in the sense that each diagonal segment is replaced by an east-north pair of segments, and vice versa. This duality explains why the small Schröder numbers (i.e., half the large Schröder numbers) arise so commonly.

Another appearance of the large Schröder numbers – and one that might have some relevance to Hipparchus’ statement – is the number of certain compound statements in Boolean logic. It seems unlikely that Hipparchus would have regarded the axioms as indistinguishable entities, so rather than considering the bracketings of a string of “x” symbols, we might consider n distinct entities a, b, c, … (Of course, since the order of these entities remains unchanged in the propositions, their identities can be established by their positions, so we don’t generalize the situation by assigning unique designations.)

With the usual Boolean notation conventions we can write the possible logical propositions (without negation) on an ordered string of n simple axioms a,b,c..., for n = 1, 2, 3, and 4, as shown below.

The number of expressions without parentheses is 2ⁿ⁻¹, since we have the binary choice of whether or not to place a “+” symbol in each of the n−1 locations between two adjacent characters. We then generate modified versions of these basis expressions by placing parentheses in all possible ways to give distinct sums of products (based on the usual distributive property). Thus with n = 5 we will have the 2⁴ = 16 basic connections, eight of which are given by appending the fifth character “e” to each of the basic expressions for n = 4, and the other eight of which are given by appending “+e” to the basic n = 4 expressions. Given the 16 basic expressions for n = 5, we then form all possible parenthetical modifications. The table below lists the parentheticals for the basic expressions beginning with “ab”, because (as will be discussed shortly) there is a one-to-one correspondence between these as the parentheticals for the basic expressions beginning with “a+b”.

There are 45 expressions listed in this table, each giving a distinct sum of products. Now, it’s easy to see that there will be the same number of parentheticals for a+bcde as there are for abcd+e, since these are mirror images of each other, but perhaps less obvious is the general duality between “sums” and “products” (i.e., between “and” and “or” operations). Take for example the basic expression ab+c+de and its parentheticals. We can place these in one-to-one correspondence with the parentheticals of the dual expression a+bcd+e as shown below.

In each case we simply exchange products and sums. The pattern is the same as that given by negating each expression in the left hand column and then expanding using De Morgan’s rules into an expression in terms of the individual negated entities, which we then treat as the original entities. Therefore, the total number of expressions for N = 5 is twice the number of expressions beginning with “ab” (because we have the same number beginning with “a+b”). Hence for N = 1, 2, 3, 4, and 5 elements we have 1, 2, 6, 22, and 90 compound statements respectively. These of course are the large Schröder numbers, and so the number of such expressions for N = 10 elements is 206098, which is exactly twice Hipparchus' “affirmative” number. But since these expressions are symmetrical because of the duality between sums and products just described, the number of distinct "connections" for ten axioms, up to this duality of “and” and “or” operations, is 103049. Thus it’s conceivable that Hipparchus might have had something like these compound Boolean statements in mind.

Incidentally, the above expressions are what's called "monotonic", meaning that they don't involve any negations of the basic elements. Dedekind’s Problem is to determine the number of monotonic Boolean expressions in n variables, but of course it doesn’t require the basic elements to be ordered as they are in the expressions above. As a result, the total number of monotonic expressions in n variables grows much more rapidly than the Schröder sequences. Nevertheless, there could be a relation between the "affirmative statements" of Hipparchus and what we call monotonic Boolean functions.

Assuming Hipparchus and the other ancient mathematicians meant something like the bracketings or logical Boolean propositions described above when they referred to “the number of compound propositions on n axioms”, it would be very interesting to know how they actually computed the Schröder numbers. The calculations themselves would have been challenging enough, but in addition it would have taken some fairly sophisticated combinatorial reasoning to derive an efficient formula. This is especially intriguing because no significant tradition of algebraic combinatorial analysis has survived in the extant writings of ancient mathematicians. For example, there is no reference in ancient Greek or Roman literature to even such elementary concepts as the binomial coefficients, and yet here we seem to find Hipparchus able to compute the 10th Schröder number!

It’s conceivable (just barely) that some ancient mathematicians might have just stumbled into the convolution formula for either the large or small Schröder numbers. From the recursive definition of operations involving n entities, it’s natural to suspect that these operations would consist of all the “products” of operations involving fewer entities. For example, letting B_k denote the set of expressions on k entities, we would expect (roughly speaking) that B₅ consists of the union of the Cartesian products

and therefore we might guess that S₅ should be the corresponding convolution of S₁ through S₄. Now, it so happens that this gives the value 68, which is 22 less than the true value of S₅. But they could have noticed that S₄ = 22, so they might have surmised the (correct) formula

It’s easy to verify, as shown below, that this does indeed give the correct values of S₂ through S₅, all of which can also be worked out by inspection.

Similarly the values of each small Schröder number differs from twice the convolution of lower numbers by the value of the previous number, which is to say they satisfy the convolution recurrence

The idea that ancient mathematicians might have used guess-work and incomplete induction to arrive at results may seem surprising, given the emphasis they (especially the Greeks of the classical period) placed on rigor, but this may be precisely the reason none of their algebraic and combinatorial results were preserved. They might not have regarded this kind of reasoning as legitimate mathematics. It’s tempting to think they may have proceeded along these lines to find this isolated result (like Balmer guessing the formula for the spectral lines of the hydrogen atom), but on the other hand, I’m not aware of convolutions being used by ancient mathematicians. (For an explanation of how those convolution recurrences, as well as the direct second-order recurrence discussed below, can be derived, see the note on Generating Functions and Recurrence Relations.)

They did, however, make frequent use of recurrence relations (a technique dating back to the ancient Babylonians) for computing square roots and other algebraic quantities. Thus, in the spirit of speculating about what disreputable reasoning might have led some ancient mathematician to the 10th Schröder number, it’s only mildly far-fetched to imagine that they might have tabulated the initial values of the sequence s_n along with some common recurrence functions as shown below.

From this one could guess that the right-hand column is always 3/n, so in general s_n is given by

Of course, they wouldn’t have noted that this implies that the Schröder numbers have a simple generating function (as discussed above), but they have noticed that this recurrence implies that the Schröder numbers have some interesting divisibility properties. To illustrate, we can define what might be called “extra large Schröder numbers” as 3 times the basic Schröder numbers. Letting S_n = 3s_n denote this sequence of values, the table below shows the first several values along with their residues modulo n.

From the preceding recurrence relation we also have the congruence

The Schröder numbers also have the interesting property that s_n is divisible by n if n is a prime (other than 2), whereas s_n is not divisible by n for any composite n less than 100. In fact, among the integers less than 1000, the only odd composite integers n such that s_n = 0 (mod n) are 105, 261, 301, and 693. The only one of these not divisible by 3 is 301. When searching for such “Schröder pseudoprimes”, it’s convenient to make use of the convolution formula rather than the second-order recurrence, because the latter involves divisions by each integer up to n, whereas the former involves nothing but multiplications and additions, which can easily be carried out modulo n for any integer n.

Incidentally, from the generating function for the Schröder numbers we can derive (by repeated differentiation) an interesting recurrence that closely resembles the recurrence relations for the Bernoulli numbers, and even mores the recurrence relation for the Eulerian numbers. Letting σ_n denote the small Schröder numbers, re-indexed for convenience so that σ₀ = 1, σ₁ = 3, σ₂ = 11, σ₃ = 45, and so on, we have

This can be used to easily compute the values of σ_n, and like the convolution formula (but unlike the second-order recurrence) it requires no divisions. Two peculiar aspects of this formula are the appearance of the number 3 as the argument of the left hand polynomial, and the fact that this polynomial has such different values for odd and even values of n. It also shows the close relationship between the Schröder numbers and the Catalan numbers (from the appearance of the central binomial coefficient on the right side). The first few values of the right hand side for n = 2, 4, 6, 8, 10, and 12 are 2, 8, 40, 224, 1344, 8448. Interestingly, the left hand polynomial has a root with real part equal to 3 for all indices n, but when n is even the root has an imaginary part. We also note that the number 3 appears as the argument of the Legendre polynomials P_n(x) in the well-known formula for the small Schröder numbers

As an example, the 5th and 6th Legendre polynomials are

and so the small Schröder number s₆ can be computed as

One might think that the Legendre polynomials give the minimal family of polynomials for the small Schröder numbers, but in fact we can derive a simple family of polynomials of lower degree that give the same values. Making use of the formula (1), we can derive the following expressions for the small Schröder numbers.

The coefficients in each row can be determined from those above it using the alternating binomial recurrence of order equal to the row number. Expressing the coefficients explicitly in terms of binomial coefficients, we find that the small Schröder numbers s_n = σ_n−2 are given in closed form by

The above discussion has focused on the first of the two numbers quoted by Plutarch, representing the number of “affirmative” connections. It isn’t clear what he (or Hipparchus) meant by the distinction between affirmative and negative connections or propositions. If we allow negations of the variables (but still require the elements to be ordered as above), then the number of possible expressions will certainly be much larger even than the number 310,952, so it isn't clear where this number of "negative statements" is supposed to signify. It seems strange that the quoted number for negations is so close to three times the affirmative number, i.e., 310952  =  3(103049) + 1805. It's hard to think of introducing negation could just increase the number of possible expression by a factor if 3. We can almost imagine Hipparchus negating each of the above monotone expressions and then applying something like De Morgan's rules to express them as direct statements in the negated elements, but it seems this should just give the same number of negative expressions as affirmative expressions.

It's been suggested that Hipparchus might have meant 310954 (i.e., two greater than the value quoted by Plutarch), since this number has some combinatorial significance. However, the connection of this number to what can plausibly be called "negative compound propositions" is not very strong, and it requires us to believe that Plutarch mistakenly quoted the same wrong value in two different essays. So the "negation" number 310952 is still mysterious, but the fact that the "affirmative" number 103049 has a valid foundation makes it all the more tantalizing, since it clearly suggests that Hipparchus knew some non-trivial combinatorics. Also, it seems unlikely that these results were produced in isolation. There must have been a body of combinatorial knowledge circa 150 BC that has not come down to us.

Incidentally, Chrysippus (280-206 BC) is reputed to have had a genuine scientific interest in propositional logic, and wrote over 300 works on the subject. Despite the interest in the numbers reported (in somewhat garbled form) by Plutarch in refutation of Chrysippus, it’s worth noting that Chrysippus was actually correct, at least for some reasonable definitions of “compound propositions”. In fact, when he said the number of positive compound propositions that can be formed from just 10 axioms “exceeds a million” he was actually under-stating the case. The number of distinct monotone Boolean expressions on 10 variables is estimated to be (8.5)10⁷⁸, which coincidentally is also a rough estimate for the number of atoms in the universe.

Return to MathPages Main Menu