|
Are All Triangles Isosceles? |
|
|
|
Euclid's great synthesis of Greek geometry, The Elements, was for centuries regarded as a model of abstract axiomatic reasoning, but in the 19th century a close examination of the foundations of mathematics led to the realization that Euclid's axiomatic structure is actually quite deficient in many respects. In particular, it never clearly defines some important fundamental concepts such as "betweenness" and "continuity". In retrospect it's clear that Euclid's geometry, rather than giving rigorous proofs of abstract concepts suggested by roughly drawn figures, actually gave rough intuitive proofs based on accurately drawn figures. |
|
|
|
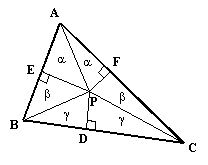
One well-known illustration of the logical fallacies to which Euclid's methods are vulnerable (or at least would be vulnerable if we didn't "cheat" by allowing ourselves to be guided by accurately drawn figures) is the "proof" that all triangles are isosceles. Given an arbitrary triangle ABC, draw the angle bisector of the interior angle at A, and draw the perpendicular bisector of segment BC at D, as shown below: |
|
|
|
|
|
|
|
If the angle bisector at A and the perpendicular bisector of BC are parallel, then ABC is isosceles. On the other hand, if they are not parallel, they intersect at a point, which we call P, and we can draw the perpendiculars from P to AB at E, and to AC at F. Now, the two triangles labeled "alpha" in this figure have equal angles and share a common side, so they are totally equal. Therefore, PE = PF. Also, since D is the midpoint of BC, it's clear that the triangles labeled "gamma" are equal right triangles, and so PB = PC. From this it follows that the triangles labeled "beta" are similar and equal to each other, so we have BE+EA = CF+FA, meaning the triangle ABC is isosceles. |
|
|
|
Of course, if we attempt to accurately construct the points and lines described in this proof we will discover that the actual configuration doesn't look like the figure above. The point P necessarily falls outside the triangle ABC. However, if we carry out the proof on this basis, and if we now assume the points E and F also fall outside the triangle, we still conclude that the triangle is isosceles. This too is an incorrect configuration. |
|
|
|
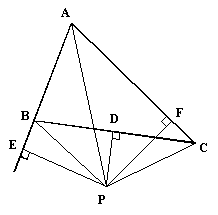
The actual configuration of points given by the stated construction is for the point P to be outside the triangle ABC, and for exactly one of the points E,F to be between the vertices of the triangle, as shown below |
|
|
|
|
|
We still have AE=AF, PE=PF, and PB=PC, and it still follows that BE=FC, but now we see that even though AE=AF and BE=FC it does not follow that AB=AC, because while F is between A and C, E is not between A and B. This illustrates the importance of "betweeness" as a concept in geometry. M. Pasch was among the first to point out the importance of "axioms of order" to establish the meaning of this concept, in his "Vorlesungen uber neuere Geometrie" (1882). Hilbert incorporated them into his "Foundations of Geometry" |
|
|
|
Coincidentally there was a lengthy discussion on the internet not long ago concerning the question of whether Euclid's Elements, viewed as a formal axiomatic system, was fundamentally sound and logically consistent. It was mentioned that there are many serious flaws in "The Elements", such as the free use of "superposition" to establish congruence results (which is based on pure physical intuition of moveable material objects and has no hint of justification within Euclid's axiom system), the many implicit assumptions of continuity (which are not even acknowledged, let alone formalized, in "The Elements"), the meaninglessness of most of the "definitions" (many of which are never subsequently used), and the complete absence of axioms of order and "betweenness", thereby allowing numerous false "proofs" such as the one described above. |
|
|
|
Oddly enough, although the defects in Euclid's "Elements" are common knowledge among historians and philosophers of mathematics, they seem to be largely unknown to many working mathematicians, who continue to regard "The Elements" as a model of axiomatic rigor (which, arguably, it was never even intended to be, since the Greek geometers probably considered themselves to be engaged in what we today would call physics, rather than axiomatics). |
|
|