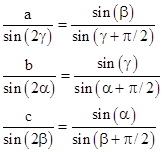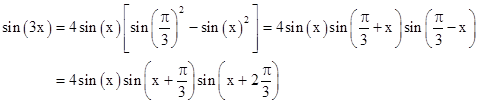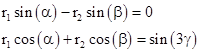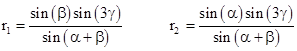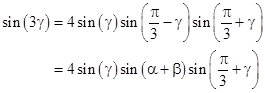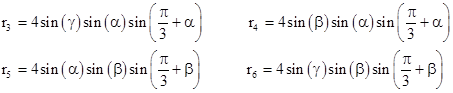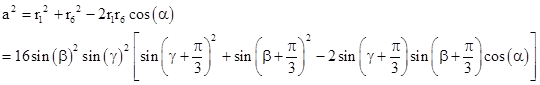Morley's Trisection Theorem

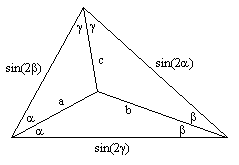
In Proposition 4 of Book IV of the Elements, Euclid inscribes a circle inside an arbitrary triangle by showing that the bisectors of any two of the interior angles meet at a point equidistant from the three edges.  Since there is only one such point, it follows that the bisectors of all three angles meet at the same point.  Letting 2α, 2β, and 2γ denote the three interior angles of a triangle, the law of sines implies that the edge lengths are proportional to the sines of these angles, so we can scale the triangle to make the edge lengths equal to these sines as shown below.

Since α + β + γ = π/2, the central angles are γ + π/2, β + π/2, and α + π/2, and the law of sines gives the ratios

Making use of the double-angle formula

we can substitute for the sines of 2γ, 2β and 2α in the previous ratios and simplify to give

Hence by the sine rule we see that the point of intersection is a distance of

from each of the three edges, which confirms that this point is the center of the inscribed circle.

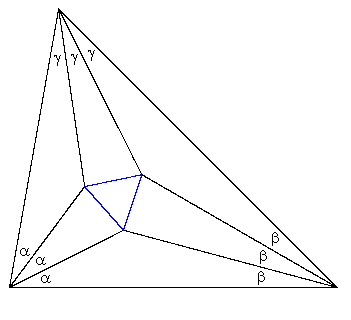
Now, since the bisectors of a triangle meet at a single point (a fact which is not entirely self-evident), it seems natural to go on to consider how the trisectors of a triangle meet.  However, Euclid apparently didn't consider this question, nor did anyone else for over 2000 years.  (Of course, it's impossible to trisect an arbitrary angle using Euclidean methods, i.e., by straight-edge and compass, so Euclid obviously couldn't have used trisectors in any constructions, but he could still have proven some interesting theorems about trisectors if he had wished.)  It wasn't until 1899 that Frank Morley (one time was president of the American Mathematical Association) discovered that lines trisecting the angles of an arbitrary plane triangle meet at the vertices of an equilateral triangle as illustrated in the figure below, where the central triangle (in blue) is equilateral.

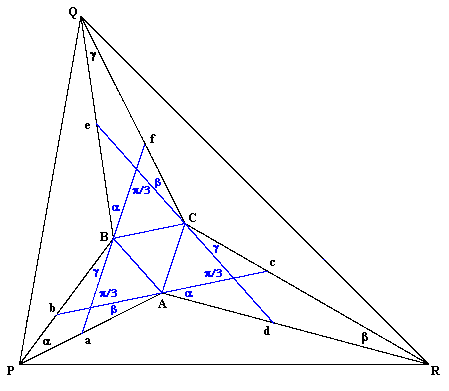
At first it may not be obvious why this proposition is true, but it can be proven very simply by showing that, beginning with an equilateral triangle, we can construct an encompassing triangle with arbitrary interior angles 3α, 3β, 3γ (summing to π) such that the lines from the vertices of this new triangle to the vertices of the original triangle trisect the interior angles of the former.  Since the construction is unique, this is sufficient to prove that the trisectors of an arbitrary triangle meet at the vertices of an equilateral triangle.  The construction is fairly simple, and could easily have been found by the ancient Greeks if they had considered such problems.  We begin with the equilateral triangle marked ABC as shown in the figure below.

Then we construct the line bAc parallel to BC, and aBf parallel to AC, and dCe parallel to AB.  Now, for any given angles α,β,γ, draw a line through point A making an angle of β with the line Ab, and draw a line through B making an angle γ with the line Ba.  Let P denote the intersection of these two new lines.  Likewise we can construct the point Q and R using the angles α,β and α,γ respectively, as shown in the above figure.  By construction the angles APB, ARC, and BQC are α, β, and γ respectively.  Furthermore, the triangles PbA and AcR are similar, and the segment Ab equals the segment Ac, which implies that the corresponding edges are in the ratio of Pb to bA, and hence the bases are in this ratio, so the triangle PAR is also similar to these two (noting that the angle at A is π – α – β).  As a result the angles APR and ARP are α and β respectively.  By the same reasoning, the angle BPQ and CRQ are α and β respectively, and the angles BQP and CQR are both γ, so we have constructed the desired triangle whose angle trisectors meet at the vertices of the equilateral triangle ABC.  Naturally the result can be scaled arbitrarily, so the proof is complete.

The above proof requires nothing beyond Euclidean constructions and propositions, but it represents only an existence proof.  It doesn't enables us, given an arbitrary triangle PQR, to construct the equilateral triangle ABC.  Instead, the proof works in reverse, which is sufficient to prove that the equilateral triangle ABC exists for any PQR, even though we can't construct it (by straight-edge and compass).  The ancient Greeks certainly made free use of indirect proofs (recall Euclid's non-constructive proof of the infinitude of primes), and they could easily have proven Morley's Theorem, but they apparently never noticed it.  It's often said that the Greeks didn't consider propositions involving trisections because of the impossibility of trisecting an arbitrary angle by Euclidean methods, but in fact the Greeks developed numerous methods for trisecting angles, based on higher degree curves, so this doesn't fully explain why they never noticed Morley's theorem.

From the modern perspective, we can use trigonometry to develop a direct constructive proof as well.  First, it's worthwhile to review why an angle trisection cannot be accomplished by straight-edge and compass methods.  Such methods are capable of any quadratic constructions, i.e., constructions corresponding to the solutions of polynomials of degree 2.  Obviously these methods are adequate to bisect any arbitrary angle, because a bisection corresponds to solving the trigonometric identity sin(2x) = 2sin(x)cos(x), which can be done purely by quadratic steps by means of the equation

In contrast, given sin(3x), the determination of sin(x) involves the solution of the irreducible cubic

so it cannot be done by quadratic methods.  Incidentally, this expression implies the existence of a triple-angle formula analagous to the double angle formula

discussed previously.  The triple-angle equation can be analyzed as follows

The quantity in the square brackets is the difference between two squared sines if we replace 3/4 with the square of sin(π/3).  Then we can use the identity sin(u)² – sin(v)² = sin(u+v)sin(u–v) discussed in the note on Napoleon's Theorem, and arrive at the result

In general, it's easy to show by means of the exponential forms that the value of sin(nx) for any n can be expressed as the product of n sines

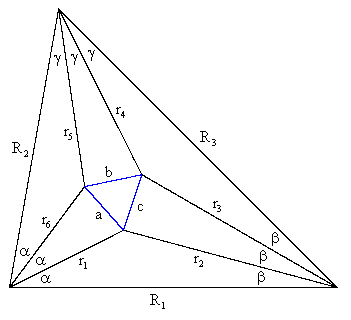
The product form for the triple angle is particularly useful in developing a direct constructive proof of Morley's theorem.  Let's begin with an arbitrary triangle with interior angles 3α, 3β, and 3γ as shown below.

We first apply the Rule of Sines to scale the overall triangle so that R₁ = sin(3γ), R₂ = sin(3β), and R₃ = sin(3α).  Then, focusing on the triangle with edges R₁, r₁, and r₂, we have the relations

Solving for r₁ and r₂ gives

At this point we want to eliminate the triple angle, so we make use of the triple-angle identity

where we have substituted α+β for π/3 – γ.  With this we can re-write the lengths r₁ and r₂ as

Likewise the lengths of the other trisecting segments are

Now, by the Law of Cosines we know that the squared edge length a² of the triangle that we claim is equilateral is given by

Notice that the angles of the triangle with edges r₁, a, r₂ are α, γ + π/3, and β + π/3, so the edge lengths are proportional to the sines of these angles.  Therefore, the quantity in the square brackets is simply sin(α)², and so we have

which is symmetrical in the three angles.  Hence the squared lengths b² and c², have this same value, proving that the triangle is equilateral.

Incidentally, by drawing such figures it might appear visually that the center of the equilateral triangle given by Morley's theorem coincides with the center of the inscribed circle of the original triangle, but they are actually not exactly coincident.

Return to MathPages Main Menu