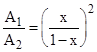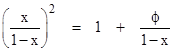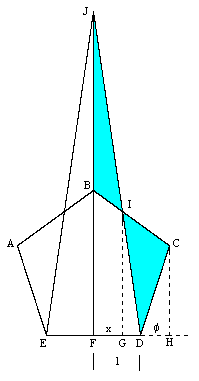
Pent Up Ratios

Construct an isosceles triangle on one edge of a regular pentagon in such a way that the areas of the triangle and pentagon are equal, as shown below.

The point I cuts both BC and DJ in the golden ratio. This follows immediately from the fact that, since the areas of BIJ and CID are equal, and the angles at I are equal, we have |BI|×|IJ| = |CI|×|ID|. Choosing the scale so that |FD|=1, and letting x and ϕ denote the lengths of the segments FG and DH, this gives x/(1+ϕ) = 1−x and therefore x = (1+ϕ)/(2+ϕ). An elementary fact about regular pentagons is that ϕ is the golden ratio, i.e., we have

Substituting this into the expression for x gives

Hence we have x = ϕ and therefore (1−x)/x = ϕ, so by projection it follows that |BI|/|IC| and |DI|/|IJ| both equal ϕ, which was to be shown.

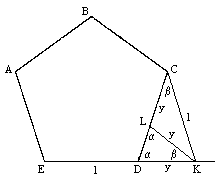
We have made use of the elementary fact that |DH|/|FD| = ϕ. For completeness, we can prove this by drawing another line segment of length |CD| from the point C to the point K on the extended line ED as shown below. For convenience we now take |ED| = 1, and we wish to show that y = |DK| in the figure below is equal to ϕ.

Since the main figure is a regular pentagon, the angle KDL is α = 2π/5 (i.e., 72 degrees), and since DCK is isosceles, the angle CKD is also 2π/5, which implies that the angle DCK is b = π/5. Now we construct the line of length KD from the point K to the line DC at L. The triangle DKL is isosceles, so the angle DLK equals α = 2π/5 and the segment |KL| equals y. This also implies that the angle DKL is β = π/5, and therefore so is the angle LKC, which shows that the triangle KLC is isosceles, implying that the line segment |LC| equals y. Then, since |DC| = 1, it follows that |LD| = 1 − y. Now, by similar triangles we have y/1 = (1−y)/y, and hence y² + y − 1 = 0, whose positive root is ϕ, which was to be shown.

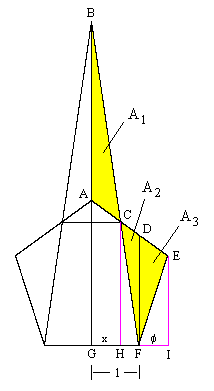
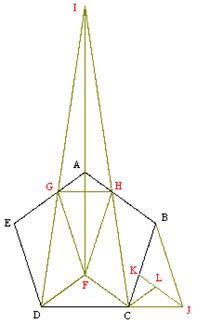
Incidentally, the assertion that |BI|×|IJ| = |CI|×|ID| essentially expresses the fact that the dot product of two vectors equals the product of their magnitudes times the sine of the angle between them, and this equals the area of the parallelogram which they describe. An alternative, and perhaps more elementary approach to the original proof can be based on the figure below.

We've drawn the vertical line FD. Letting by A₁, A₂, and A₃ denote the areas of the triangles ABC, DFC, and DEF respectively, we have A₁ = A₂ + A₃. Also, the triangles ABC and DFC are similar, so their areas are proportional to the squares of their widths, i.e.,

Furthermore, triangles CDF and DEF share a common base, so their areas are directly proportional to their widths, i.e.,

Dividing the equation A₁ = A₂ + A₃ by A₂ and substituting for these ratios gives the relation

Solving for x, we arrive at x = (1 + ϕ)/(2 + ϕ), just as in the original proof.

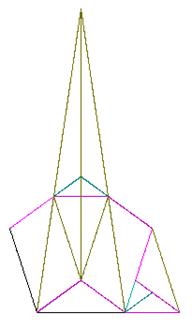
Both of the preceding proofs rely on some algebraic steps. To express a proof in purely geometrical form, consider the figure below.

Clearly the point I that makes the area of ICD equal to the area of the pentagon ABCDE is unique, so if we construct this point by some other means (that makes the equality of GH and CJ obvious) and then show that the areas IHA and HBC are equal, the proposition will be proven. So, beginning with the pentagon ABCDE, let F denote the intersection of the lines through C and D parallel to BA and EA respectively. Then let G (resp H) denote the intersection of AE (resp AB) with the line through F parallel to ED (resp BC). Finally, let K denote the intersection of BC with the line through J parallel to AB, and let L denote the intersection of JK with the line through C parallel to EA.

Clearly GH equals CJ, so we need only show that the area of IHA is equal to the area of HBC. Those two triangles share a common angle at H, so their areas are equal if and only if |HC|/|HI| = |HA|/|HB|. Now, by construction, the triangles CFI and HAI are similar, so we immediately have |HC+HI|/|HI| = |CF|/|HA|. Also, we have |HA| = |CL| = |CK| as well as |CF| = |HB| = |BK| = |KJ| = |JC|. In addition, we have |JC|/|CK| = |BK+CK|/|CJ|. Hence the ratio |CF|/|HA| can be written as |HA+HB|/|HB|. As a result, we have |HC+HI|/|HI| = |HA+HB|/|HB|, which implies that |HC|/|HI| = |HA|/|HB|.

The figure below illustrates the common lengths that are exploited in the proof.

Incidentally, the point I is also the apex of the regular pentagon constructed on the base BE. In addition, the point I lies on the extension of the line JB. Of course, from the fact that IDC has the same area as the pentagon, it follows that the height of point I above the base DC is five times the height of the center of the pentagon ABCDE.

Return to MathPages Main Menu