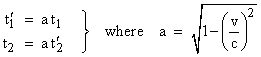Herbert Dingle and the Twins

That is, in essence, the central meaning of relativity. It takes us to the view-point of the Gods, from which we see things as they are, unmodified by reflection in matter, space, and time. It is a step towards truth, and truth is simple to the simple-minded.

                                                                                                      H. D. Dingle, 1922

A succinct explanation of Herbert Dingle’s alleged paradox involving special relativity was given in another note, but some readers have commented that a slightly less succinct explanation, preferably one that does not mention partial derivatives, would be welcome.

To set the stage, recall that, after his retirement in 1955, the cantankerous British “philosopher of science” Herbert Dingle (1890-1978) embarked on a campaign against Einstein’s special theory of relativity. Dingle himself had written on the subject in earlier years, notably in his 1922 essay “Relativity for All” and his short 1940 monograph “The Special Theory of Relativity”. In these and other writings he expressed approval of what he understood to be special relativity, but, ominously, these writings also reveal that he profoundly misunderstood it. This misunderstanding came to the forefront in the late 1950’s when he began writing letters to the editors of various science magazines (especially Nature) to inform the world that, contrary to widespread belief, special relativity did not predict asymmetric ages for the hypothetical twins in the famous “twin paradox” (when one twin moves inertially and the other travels out and back). After much acrimonious debate, Dingle finally conceded that he was wrong. One can hardly imagine how embarrassing and humiliating it must have been for a man who had written about and lectured on a subject for his entire career to have such an elementary misunderstanding of that subject publicly exposed as he approached his 70th birthday. (As a personal aside, his sense of isolation during these years was increased by the loss of his wife 12 years earlier.)

Dingle’s reaction was to convince himself that, since he hadn’t understood special relativity, it must be because special relativity didn’t make sense. Over the next two decades, until his death in 1978 at the age of 88, he devoted himself to discrediting the theory, arguing (in articles and letters to magazine editors) that special relativity was not just empirically wrong (as in its prediction of asymmetric aging, which he still suspected to be false in nature), but logically self-contradictory. With each new claim, he revealed more clearly how utterly he had always failed to understand the subject, and this in turn hardened his conviction that the theory was simply self-evident nonsense. By the time he reached the age of 80, few magazine editors would agree to publish any more of his letters, and his old colleagues had long since decided that the kindest thing to do was to simply let his rants pass in silence. This convinced Dingle that there was a giant conspiracy in the “physics establishment” to silence him, and that all scientists were either complete idiots or else lacked the intellectual integrity to admit they were wrong, preferring to acquiesce in the world-wide pro-relativity conspiracy.

Ironically, Dingle’s earliest objections (during the years when he still believed relativity to be “sound”) could have been construed as raising genuine issues about the origin of inertia, which is acknowledged as an epistemological weakness of special relativity, and which remain unresolved even in the context of general relativity. However, Dingle strenuously rejected any such interpretation of his objections. He even went so far as to argue that questions about the “origin of inertia” are senseless and stupid. As far as he was concerned, inertia simply is, and it could not be otherwise. He insisted that the problem with special relativity was not simply any epistemological shortcoming, but that it was logically impossible. He came to focus his technical criticism of special relativity on one particular scenario, which he claimed was proof that special relativity entails a self-contradiction. As preposterous as this claim is, it continues to be espoused by some modern-day anti-relativityists, who even today carry on Dingle’s crusade against the pro-relativity conspiracy. Hence the relevance of explaining the fallacy of Dingle’s argument, even though objectively it is so trivially wrong that it wouldn’t merit any discussion.

Dingle’s “logical contradiction” was described most famously in an exchange of letters published together with the astrophysicist W. McCrae in an issue of Nature in 1967. He asked his readers to consider four identically constructed clocks, denoted as N, B, A, and H, all located along a single straight line. The clocks A and H are mutually at rest relative to each other, as are the clocks N and B. These two pairs of clocks are in motion relative to each other. Specifically, clocks N and B are moving in tandem to the right, and clocks A and H are moving in tandem to the left, so the pairs are (initially) approaching each other with the mutual speed of v. Dingle stipulated that clocks A and H were to be synchronized with each other using the method described in Einstein’s 1905 paper, i.e., if a light pulse is emitted from A at time T₁, reflected from H at time T₂, and received back at A at time T₃, then the clocks are considered synchronized if T₂ = (T₁+T₃)/2. In other words, when clock H is struck by the light, it is set to the average of the times of emission and reception on clock A. By the same method clocks B and N were to be synchronized with each other.

Now, in the obscure one-dimensional quasi-verbal mode of expression that is the hallmark of anti-relativityists, Dingle identifies what he calls three specific “events” as follows:

The following are three successive events during the process.

N B t’=0

A t=0     H        (Event E₀)

Here B is adjacent to A, and both are observed to read 0.

N B t’=t1’

A H t =t1     (Event E₁)

Here H is adjacent to B, H is observed to read t₁ and B to read t₁’.

N t’=t1’       B

A t =t1    H         (Event E₂)

Here A is adjacent to N, A is observed to read t₂ and N to read t₂’.

Already at this point the fallacy is clear, as is Dingle’s complete failure to understand the first thing about special relativity. What he calls an “event” is actually more like a classical “instant”. This misconception, which might seem innocuous to someone unfamiliar with special relativity, totally undermines his attempt at a coherent formulation of his “paradox”, so it’s worth examining his mistake in some detail. Notice that his “event E₀” is not just the coincidence of clocks A and B, it includes clocks N and H at their respective locations as well. But of course those clocks are spatially distance from the point where A and B are located, so the aggregate of all these clocks is not an event at all. Notice that Dingle hasn’t even assigned times to clocks N and H in what he calls “Event E₀”, nor (of course) has he quantified the distances. All of this just illustrates both the hopelessness of trying to capture all the relevant information in this obscurantist anti-relativityist format, and Dingle’s appalling misunderstanding of the word “event” as it is used in the theory he is supposedly trying to analyze. In addition, notice that Dingle has specified that the three so-called “events” are successive, which of course pre-supposes an absolute ordering of spatially separate events which is essentially the very thing he is trying to prove. His entire specification is shot through with misunderstandings, inconsistent definitions, and false premises… and we haven’t even gotten to his argument yet!  Revealingly, Dingle comments dryly at this point

All this is quite independent of theory: it is a simple physical description of a possible physical process.

Such an insipid claim from a man who fancied himself a philosopher of science is astonishing. Evidently Dingle never so much as suspected that his garbled mess already contained several theory-laden presumptions, which would be sufficient to falsify the claim of theory-independence even if those presumptions weren’t utterly non-sensical (which unfortunately they are).

At this point we can’t avoid asking how it is possible for Dingle, who wrote books purporting to explain the special theory of relativity to the public, to be unaware of the meaning of the word “event” within that theory. Granted, he was 77 years old when he wrote this, so it wouldn’t be surprising if he was past his intellectual prime. But still, could a man simply forget something so fundamental – while still being capable of forming complete sentences? It seems hard to believe. The resolution of this mystery is to be found in Dingle’s earlier writings on special relativity, extending all the way back to 1922, and on up through his 1940 monograph. We find that the word “event” appears more often than any other single word in his 1922 essay, and indeed he stressed the importance of the concept of the “event” in special relativity, almost to the point of being ridiculous. For example, he says

The new point of view is of especial interest because it suggests the possibility of a more complete unification of Nature than any previously imagined. With one hand relativity destroys the throne of matter and motion: with the other it erects an altar to the event… if we start with the event, there is only one deity on our Olympus…. Two observers of Nature see, not necessarily the same matter, but the same events, because events finally constitute the external physical world…

Dingle had obviously heard that the “event” was a basic idea in relativity, so he was trying to exalt it, but we can already see that his conception of the term is fundamentally wrong when he says that two observers see the same events. He goes on to explain his understanding of the “event” is more prosaic terms:

Let us illustrate this point, which is of basic importance, by an example… Consider two events: first, a young man sees a young maiden; second, he shows signs of agitation. Consider, further, two observers of these events the young man himself and another young maiden. Each of them relates the events in a certain way. The young man calls his relation "love"; the second young maiden supposing she is honest with herself calls her relation "jealousy." Here, then, we have a type of relation between events which we definitely recognize as relative.

Thus he is already in 1922 conceiving of an “event” as something like the normal verbal usage of that term, such as when he says a young man seeing a young maiden is an “event”. Mind you, the “event” as Dingle conceives it is not just “the man seeing”, because the other maiden’s reaction to observing this “event” is jealousy, so it’s clear that the “event” Dingle has in mind includes not just the man seeing but also the maiden being seen. Granted, his words are vague enough that one might, with charity, have thought it best to give him the benefit of the doubt, presuming that perhaps he just chose a not very apt analogy, but in the light of his later writing we can see in retrospect that his thinking really was as confused and misguided as it seemed. He clearly never understood that an “event” in special relativity is one particular time and place, no more and no less. We might expect to find that he had understood this at least by the time he wrote his monograph on special relativity in 1940 but, remarkably, we find that the word “event” does not appear even once in this book. (As an aside, the word “Einstein” never appears in the book either, a fact which Dingle acknowledged and regretted in the preface to the fourth edition… along with the announcement that he had by then discovered that special relativity was nonsense.) So, he never learned what the word “event” means in special relativity to begin with, and by the 1940’s he had expunged the term from his working vocabulary (along with the word Einstein), and it reappeared in his writing only in retirement, when his usage of it betrayed the fact that he had never understood its meaning. It’s literally accurate to say that Dingle never knew the first thing about relativity.

The source of Dingle’s conception of the “event” was evidently the mathematician and philosopher Alfred North Whitehead, acknowledged by Dingle in “Relativity for All” as the person who taught him “relativity”. As noted elsewhere, Whitehead was actually an opponent of Einstein’s theory, and advocated his own alternative theory. Newman summarized a key aspect of Whitehead’s philosophy of science as follows:

He rejected, in Whittaker’s words, the accepted starting point of physics, “namely, that space and time provide, so to speak, a stage on which ponderable bodies , aether and electricity maintain an unending performance. In place of this he put forward the doctrine that the ultimate components of reality are events.”  Every event… includes other events and is itself included in larger, more comprehensive aggregates. Time and space enter into this world as “derivative concepts… abstractions which express relations between events”.

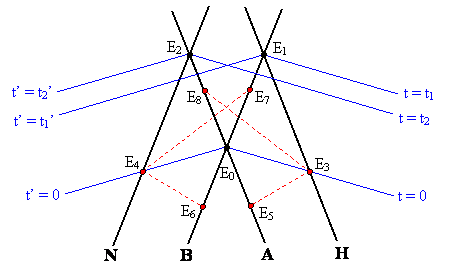
Since Whitehead was Dingle’s source, there is little wonder that Dingle acquired a confused understanding of what the word “event” means in the theory of relativity, and that he conflated relativity and relationism. It’s also easy to see why so many of the scientists who were approached by Dingle with his challenge to defend relativity simply declined. He was obviously so profoundly confused that it would take a huge effort to even re-educate him to the point where he could hope to understand the fallacy of his words. Nevertheless, we must press onward, and analyze the (needlessly convoluted) scenario that Dingle has described, making as many allowances as we can for his misunderstandings of the meanings of the terms he used. Fortunately, the basic physical situation he described is unambiguous, so there is no doubt about what happens at each time and place (modulo the ambiguity in the distances between the clocks, which Dingle left unspecified). A plot of time versus position for the four clocks in Dingle’s scenario is shown below.

The solid black lines show the positions of clocks N and B moving to the right, and the positions of clocks A and H moving to the left. Adhering as closely as possible to Dingle’s nomenclature, we have designated the event at which A and B meet as E₀, and at which B and H meet as E₁, and at which A and N meet as E₂. It must be borne in mind, however, that Dingle conceived of the “event E₀” as not just the time and place where A and B meet, but the entire configuration of the four clocks “when” A and B meet. As we will see, led him shortly into making statements that are complete non sequiturs.

We have illustrated Dingle’s proposed synchronization procedure by the red dashed lines in the figure above, showing the time versus position of a pulse of light emitted from clock A at event E₅, reflected from H at event E₃, and received back at A at event E₈. The event E₀ is mid-way between E₅ and E₈, so the time on clock A at event E₀ is the average of the times at events E₅ and E₈. Therefore, according to this synchronization procedure (specified by Dingle), the reading on clock H at event E₃ is set equal to the reading of clock A at event E₀. Likewise the reading of clock N at E₄ equals the reading of clock B at E₀. The blue lines on the above figure indicate the loci of constant t and constant t’ arising from these synchronization procedures. These show, for example, that clock H at event E₃ reads the same as clock A at event E₀.

We’re now in a position to evaluate Dingle’s alleged contradiction. First he notes (correctly) the following relations, which are direct consequences of the Lorentz transformation between the two relatively moving systems of coordinates:

With this in hand, Dingle at last announces the great contradiction. He says

Between events E₀ and E₁, A advanced by t₁ and B by t₁’ = a t₁. Therefore

But… between E₀ and E₂, B advances by t₂’ and A by t₂ = a t₂’. Therefore

Equations (3) and (4) are contradictory; hence the theory requiring them must be false. Einstein, in his paper, gave only (3), and accepted it as giving the unique value of the rate ratio: he did not check the result by considering the interval between E₀ and E₂. Had he done so he would undoubtedly have seen that his conclusion was erroneous.

The fallacy of this “reasoning” is obvious from a simple inspection of the diagram above, which shows exactly what each of the four clocks reads at every point, all entirely consistent with special relativity and the Lorentz transformation. When Dingle says clock A advances by t₁ between events E₀ and E₁, he neglects the fact that clock A does not move from E₀ to E₁, it moves from E₀ to E₂. Likewise when Dingle says clock B advances by t₂’ between events E₀ and E₂, he neglects the fact that clock B does not move from E₀ to E₂, it moves from E₀ to E₁. Hence his assertions are not just wrong, they are nonsense.

Of course, we can see the trap into which Dingle has fallen. He conceives of the “event” E₀ as entailing not just one specific time and place, but an entire extended configuration of all four clocks, presumably at the “instant” when A and B meet – just as the jealous maiden in Dingle’s 1922 essay perceived the entire configuration of the man and her rival as an “event”. This is clear from the justification that Dingle offers for why “A must be held to read t₁ at E₁ (even though, according to special relativity, A is never at E₁!). His justification for this crucial point is that “H reads t₁ at this event, and on this theory the process by which A is set in relation to H synchronizes it with H.” This statement is true, but Dingle’s conclusion obviously does not follow from it. In fact, as can be seen by a glance at the above diagram, the synchronization of A and H ensures that Dingle’s conclusion (even making allowances for his mistaken concept of “event”) is false. Like every anti-relativityist, Dingle has failed to account for the relativity of simultaneity for coordinate systems related by the Lorentz transformation, and has simply tried to apply the time dilation formula by itself, neglecting the offsets corresponding to differences in spatial positions. Thus he has not applied special relativity at all, so when he says the theory requiring (3) and (4) must be false, he is referring not to special relativity, but to a collection of his own misunderstandings… which are indeed logically self-contradictory.

We should also mention that Dingle’s specification of the “sequence” of events was fallacious. As can be seen from the above diagram, event E₁ precedes event E₂ in terms of the rest frame coordinates of clocks B,N, but the sequence of these events is reversed in terms of the rest frame coordinates of A,H. This just shows (again) how fundamentally inconsistent were the conceptions employed by Dingle compared with those of special relativity, despite the fact that he claimed to be strictly applying only the conceptions of special relativity.

Setting aside the obvious logic errors in Dingle’s technical argument, it’s clear that his underlying motivation was philosophical, arising from his confusion as to the nature of special relativity. At the very beginning of his 1940 monograph he wrote

The principle of relativity may be stated thus: There is no meaning in absolute motion…  If the reader imagines himself alone in empty space, with no landmark, winds, or any other external reference mark to tell him that he is moving, he will probably feel no difficulty in assenting to the proposition that it is immaterial whether he considers himself to be at rest or moving in any arbitrary manner… The principle of relativity is purely negative in character: it asserts merely that ‘absolute motion’ is a meaningless succession of characters…

We can see from this, and many other similar statements, that Dingle had always mistaken relativity for a relational theory, perhaps misled by the similarity of the words. He certainly is not the only person to have made this mistake, but it is quite clear that he firmly believed the theory of special relativity was based on the Leibnizian principle of relationism. In fact, his 1940 book even contains some of the same relationist assertions that Leibniz made in his famous debate with Samuel Clarke. For example, Dingle asserts that

…if we suppose the whole universe to be suddenly moved with any speed in any direction, then, provided that all the relative motions within it are unchanged, no one could know of the fact.

Thus Dingle fundamentally confused the principles of relativity and relationism, which are actually at opposite ends of the historical debate between absolute and relational theories of motion. The special theory of relativity, no less than Newtonian mechanics, is a purely absolutist theory, because just like its predecessor it gives a distinguished role to inertial coordinate systems and inertial motion, and (despite Mach’s hopes) inertia is not defined in terms of the relations to other bodies. According to pure relationism, inertia has no meaning, which is why Clarke/Newton responded to Leibniz with the famous example of the spinning pail, proving that an empirically viable mechanics cannot be based (at least not in any straightforward way) purely on the spatial relations between bodies. This is why both Newtonian physics and the special theory of relativity are firmly based on the principle of inertia, not on the principle of relationism.

This clearly explains Dingle’s predicament regarding the twin paradox. If it were not for the asymmetry in the kinematic relations between the twins and all the other objects in the universe (which Dingle never considered), he would have been correct in his belief that, for a purely relational theory, in a universe with no absolute inertia, we would have no basis for predicting asymmetric aging of the twins. But this observation merely shows the weakness of relational theories of motion, and is irrelevant to special relativity. Dingle never seems to have questioned his life-long belief that special relativity was a relational theory. Apparently the word “relativity” was so similar to “relationism” that he simply took it for granted that they were the same thing, when in fact they are nearly opposites. He never grasped the fact that special relativity is not (and never was) a relational theory. This explains his incessant charge that special relativity contradicted its own principles. What he meant was, special relativity does not adhere to the principle of relationism, but of course relationism is not among the principles of special relativity. Now, if Dingle had been a more competent thinker, he might have argued (like Leibniz) that our theories ought to be relational, and that we ought to seek the origin of inertia. However, as mentioned previously, Dingle made a point of dismissing any consideration of such issues. He really seems to have been clueless.

As an aside, just to give an example of the quality of Dingle’s scholarship, he was fond of informing people that the notion of two distinct quantities which could be called inertial mass and gravitational mass “is found nowhere in Newton’s Principia”. He even wrote a paper explaining this to his colleagues. And yet, on the very first page of the Principia, after defining mass as the product of density and volume (which he presently related to a body’s resistance to acceleration), Newton says

It [mass] can also be known from a body's weight, for - by making very accurate experiments with pendulums - I have found it to be proportional to the weight...

So Dingle’s thesis (as a historian and philosopher of science) was that Newton never recognized that the two quantities, i.e., weight and resistance to acceleration, were distinct and proportional to each other, despite the fact that Newton specifically says precisely this on the very first page of the Principia.

It’s tempting to attribute some of Dingle’s scholarly attributes to his unusual schooling. He actually left school at the age of 14, and worked as a clerk for 11 years, until, during the first world war, he got a scholarship to attend college. As a Quaker he was exempt from military duty. I don’t know if there was any connection between the start of conscription in Britain at that time and Dingle’s entering college. In any case, he was 25 years old, when he began his first formal schooling since leaving high school at 14. He studied astronomy in school, but ended up making his life’s work in the history and philosophy of science, a field in which he was self-taught. His chief qualification seems to have been his contentiousness and doggedness in promoting his own views.

The reader may wonder why no one explained Dingle’s errors to him during these years. In fact, they were explained to him in excruciating detail, and many time over. As can be gathered from the above discussion, Dingle was profoundly wrong in so many ways and on so many different levels, that it was easy (perhaps too easy) for people to issue corrections. Among those who did so was W. McCrea, whose careful explanation of several of Dingle’s misconceptions was printed along with Dingle’s letter to Nature in 1967. McCrea wrote (perhaps naively)

It may help if I enumerate a sequence of arguments; the first alone is sufficient to refute Dingle's contention, but I hope the rest throw further light on the subject as a whole.

His explanations didn’t affect Dingle in the least. In latter issues, additional respondents provided explanations, intended to help Dingle (and others) see clearly the fallacy of his arguments. For example, in one 1973 issue of Nature alone there appeared explanatory letters from H. L. Armstrong, F. H. Fremlin, R. Jacob, M. Whippman, and G. E. Stedman. Did Dingle carefully consider all of these answers and explanations that he had so earnestly solicited, and re-examine the validity of his views? He replied as follows:

It would be profitless to deal separately with the latest "answers" to my question; their diversity tells its own tale, and the writers may see their misjudgments corrected in my book. I have through the years put the question in various forms to meet successive obscurations, but in vain. Though wholly understandable to any ordinary layman it is at once submerged in such mathematical and metaphysical mysticism that normal readers either conclude that its simplicity must be deceptive and I deluded, or express to me their astonishment at the denseness of the "authorities".

Thus, when given not just one but a multitude of diverse reasons why his views were wrong, Dingle interpreted the very multiplicity of those reasons as evidence that the reasons must be “misjudgments” that he could safely disregard. At about this same time the Royal Astronomical Society chose to no longer facilitate Dingle’s activities, and he began sending letters to Nature demanding in terms of outrage that they publicly chastise the Society for its disgraceful behavior. The editors of Nature replied that it was not their charter to police the activities of the RAS. And so it went until Dingle’s death in 1978 at the age of 88.

One last point deserves mention. Dingle says that Einstein never noticed that the time dilation between relatively moving systems of coordinates is reciprocal, and that if he had noticed this, Dingle is sure Einstein would have realized the error of his ways. It is almost inconceivable the Dingle could imagine such a thing. The reciprocity of both length contraction and time dilation between relatively moving systems of inertial coordinates was the very first thing that everyone noticed about the Lorentz transformations, including Lorentz, Poincare, Einstein, Minkowski, and every other person who has ever examined the Lorentz transformations for more than 5 seconds. The resolution of the apparent incompatibility of the relativity principle and the light-speed principle, which was Einstein’s great insight in 1905, was precisely the recognition that this reciprocity is not logically inconsistent if we account for the relativity of simultaneity between relatively moving systems of inertial coordinates. No aspect of special relativity (or of any physical theory) has ever received more critical attention than the reciprocity of space-time relations under Lorentz transformations. In view of this, it seems beyond belief that Dingle, a student of the history and philosophy of science for over fifty years, could blithely claim that this reciprocity had escaped Einstein’s (and everyone else’s) attention. It’s hard to avoid the conclusion that, at this stage, Dingle was simply not in his right mind.

Return to MathPages Main Menu