|
Acute Problem |
|
|
|
PROPOSITION: There do not exist four distinct points A,B,C,D on the plane such that the interior angles of the triangles ABC, ABD, ACD, and BCD are all acute. |
|
|
|
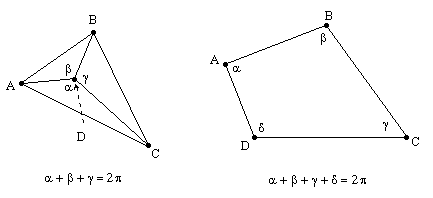
PROOF 1: If one of the four points is inside the triangle formed by the other three, then the angles of the three triangles meeting at that point sum to 2π, so they cannot each be acute (i.e., less than π/2). If none of the four points is inside the triangle formed by the other three, then we have a convex quadrilateral ABCD, and the four interior angles ABC, BCD, CDA, and DAB sum to 2π, so they cannot each be acute. |
|
|
|
|
|
|
|
PROOF 2: Given any two points A and B on the plane, construct the lines Lab and Lba perpendicular to the segment AB through the points A and B respectively. Also, construct the circle on the diameter AB. The triangle formed by A, B, and a third point C will have all acute interior angle if and only if C falls between Lab and Lba and outside the circle on the diameter AB. |
|
|
|
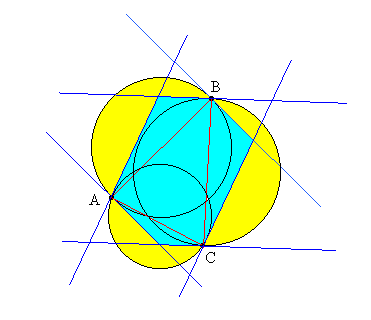
Assuming such a point C has been selected, we can now construct the lines Lca, Lcb, and Lbc. Since ACB forms an acute interior angle, it follows that the lines Lac and Lbc must intersect inside the circle with diameter AB (because their interior angle must be obtuse). Similarly, the intersection of Lca and Lba is inside the circle with diameter BC, and the intersection of Lab and Lcb is inside the circle with diameter AC. These six lines form a convex hexagonal region, and any fourth point would have to fall inside this hexagon to make all the angles acute. |
|
|
|
However, each of the vertices of this hexagon is on or inside the three overlapping circles with diameters AB, AC, and BC, and the fourth point would have to fall outside all of these circles. Therefore, if the circle completely cover the hexagon, there is no place that a fourth point could be located such that all the conditions of the problem are satisfied. |
|
|
|
|
|
|
|
To prove that the three circles with diameters AB, AC, and BC do in fact cover the entire region inside the hexagon, note that the isosceles right triangles with the hypotenuses AB, BC, and CA necessarily overlap because the angles ABC, BCA, and CAB are all acute and therefore less than the sum of two 45 degree angles (and the three circles certainly cover those right triangles). Also, the hexagon cannot extend outside the circles, because (for example) the angle between the line perpendicular to BC (at C) and the line perpendicular to BA (at A) equals the angle ABC, which is acute, so the complementary angles are obtuse, from which it follows that the vertex of the exterior triangle on AC is inside the right triangle, and therefore inside the circle on AC. |
|
|