A Complex Domain for Probability

Given two independent events X,Y with probabilities x,y (relative to some sample space S), let x' and y' denote the probabilities of {X U Y} and {X ∩ Y} respectively. These values are given by the simple formulas

This is based on the usual definition of the probability of an event X relative to a sample space S as

so the probability of the empty set is 0, and the probability of the entire sample space is 1. Clearly all probabilities (according to this definition) are real numbers on the interval 0,1. We could, however, choose a different parameterization. For example, we could assign the empty set a "probability" of –1 and the complete sample space a "probability" of +1.

To understand why we might want to make such an unusual definition, consider the typical association of the probabilities 0 and 1 with the logical operators Falsity and Truth. Letting F(x) and T(x) denote the Falsity and Truth, respectively, of an event x, we have the identities

Obviously these operators act just like +1 and –1 under ordinary multiplication, where we have

Thus, by mapping the operators Truth and Falsity to the numerical values +1 and –1, both of the operations are represented by ordinary multiplication. In contrast, with the usual associations False = 0 and True = 1, the simplest algebraic analogs are

Of course, this f(x) still has period 2, and we could generalize to other "existential operators" by assigning a linear fractional transformation to each one, such as g(x) = 1 – 1/x (which has period 3), or h(x) = (1+x)/(1–x) (which has period 4). However, these Mobius transformations are really just rotations of the Riemann sphere, and the simplest expression of such rotations is just pure multiplication of (in general) complex numbers. In this sense, it could be argued that the associations {False = –1, True = +1} are more natural.

Another interesting feature of the {–1,+1} mapping is the fact that it gives formally symmetrical probability equations for the union and intersection of independent events. The "probability" u of X in the {–1,+1} framework is related to the corresponding old-style probability x by u = 2x – 1. In terms of the example cited earlier, if we set u = 2x – 1, v = 2y – 1, u′ = 2x′ – 1, and v′ = 2v′ – 1 we find that the equations for the union and intersection are

This formalization highlights the fact that if m is the mid-point between two probabilities u,v, then m is also the midpoint of the union and intersection probabilities u′ and v′. (Of course, this is equally true with the usual 0,1 mapping, but the symmetry between these two operations is less apparent. On the other hand, the logical duality of AND and OR under negation is certainly clear in DeMorgan's Rules.)

Now that we've assigned the Truth and Falsity operators to +1 and –1 respectively, it's natural to ask what sort of existential operator might be assigned to i = . To make it fit into the same scheme, this mysterious operator - let's call it the "Width" W(x) - would have to satisfy the relation

In other words, the Width of the Width of x must equal the Falsity of x. Similarly we could define the Height H(x) to correspond with –i. In this scheme of things the "probabilities" could be complex numbers. It's tempting to think that we could restrict our probabilities to the unit disk in the complex plane, but it turns out that this set of points is not closed under the operations for the union and intersection. This leads to the question of what regions of the complex plane are closed under the independent probability operations. Obviously the real interval (–1,1) is one such region, as so is the entire complex plane, but are there any others?

Interestingly, it turns out that the disk of radius 2 centered on the real number 1 is closed under unions, and the disk of radius 2 centered on –1 is closed under intersections. But what about a region closed under both operations? For this purpose the definition of "closure" may need to be adjusted slightly.

Recall that the midpoint of two events is also the midpoint of their union and intersection. Therefore, given any two points in the complex plane, repeated application of equations (1) yields successive pairs of points that essentially rotate about their fixed midpoint and change their radius. So let the word "closure" signify that repeated applications of (1) to a pair of points centered on a point c results in a sequence of pairs that remain bounded in their distance from c. The set of all these c points could be called the natural domain of complex probability.

Notice that the above notion of closure referred to any two initial points centered around c, but this isn't quite right. The quality of boundedness is fairly insensitive to the choice of points (for points in the neighborhood of c), but to be more precise I should say that c is in the "closure region" iff iteration of equations (1) on the initial pair u = v = c leads

to a bounded sequence.

Letting z denote the "radius" of the points u and v relative to their mid-point c, the repeated application of equations (1) for a given fixed center c gives the iteration

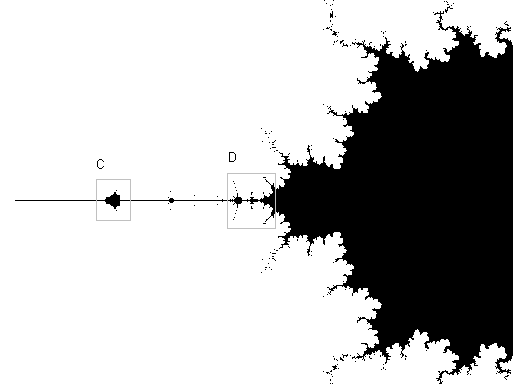
So the natural domain of complex probability may be considered the set of complex points c such that this iteration beginning with z = 0 remains bounded. Since this is just a simple quadratic mapping, it's not surprising that the resulting set of points is a modified version of the familiar Mandelbrot set. However, like everything else associated with the {–1,+1} scheme, the "True" and "False" regions are symmetrical, as shown in the figure

below.

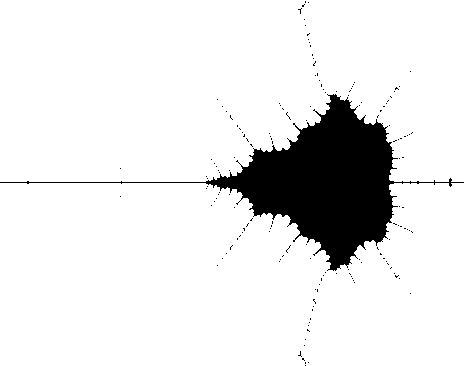
Close-up of Region A:

Close-up of Region B:

Close-up of Region C:

Close-up of Region D:

Return to MathPages Main Menu