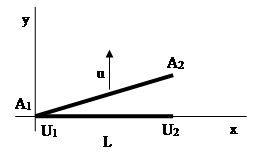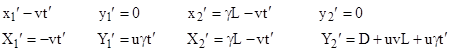A Budget of Barn Poles

The traditional "barn pole paradox" in special relativity begins with the observation that a pole whose rest length is (say) twice as great as the length of the barn could fit entirely within the barn if it was being carried at great enough speed. In this condition both the front and back doors of the barn could be closed, completely enclosing the moving rod. The "paradox" consists of the observation that, with respect to the rest frame of the pole, the barn is contracted to just one fourth the length of the pole, so the pole cannot possibly be fit inside the barn. The resolution of this elementary paradox is, of course, given by taking into account the relativity of simultaneity, as illustrated in the figure below.

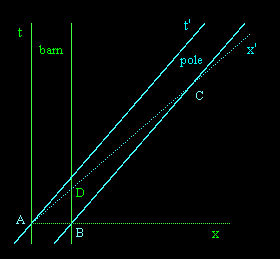
The worldsheet of the barn is described by the two parallel green lines, and the lines designated as x and t are the space and time axes of the barn's inertial rest frame coordinate system. The worldsheet of the pole is indicated by the two parallel blue lines, and the lines designated as x' and t' are the space and time axes of the pole's inertial rest frame coordinate system. The x,t and x',t' system are related by a Lorentz transformation for the speed 0.866c. As shown in this drawing, the spatial extent of the pole at any time slice t = constant with respect to the barn's inertial rest frame coordinates is the segment AB, which is also the barn's spatial extent. Hence the pole just fits inside the barn. However, with respect to the inertial rest frame coordinates of the pole, the barn's spatial extent at any time slice t' = constant is the segment AD, whereas the pole's spatial extent on this time slice is the segment AC. We have the ratio |AD|/|AC| = 1/4, so the pole does not fit entirely within the barn at any instant t' = constant. Of course, this does not conflict with the fact that it does fit entirely within the barn at one particular instant t = constant. Naturally if the back door of the barn is closed when the leading edge of the pole reaches it, the pole will begin to compress, but the effects of this compression cannot propagate backwards faster then the speed of light, so the trailing end of the pole will continue to advance as if nothing had happened until it is inside the barn, at which point the pole will have be at rest (relative to the barn) and compressed to half of its original rest length.

Trivial examples of relativistic kinematics like this are not difficult to devise. Needless to say, the simple Lorentz transformation

cannot possibly lead to logically contradictory relations in terms of the (x',t') coordinates if applied to any logically consistent situation expressed in terms of the (x,t) coordinates. Nevertheless, with the mentality of "angle trisectors", some modern paradoxers persist in endlessly trying to invent scenarios that will somehow (in defiance of simple algebra) produce a contradiction from the Lorentz transformation. All these attempts are essentially just variations on the barn pole paradox. Below we discuss three such variations, one expressed in terms of probabilities, another expressed in terms of electrical currents, and finally one involving the composition of motion in two (or three) spatial dimensions.

For the first "paradox", let (x,t) denote a system of inertial coordinates, and suppose an event E occurs at (X,0) where X is randomly chosen from a uniform distribution on the range 0 to L. Also, suppose a rod R₁ of length p is at rest relative to this coordinate system, and positioned so that the coordinates of its two end points are (0,0) and (p,0). The probability of the event E occurring within the span of R₁ is p/L. Now suppose there is another rod R₂ of rest length p moving with speed v in the positive x direction. If the trailing edge of R₂ is at x = 0 when t = 0, then the leading edge is at x = pγ when t = 0, where γ = (1−v²)^1/2. The probability of the event E occurring within the span of rod R₂ is pγ/L. If we consider the same situation in terms of the inertial coordinate system (x',t') with respect to which R₂ is at rest, we will obviously find the same probabilities for the event E to occur in the spans of R₁ and R₂, because these probabilities are just ratios of fixed segments of the x axis, and are all changed in proportion to each other by any Lorentz transformation. To spell this out explicitly, the locus of possible positions for the event E is the line from (0,0) to (L/γ,−vL/γ), and the intersection of this line with the worldsheet of R₁ is the line from (0,0) to (p/γ,−vp/γ). Thus R₁ covers p/L of the range for event E, and the probability of E occurring in the span of R₁ is p/L. The intersection of the E-locus with the worldsheet of R₂ is the line from (0,0) to (p,−vp), so it covers pγ/L of the range for the event E, and the probability of the event occurring within R₂ is pγ/L.

Incidentally, a naive paradoxer might point out (correctly) that the intersection of the worldsheet of R₂ with the x' axis is of length p, and the intersection of the worldsheet of the spatial range 0 to L (fixed with respect to x,t) with the x' axis has the length γL. On this basis he might argue (incorrectly) that the probability of the event E falling within the span of R₂ should be p/γL, contradicting the fact (shown above) that the probability is pγ/L. Needless to say, the paradoxer's error is failing to account for the fact that the specified range for event E is along the x axis, not along the x' axis.

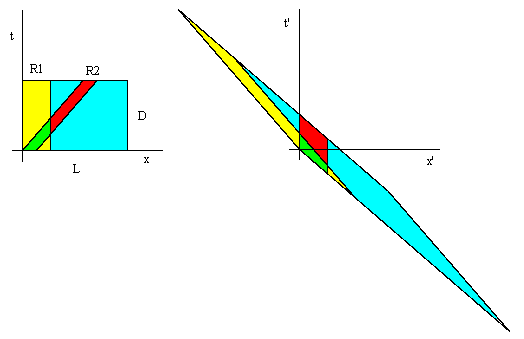
For an interesting variation on this problem, suppose we let not only the location but also the time of occurrence of event E be randomly selected from a uniform distribution over a finite range. In other words, for a system (x,t) of inertial coordinates, suppose an event E occurs at (X,T) where X is randomly chosen from a uniform distribution on the range 0 to L, and T is randomly chosen from a uniform distribution on the range 0 to D. Then, as before, consider the two rods R₁ and R₂ of rest length p, the former stationary with respect to (x,t) and the latter moving in the positive x direction with speed v. In this case the probability of the event E falling within the span of R₁ (or R₂ respectively) is given by the ratios of the spacetime area swept out by R₁ (or R₂) to the total spacetime area of the specified range for event E. When plotted in terms of the (x,t) coordinates, the situation is as shown in the left-hand figure below.

The right-hand figure represents the same situation plotted in terms of the rest frame coordinates (x',t') of R₂. For this problem the consistency of the probabilities is, if anything, even more obvious than in the case of an "instantaneous" event E, because of the fact that spacetime areas are conserved under arbitrary Lorentz transformations of the (x,t) plane. This follows from the invariance of all quantities of the form x₁t₂ – x₂t₁ under Lorentz transformations, together with the elementary expression for areas enclosed with arbitrary plane figures in terms of quantities of this form. (See the note Net Area and Green's Theorem.) The invariance of this form is equivalent to the fact that the determinant of the Lorentz transformation is unity.

The next paradox we will discuss involves a sequence of three light bulbs positioned at uniform intervals along the x axis of an inertial coordinate system (x,t). The bulbs are stationary at the x coordinates 0, 1, and 2. Now consider a rod of rest length equal to 2 units, but moving in the positive x direction with velocity v such that v² = 3/4, which implies that it's length relative to the (x,t) coordinates is just 1 unit. Also, suppose the lights are triggered to turn ON when, and only when, they are in contact with the rod. Thus there is always exactly one light bulb illuminated at any given time t while the rod is passing over the lights. For example, at the time t illustrated below, bulb 0 if OFF, bulb 1 is ON but is about to go OFF as the rod proceeds to the right, and bulb 2 if OFF but will turn ON as soon as the leading edge of the rod reaches it (at which point bulb 1 will go OFF as the trailing edge of the rod passes over it).

Now, just as in the Barn Pole paradox, we are asked to consider the same situation in terms of the rest frame coordinates (x',t') of the rod. The alleged paradox is due to the fact that, in terms of these coordinates, the rod has length 2 units whereas the distance from bulb 0 to bulb 2 is only 1 unit, and hence the rod is in contact with all three bulbs for a period of time, implying that all three bulbs are on simultaneously.

Realizing that these facts are easily reconciled by means of the relativity of simultaneity, the paradoxer tries to achieve a contradiction by asking us to consider the current flowing in a series circuit supplying the three bulbs from a single battery located at bulb 0. He suggests that, from the standpoint of the (x,t) coordinates, the current should just equal one unit for the duration of the time that the rod is interacting with the bulbs, since only one bulb is ON at any given time t. On the other hand (he reasons), from the standpoint of the (x',t') system, the current must reach 3 units for a period of time, because all three bulbs are ON. So, he asks, does the current ever reach 3 units, or doesn't it?

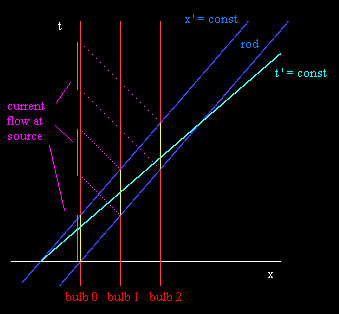
As always (when dealing with such purported paradoxes), a simple spacetime diagram suffices to explain the real situation. The figure below shows the worldlines of the three bulbs in red, with their periods of illumination shown in yellow. The worldlines of the leading and trailing edges of the rod are shown in dark blue, and the axis of simultaneity for the rod's rest frame is shown in light blue (marked as "t' = const”).

For purposes of discussion we have represented each bulb as a source of current when it is turned on, and the battery at bulb 0 is regarded as a sink for the current. We have also assumed the propagation speed c for the current, and we are ignoring transient fluctuations. As can be seen, there are three separate periods of current flow at the "source" (i.e., the battery at bulb 0), each with one unit of current. Also, notice that even though the rod covers only one bulb at a time with respect to this coordinate system, it covers all three bulbs simultaneously with respect to the (x',t') coordinate system.

Transforming this situation to the (x',t') coordinate system gives the situation shown in the figure below.

Naturally there are "instants" (i.e., loci of constant t') in which all three bulbs are ON simultaneously, but of course the current flow at the source still consists of three disjoint periods with one unit of current during each period. Needless to say, it was a foregone conclusion that the sequence of distinct changes in current level along the worldline of bulb 0 (or along any other worldline) would translate into a similar sequence with respect to any other system of inertial coordinates. Straight lines map to straight lines, and the ratios of intervals along lines are preserved by Lorentz transformations. This just illustrates yet again the utter futility of trying to demonstrate that the Lorentz transformation somehow leads to logically inconsistent results.

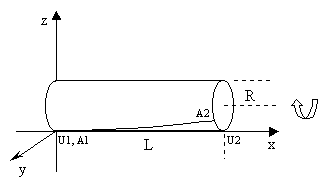
All the examples discussed so far involved just one spatial dimension, but our last example involves motion in two (or three) spatial dimensions. Suppose we have two rods, one stationary rod U₁−U₂ of length L aligned with the x axis, and another rod A₁−A₂ with the same x-extent but "slanted" and moving in the y direction with speed u as shown below:

The ends A₁ and U₁ are coincident at this "instant", whereas the end A₂ was coincident with U₂ some time in the "past". Obviously the rod A₁−A₂ has a greater spatial length than the rod U₁−U₂ in terms of this coordinate system.

Now consider these two rods with respect to a coordinate system whose origin is moving to the right with velocity v. The slices of simultaneity are skewed, so we find (for suitable lengths, speeds, etc.) that with respect to this new coordinate system the event [A₂ coincident with U₂] is simultaneous with the event [A₁ coincident with U₁]. Hence, the two rods have the same spatial length with respect to this coordinate system. Notice that the rod A₁−A₂ is spatially parallel to U₁−U₂ with respect to this coordinate system, whereas the rods are not parallel with respect to the original coordinate system. (This is the same relativistic effect that accounts for both aberration and Thomas precession.)

With respect to the first coordinate system, the spatial coordinates of U₁ are x₁ = 0, y₁ = 0, and the coordinates of U₂ are x₂ = L, y₂ = 0. The coordinates of A₁ are X₁ = 0, Y₁ = ut, and the coordinates of A₂ and X₂ = L, Y₂ = D + ut. Apply the Lorentz transformation to express these positions in terms of a coordinate system moving with speed v in the position x direction. In units such that c = 1, this immediately gives

where again γ = (1−v²)^1/2. Clearly the ends A₁ and U₁ are coincident when t' = 0. We wish to see under what condition the ends A₂ and U₂ are coincident at this same "instant". The x coordinates of the A and U rods are the same (in both systems of coordinates), so we just need to equate y₂' with Y₂'. Noting that t' = 0 at this "instant", this gives 0 = D + uvL, so we have uv = −D/L. Since |v| can be no greater than 1, it follows that |u| must be at least equal to D/L in order for there to exist an inertial reference frame with respect to which the two rods are parallel and of the same spatial length.

This explains how and why two rods in motion with respect to each other can have the same spatial length with respect to one system of inertial coordinates and different spatial lengths with respect to another, just as they can be parallel with respect to one system and not parallel with respect to another. This is an immediate consequence of the relativity of simultaneity, i.e., the fact that two events can be simultaneous with respect to one system of coordinates but not simultaneous with respect to another.

The rest length of the U₁−U₂ rod is simply L, whereas to find the rest length of the A₁−A₂ rod we must transform the coordinates of it's endpoints to the rest frame of the rod, which is moving with speed u in the positive y direction relative to the (x,y,t) coordinates. Therefore, letting γ_u denote the factor (1−u²)^1/2, the rest length of the A₁−A₂ rod is [L² + D²/γ_u²]^1/2. So, if the rods were originally constructed with the same rest length, we see that the A₁−A₂ rod must have been materially stretched in order for it to be in its current state of motion and positions.

In other words, whether or not a rod fractures depends on its rest length, not on its length relative to some moving system of coordinates. In the situation described here the two rods have two different rest lengths, namely, L and L[1 + (D/(Lγ_u))²]^1/2 where D/L = −uv (assuming the rods are parallel with respect to the coordinate system that is moving with speed v in the x direction). So, the ratio of the two rest lengths is [1 + (uv/γ_u)²]^1/2.  Needless to say, if both rods originally had rest length L, then the A₁−A₂ rod has been stretched, and would fracture (if it was sufficiently brittle).

The paradoxer's confusion in this scenario is based on his neglect of the relative motion u between the two rods (since he tends to focus on just the motion in the x direction). In an attempt to impose this confusion on everyone else, the paradoxer sometimes alters the situation so that the rod A₁−A₂ is attached to a cylinder of radius R, whose axis is parallel to the x axis, as illustrated below.

Of course, this doesn't substantially change the situation, because for sufficiently brief intervals of time and small angular offsets, we can simply "unroll" the cylinder (which is an intrinsically flat surface anyway), and reduce this to a two dimensional problem again, letting "y" denote the circumferential position around the surface of the cylinder. Thus we set y = θR and u = ωR where θ is the angular position of the cylinder, ω is the angular velocity, and R is the radius. The spatial length of the cylinder is again just [L² + (D/γ_u)²]^1/2 where D = Rθ and θ is the angular offset of the attachment point A₂ relative to the attachment point A₁ (with respect to the x,y,z,t system).

The only new feature of this rotating version is that the attached rod is not strictly in inertial motion, so it has no single rest frame. To describe it's kinematics in full generality (assuming an ideal kinematic cylinder), we can give its (x,y,z,t) coordinates in terms of a parameter q ranging uniformly from 0 to 1 along its length. We have

so again the spatial length is [L² + D²]^1/2 where D = Rθ and θ is the total angular offset of the two attachment points. In this case we can't transform to the rest frame of the rod, because the rod has no single rest frame, but we can consider each infinitesimal span of the rod and evaluate its length with respect to the momentarily co-moving inertial frame. This is the length that determines the mechanical response for each incremental part of the rod. For each increment the problem reduces to the simple two-dimensional case discussed previously, so the net effect is a total "local rest length" of [L² + (D/γ_u)²]^1/2 for the rod, just as before.

Return to MathPages Main Menu