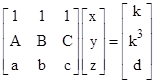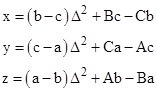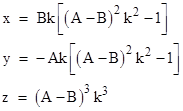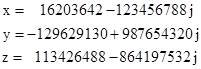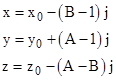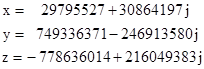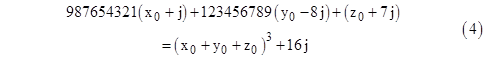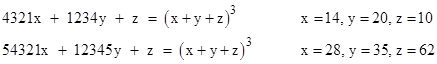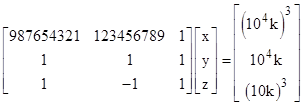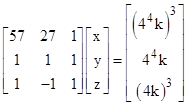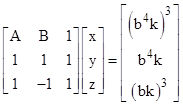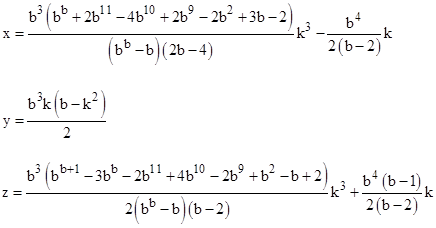A Cubic Puzzle

A puzzle site on the internet asked for a solution, in integers, of the equation

We obviously have the trivial solution x = y = z = 0, but even if we stipulate non-zero integers, it’s easy to give an infinite family of integer solutions of any equation of the form

for constants A, B, C simply by setting k = x + y + z and writing the above equation as Ax + By + Cz = k³.  We can then combine those two linear equations with any other linear relationship ax + by + cz = d for arbitrary parameters a,b,c,d and then solve the system of equations

This gives rational solutions with the common denominator equal to the determinant of the square matrix, i.e.,

To clear the fractions we could multiply k and d by Δ, but for simplicity we can set d=0 and substitute Δ for k to arrive at the triply-infinite family of integer solutions

Of course these are not the only solutions. To explore other families, let’s return to the original form of the equation with C=1, so we have

One primitive approach is to set x = Bw and y = −Aw, in which case the equation reduces to z = s³ where s = x + y + z. Hence we can substitute for z in the above equation, take the cube root of both sides, and re-arrange the terms to give

Now if we set s = (A−B)k for some arbitrary integer k, we can substitute for s and solve for w to give

Consequently for any integer k the cubic (2) is satisfied by the integers x,y,z given by

More generally, any equation of the form (2) can be re-written as

where (again) s = x + y + z. For any chosen value of s (provided it doesn’t violate any divisibility requirements) this equation has infinitely many integer solutions given by the Euclidean algorithm. For example, if we choose s = 1000, the original cubic (1) is

This has the infinite family of solutions

More generally, if x₀, y₀, z₀ is any solution of (2), then so is x₀ + αj, y₀ + βj, z₀ + γj provided that

Therefore, setting α = −(B−1), β = (A−1), γ = −(A−B), we have the infinite family of solutions

Since we can find such an infinite family of solution for any chosen value of s (satisfying the divisibility requirements), we have a doubly-infinite set of integer solutions of (1). Incidentally, one puzzle site asked for a solutions of (1) in integers (positive or negative) with the minimum positive value of s = x+y+z. Several solutions for small values of s (e.g., 49, 20, 13, …) were posted over a period of several years, apparently the result of brute force searching on computers. After five years of this, someone posted a solution with x+y+z = 1, which of course is trivial to find using the Euclidean algorithm as described above. Moreover, we can see by inspection with s=1 that a solution of the general equation (2) is given by x = (B−1)/4, y = (1−A)/4, z = 1 + (A−B)/4, so we have an infinite family of solutions with s=1.

The preceding solutions don’t require the x and y terms to cancel out, but they typically lead to solutions in which either x or y is negative. By a suitable choice of s we can find solutions with x and y both positive, but then we typically find that the value of z is negative. For example, with s = 495884 the Euclidean algorithm gives the solutions

Another simple approach to generating solutions of (1) is to note that if the integers x₀, y₀, z₀ are a solution then

for any integer j. Consequently, if X, Y, Z are any integers such that (1) is satisfied modulo 16, then the value of j is given by

and from this we can compute the solution

All these methods give solutions that satisfy the original stated puzzle, which asked for integer solutions, but it isn’t obvious that any of these methods gives solutions in strictly positive integers.

It is certainly possible to have positive integer solutions to some equations of the form (2). For example, the equation

has the solution x=1, y=2, x=1. Also, the equation

has the solution x=13, y=7, z=8. More in the spirit of the original puzzle, we also have

We also have two solutions for

As an aside, we note that there is also a solution of the “54321” equation with z = 0, so we have a solution of the two-variable relation

In general a two-variable equation of the form

is more tractable, because the left side can be written as A(x+y) − (A−B)y, which implies that x+y must be a divisor of A−B (assuming x and y are co-prime). Therefore, letting s denote x+y and putting this equal to each divisor of A−B, we can compute rational values of x and y by solving the two equations Ax + By = s³ and x + y = s. This gives

In order to make x and y positive, the value of s² must be between A and B, so we need only check the divisors of A−B that are between √A and √B. This enables us to determine very efficiently all the positive integer solutions (if any) of (5) for any given values and A and B. For example, by this method we can prove that there are no positive integer solutions of

On the other hand, for the equation

we have A – B = (2²)(6736)(32069), and if we set s = (2²)(6736) we get the positive integer solution x = 18795, y = 8153.

Returning to the original three-variable equation, we can adapt the same approach, assuming s and z are given, and computing the values

We know there are no positive integer solutions x,y with z=0, but we can check other positive values of z for each value of s. In this case it is not necessary for s to be a divisor of A – B, but we can still check the values of s in a suitable range. For x and y to also be positive, the value of s must be between roughly √B and √A, although the exact range needs to be somewhat greater to account for the positive z. It’s sufficient to check s values from about 9000 up to about 32000.  By this method we find that equation (1) has the positive integer solution x = 27150, y = 1500, z = 1350. A second solution in positive integers is x = 7350, y = 6000, z = 6650, and a third solution is x = 450, y = 4500, z = 5050. Interestingly, taking these solutions in reverse order, the quantity x + y + z equals 10⁴k and the quantity x – y + z equals (10k)³ for k=1,2,3. Thus we have

Solving this for x,y,z, we get

Substituting these expressions back into (1), we find that they do indeed satisfy the equation identically, although the values are all positive only for k = 1, 2, and 3.

This is an example of a generic identity that applies to any base. For example, working in the base b=4 we can use the coefficients A=321₄ and B=123₄, which have the decimal values 57 and 27 respectively. Inserting these into the above matrix equation gives

which has the solution

This clearly doesn’t give any solutions with all positive integer values. In general for any base b the coefficients A and B given by the non-zero digits in decreasing or increasing order (respectively) are

and with these values the solutions of

are given by

These represent rational, but usually not integer, solutions of (1). The bases 4 and 10 are unusual in the sense that the algebraic expressions for x,y,z are all integers. Note the special algebraic factorizations and cancellations that occur when the exponent b equals 4 or 10.

The case b=100 is numerologically interesting, since the numerators and denominators of the coefficients of k³ in the expressions for x and z consist of long strings of repeating complementary pairs of digits.

Return to MathPages Main Menu