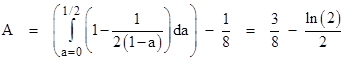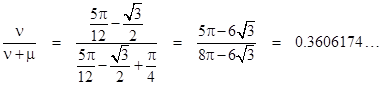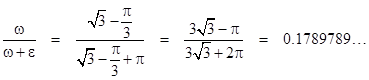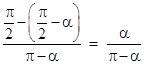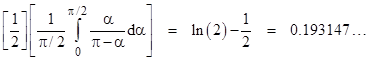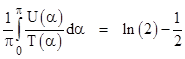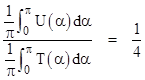Probability of a Random Triangle Being Acute

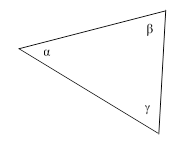
What is the probability that a randomly defined triangle will be acute (i.e., each of the interior angles are less than a right angle)? The question is under-specified, because the distribution of triangles is ambiguous. We can imagine several different ways of constructing a triangle “at random”, and arrive at different answers. For example, since our interest is purely in the shape of the triangle, regardless of size, we might randomly select the three interior angles, which we may denote as α, β, and γ as depicted below.

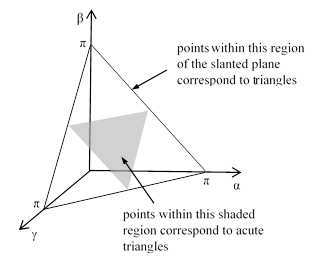
Obviously we have the constraint α + β + γ = π. Also, for a general triangle, each angle must be in the range 0 to π, and for an acute triangle each angle must be in the range 0 to π/2. The regions of the α,β,γ configuration space satisfying these constraints are shown below.

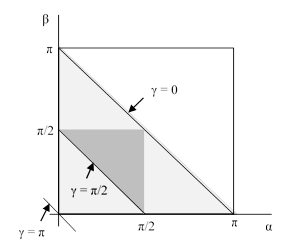
Assuming the probability density for the triangle configuration points is uniformly distributed in this space, we see that the acute triangles comprise 1/4 of all triangles. This can also be depicted by projecting the α, β, γ space onto the α,β plane as shown below.

Here the combined shaded regions represent all possible triangles, and the darkly shaded region represents the acute triangles. We note that the projection preserves the ratios of areas. Again, if the probability is uniformly distributed throughout the combined region, it follows that the probability of a randomly selected triangle being acute is exactly 1/4.

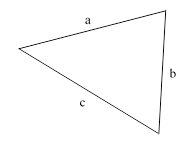
However, there are other plausible ways of “randomly” selecting a triangle, leading to different distributions and different probabilities of being acute. For example, consider a general triangle with edge lengths a, b, and c as depicted below.

Since we are interested only in the shape of the triangle, not in the size, we can normalize the edge lengths of any triangle so that a + b + c = 1. Projecting this plane surface onto the a,b plane, we note that the region satisfying the triangle inequalities

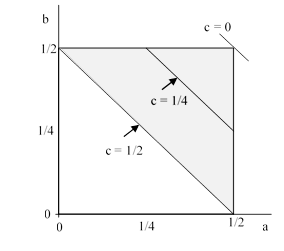
is the upper-right half of the square shown below.

The diagonal boundary line of the shaded area satisfies a + b = 1/2 with c = 1/2, the top boundary satisfies a + c = 1/2 with b = 1/2, and the right hand boundary satisfies b + c = 1/2 with a = 1/2. Every possible normalized triangle corresponds to a point in the shaded area. The acute triangles are those that satisfy the more restrictive conditions

Using the normalizing condition c = 1 – a – b, we can eliminate c from these relations, and we can express the boundaries of the region of acute triangles by

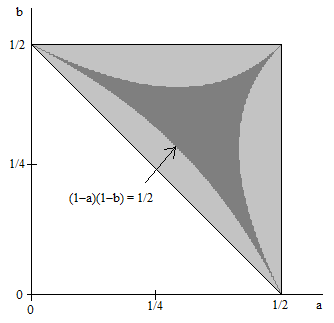
These three boundary curves are shown in the figure below, outlining the region of acute triangles (the darkly shaded area) within the region of all possible triangles.

The area below the main diagonal is 1/8, so the area of the lightly-shaded region bounded by the main diagonal and the curve (1−a)(1−b) = 1/2 is given by

The other two lightly-shaded regions have the same area as this, because of the symmetry in the full a,b,c space, and because the proportions are maintained under linear projection. (In the full a,b,c space the boundaries are the intersection of the diagonal plane with right cones from the origin on the three axes.) Therefore, subtracting these three areas from the area of the combined shaded region (i.e., 1/8), we find that the darkly shaded region (corresponding to the acute triangles) is (3/2)ln(2) – 1. Assuming the probability is uniformly distributed in this space, we get the probability that a randomly selected triangle is acute by dividing this area by the combined shaded area 1/8, which gives

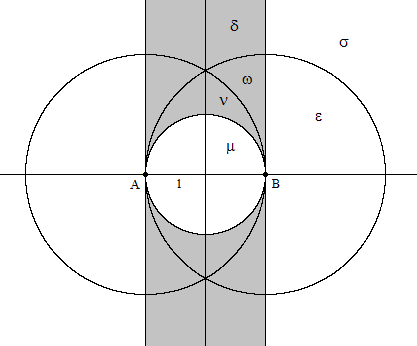
Still another approach to the original question is to consider choosing three points arbitrarily on the plane, and then determine what fraction of them form an acute triangle. Incidentally, Charles Dodgson posed the question in this form in his 1893 book of mathematical puzzles, entitled “Pillow Problems Thought Out During Wakeful Hours”. His Problem 58 posits “three points taken at random on an infinite plane”, and asks for the probability that they are the vertices of an acute triangle. (Actually he asked about obtuse triangles, which is obviously just the complement.) However, as plausible as this question might sound, the premise of choosing three points "randomly" in the plane is not valid – at least not without giving a probability distribution for the points. There is no uniform distribution over the plane, so the notion of choosing three points randomly on the plane is inherently ambiguous. Oddly enough, Dodgson apparently didn’t notice this ambiguity. His solution was to claim that, given three “arbitrary” points A, B, C in the plane, we can without loss of generality assume AB is the longest side, which constrains the region that must contain C, and then determine what fraction of that region would make the triangle acute. Pictorially, the situation is as shown below.

The triangle ABC will be acute just if point C lies in the shaded region. The figure has four-way symmetry, so we will just focus on the upper-right quadrant. It is straightforward to show that the areas of the marked regions are

and the areas  of δ and σ are both infinite. Now, Dodgson argues that we can assume AB is the longest edge, so point C must lie within one of the regions with the areas marked μ or ν, and the triangle is acute only if C lies in the area marked ν. Therefore, assuming the distribution of C is uniformly distributed in the indicated regions, Dodgson argues that the probability of the triangle being acute is

However, Dodgson evidently overlooked the fact that we could just as well stipulate that AB is the second longest leg of the triangle, in which case the point C must lie in one of the areas marked as ω or ε, and the triangle is acute only if C lies in the area marked ω. On this basis we would say the probability of the triangle being acute is only

There is also a third possibility, which is to choose point C such that AB is the shortest leg of the triangle, in which case C must lie in one of the regions marked d or s, and the triangle is acute only if C lies in the region marked d. Hence we could say the probability of the triangle being acute is δ/(δ+σ), which is zero, since δ is an infinitely small fraction of σ.

These results show that Dodgson’s approach is unsatisfactory, since it leads to different answers depending on whether we assume AB is the shortest, middle, or longest leg of the triangle. The fallacy is related to the fact that, in each of the three alternatives, the location of point C is assumed to be constrained by the positions of A and B, whereas the problem implies the points are chosen independently. To be consistent with the problem statement we could fix the points A and B, but then C must be chosen from a uniform distribution over the entire plane, which, as mentioned above, is not a well-defined proposition.

Incidentally, one internet web site presents an amusingly fallacious “solution”, arguing as follows:  To select a random triangle with interior angles α, β, γ, we can first select α uniformly from the range 0 to π, and then select β uniformly from the range 0 to π – α, and then we have γ = π − α − β. Now, the triangle is acute just if α, β, and γ are each less than π/2, which will occur just if α is in the range 0 to π/2 and β is in the range π/2 – α to π/2. (The lower limit on β comes from the requirement that γ must be less than π/2, noting that γ = π – α – β.) The web site argues that the probability of α being acute is therefore 1/2, and the probability that β and γ are acute is the average of the ratio

for values of α in the range from 0 to π/2. Thus (according to the web site), the probability of a random triangle being acute is the product of these two factors, so we have

In broad outline this approach seems to closely resemble the angle-based solution presented at the beginning of this article, and yet that solution yields the probability 0.25, whereas the web “solution” yields the probability 0.193...  What has gone wrong?  Interestingly, the web site reports that a Monte Carlo simulation was written, carrying out the stated triangle construction recipe, and it confirmed the web site’s answer, which they interpreted as proof that their analysis must be correct. This is a nice illustration of how simulations can confirm a fallacious analytical result, because the simulation simply implements the fallacious analytical reasoning. It’s interesting to examine the error in detail.

Formally, the probability we seek is given by a measure of the acute space divided by a measure of the overall triangle space. For any given α, let T(α) denote the extent of the overall triangle space, and let U(α) denote the extent of the acute space. In agreement with the web site, we have

In these terms, the web site argues that the overall probability is the average of U(α)/T(α) for values of a between 0 and α. Sure enough, this gives

(Notice that, since U(α) = 0 for α > π/2, the upper limit of integration is equivalent to the web site’s formulation.) However, to carry out the reasoning correctly, the probability we seek is not equal to the average of the ratios, it is equal to the ratio of the averages. Thus the correct expression for the probability (based on the assumption of a uniform distribution over the space of interior angles), equal to the acute region divided by the total triangle region, is

Conceptually, the problem with the web site’s reasoning is that it misrepresents the sample space by assuming that each value of α has the same “weight” (i.e., represents the same “number” of triangles). It fails to account for the fact that values of α near π correspond to fewer triangles than values near the middle of the range. To correctly simulate the distribution that the web site clearly had in mind, we would independently select values of α and β uniformly from the range 0 to π, and then discard the cases for which γ (i.e., π – α – β) is not in that range. The overall sample space of triangles consists of just those triples that constitute a valid triangle (noting that this does not include all cases when just α is in the valid range), and the probability we seek is just the fraction of those triangles that are acute. If the web site had simulated this process, they would have gotten the result 0.25. Instead, their simulation simply implemented the same fallacious reasoning that formed the basis of their analytical solution, so it gave the same (erroneous) result – or rather, it gave the probability of producing an acute triangle by the stated method, but that method does not represent a “reasonable choice” as the definition of a random triangle.

Of course, the concept of a "reasonable choice" is itself problematical. We’ve seen that distributions based on uniformity of the angle space or uniformity of the edge-length space lead to different results. Also, the Dodgson solution and the web site’s solution show how easily one can be misled into tacitly adopting unjustified and eccentric distributions without realizing it. (To be fair, the Dodgson treated the problem as an exercise in plane geometry – a favorite subject of his, and the calculus web site treated the problem as an exercise in integration; neither of them gave much thought to whether their formulations accurately represented the probabilistic aspect of the question.) In general, probability problems often implicitly assume some "reasonable choice" for the governing distribution, even though the choice may actually be ambiguous. One might think that we could somehow take the average of all possible choices that satisfy the problem statement, but unless the boundaries of reasonableness are defined in advance, and a distribution (weighting) for the choices is specified, this sort of reasoning is questionable. Ironically, the point of rigorous probability problems is to account for the ambiguous possibilities, no matter how remote, and yet people sometimes argue that we ought to disregard some regions of the space of possibilities. The "improbability" or "unreasonableness" of certain remote cases is precisely what probability theory is intended to quantify, so it would be misguided to gloss over such ambiguities in the statements of problems.

Return to MathPages Main Menu