Solving Magic Squares
What's the most efficient way of generating all possible NxN magic
squares? Obviously trying all (N^2)! possible arrangements and
checking for "magicness" would be prohibitive. Presumably this was
not the method used by Bernard Frenicle de Bessy back in 1693 to
determine that there are exactly 880 distinct 4x4 magic squares, not
counting rotations and reflections. (Does anyone know what method he
actually used?)
There are several more modern treatments of the subject, such as in
the book "Winning Ways" by Conway, but they mainly seem to approach
the question in terms of equivalence classes and transformations of
various kinds. This approach is certainly illuminating, but it's
also interesting to try just "solving" the problem algebraically.
In general, when dealing with NxN squares, where N is odd, it's
helpful to subtract (N^2 + 1)/2 from each of the numbers 1 through
N^2, since this makes all the common sums zero. For example, with a
typical 3x3 square we subtract 5 from each number to give
a b c 1 -4 3
d e f = 2 0 -2
g h i -3 4 -1
which makes it immediately obvious that there is only one possible
magic square of order 3, up to rotations and reflections. This can
also be seen by combining the algebraic conditions on the variables
to eliminate all but two of the variables and arrive at the conic
2a^2 + 2ab + b^2 = 10 (1)
(See Note 1 for derivation.) This is an ellipse with the eight
lattice points
(-3, 2) (-3, 4) (-1, 4) ( 1, 2)
( 3,-2) ( 3,-4) ( 1,-4) (-1,-2)
each of which represents one of the eight rotations or reflections of
a 3x3 magic square. Therefore, equation (1) and the eight lattice
points can be regarded as the "solution" of 3x3 magic squares.
To explicitly solve for these lattice points, note that equation
(1) was based on the linear conditions along with the sum of squares,
and we can derive similar equations based on the sum of cubes, the
sum of 4th powers, and so on. It turns out that the sum of cubes just
gives equation (1) again, but the sum of 4th powers gives the quartic
6 a^4 + 12 a^3 b + 10 a^2 b^2 + 4 a b^3 + b^4
+ 96(2a^2 + 2ab + b^2) = 1078
Substituting for the quantity in parentheses from equation (1),
this reduces to
6 a^4 + 12 a^3 b + 10 a^2 b^2 + 4 a b^3 + b^4 = 118 (2)
The loci of points (a,b) that satisfy equations 1 and 2 are shown
in the figure below:
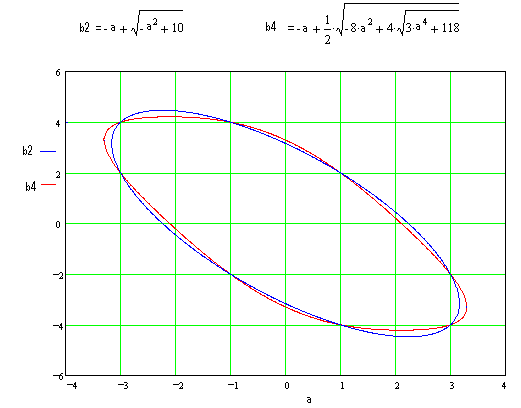 These two ovals intersect at the lattice points. The quartic (2)
happens to have a nice solution in radicals, and the four roots
are all similar to the one appearing in the figure above, with
various signs. We can eliminate b from equations (1) and (2) by
solving each of them for b and setting the results equal. Then
with a little manipulation we arrive at the condition
a^4 - 10a^2 + 9 = (a^2 - 1)(a^2 - 9) = 0
which shows that the value of "a" (which appears in a corner of the
3x3 magic square) must be +-1 or +-3, and those are indeed the four
corner values for the 3x3 magic square, and all the remaining entries
are linearly related to these. Thus we have completely solved for
the entries of a 3x3 magic square. Of course, there is essentially
only one such square, so our solution is unique (up to rotations and
reflections).
For a less trivial case, consider the general 4x4 magic square
a b c d
e f g h
i j k l
m n o p
For even-order squares the quantity (N^2+1)/2 is a half-integer, so
in these cases we convert the original term x' in the range 1-16 to
the corresponding centralized term x in the range -(N^2-1) to +(N^2-1)
by applying the transformation x = 2x'-(N^2+1). Thus, with 4x4 magic
squares, instead of working with the values 1 through 16 we work with
signed odd integers -15,-13,..., +15.
Making use of the algebraic conditions on these 16 variables, we find
that a square can often be determined by the values assigned to just
5 elements (but see below for exceptions). This is because, given the
centralized values of g, h, k, l, and p, the values of f and o must
satisfy the equation
(f+A)(Bo+C) = DE (2)
where
A = 2p+k+l+h B = g+k D = A-g C = E+F
E = (l+k)(l+h) + p(g+h+l+k) F = (k+p)(k+g) + k(l+h)
To illustrate, consider the square in Albrecht Durer's engraving
"Melencolia", which has
g'=11 h'=8 k'=7 l'=12 p'=1
or, in centralized terms
g=5 h=-1 k=-3 l=7 p=-15
This gives A=-27, B=2, D=-32, E=-96, F=-54, and C=-150, so dividing
the entire equation (2) by 2, the values of f and o must satisfy
(27-f)(75-o) = 1536
Translated back to the range 1-16, this condition is
(22-f')(46-o') = 384
which has just one solution in the range 1-16, namely [f'=10,o'=14],
in agreement with Durer's engraving. From these it's a simple matter
to fill in the remaining cells using relations such as a'+d'+p'+m'=34
and e+h = j+k, etc.
In a previous version of this note I asked if equation (2) necessarily
leads to a unique magic square. Russell Blau has shown that it doesn't,
by producing two distinct 4x4 magic squares with identical values of
g, h, k, l, and p. In terms of centralized values these squares are
-5 -13 5 13 7 -13 -7 13
-3 9 -9 3 9 -3 -9 3
1 -11 11 -1 -11 1 11 -1
7 15 -7 -15 -5 15 5 -15
For both of these squares we have g=-9, h=3, k=11, l=-1, p=-15, and
so A=-17, B=2, C=-26, D=-8, E=-40, F=14. Inserting these values into
(2) and dividing by 2 gives the condition on f and o:
(f - 17)(o - 13) = 160
The solutions of this equation in odd integers in the range -15 to
+15 are
(f,o) = (-3,5), (1,3), (7,-3), and (9,-7)
but only (-3,5) and (9,-7) give valid magic squares. This naturally
raises the question of how common this is, and whether there can be
more than two solutions for a given set of parameters (g,h,k,l,p).
To answer these questions I checked all 524160 permutations of 16
numbers taken five at a time, and determined how many (if any) valid
solutions they each give. It turns out that 4232 of those sets of
five elements leads to one or more valid magic squares, as summarized
in the table below:
Sets of Five Number of
Numbers Leading Distinct
to k Valid Magic
k Magic Squares Squares
--- --------------- ---------
1 2176 2176
2 1656 3312
3 80 240
4 304 1216
5 0 0
6 16 96
----- -----
4232 7040
This accounts for all 7040 of the 4x4 magic squares. Of course, each
of these can be oriented in four ways, and flipped over for four more
ways, so there are really just 7040/8 = 880 distinct 4x4 magic squares
up to rotations and reflections. Incidentally, here's an example of
SIX distinct squares for a single set of parameters {g,h,k,l,p}:
1 -9 -7 15 1 -7 -9 15 -3 -13 1 15
13 3 -11 -5 13 3 -11 -5 9 7 -11 -5
-13 -3 11 5 -13 -3 11 5 -9 -7 11 5
-1 9 7 -15 -1 7 9 -15 3 13 -1 -15
-3 1 -13 15 -9 -7 1 15 -9 1 -7 15
9 7 -11 -5 3 13 -11 -5 3 13 -11 -5
-9 -7 11 5 -3 -13 11 5 -3 -13 11 5
3 -1 13 -15 9 7 -1 -15 9 -1 7 -15
This is a degenerate case, in the sense that it gives A=-19, D=-8,
and B=C=E=F=0, so the relation between f and o is identically
satisfied, and therefore is of no use.
A couple of unanswered questions are: What's the simplest equation
that relates these five parameters (analagous to (1) for 3x3
squares)? Does every lattice point of that surface correspond
to a rotation or reflection of the square?
For more on magic squares, see
The Determinants of 4x4 Magic Squares
Magic Square of Squares
Orthomagic Square of Squares
Automedian Triangles, Eigen Vectors, and Magic Squares
Franklin's Magic Squares
These two ovals intersect at the lattice points. The quartic (2)
happens to have a nice solution in radicals, and the four roots
are all similar to the one appearing in the figure above, with
various signs. We can eliminate b from equations (1) and (2) by
solving each of them for b and setting the results equal. Then
with a little manipulation we arrive at the condition
a^4 - 10a^2 + 9 = (a^2 - 1)(a^2 - 9) = 0
which shows that the value of "a" (which appears in a corner of the
3x3 magic square) must be +-1 or +-3, and those are indeed the four
corner values for the 3x3 magic square, and all the remaining entries
are linearly related to these. Thus we have completely solved for
the entries of a 3x3 magic square. Of course, there is essentially
only one such square, so our solution is unique (up to rotations and
reflections).
For a less trivial case, consider the general 4x4 magic square
a b c d
e f g h
i j k l
m n o p
For even-order squares the quantity (N^2+1)/2 is a half-integer, so
in these cases we convert the original term x' in the range 1-16 to
the corresponding centralized term x in the range -(N^2-1) to +(N^2-1)
by applying the transformation x = 2x'-(N^2+1). Thus, with 4x4 magic
squares, instead of working with the values 1 through 16 we work with
signed odd integers -15,-13,..., +15.
Making use of the algebraic conditions on these 16 variables, we find
that a square can often be determined by the values assigned to just
5 elements (but see below for exceptions). This is because, given the
centralized values of g, h, k, l, and p, the values of f and o must
satisfy the equation
(f+A)(Bo+C) = DE (2)
where
A = 2p+k+l+h B = g+k D = A-g C = E+F
E = (l+k)(l+h) + p(g+h+l+k) F = (k+p)(k+g) + k(l+h)
To illustrate, consider the square in Albrecht Durer's engraving
"Melencolia", which has
g'=11 h'=8 k'=7 l'=12 p'=1
or, in centralized terms
g=5 h=-1 k=-3 l=7 p=-15
This gives A=-27, B=2, D=-32, E=-96, F=-54, and C=-150, so dividing
the entire equation (2) by 2, the values of f and o must satisfy
(27-f)(75-o) = 1536
Translated back to the range 1-16, this condition is
(22-f')(46-o') = 384
which has just one solution in the range 1-16, namely [f'=10,o'=14],
in agreement with Durer's engraving. From these it's a simple matter
to fill in the remaining cells using relations such as a'+d'+p'+m'=34
and e+h = j+k, etc.
In a previous version of this note I asked if equation (2) necessarily
leads to a unique magic square. Russell Blau has shown that it doesn't,
by producing two distinct 4x4 magic squares with identical values of
g, h, k, l, and p. In terms of centralized values these squares are
-5 -13 5 13 7 -13 -7 13
-3 9 -9 3 9 -3 -9 3
1 -11 11 -1 -11 1 11 -1
7 15 -7 -15 -5 15 5 -15
For both of these squares we have g=-9, h=3, k=11, l=-1, p=-15, and
so A=-17, B=2, C=-26, D=-8, E=-40, F=14. Inserting these values into
(2) and dividing by 2 gives the condition on f and o:
(f - 17)(o - 13) = 160
The solutions of this equation in odd integers in the range -15 to
+15 are
(f,o) = (-3,5), (1,3), (7,-3), and (9,-7)
but only (-3,5) and (9,-7) give valid magic squares. This naturally
raises the question of how common this is, and whether there can be
more than two solutions for a given set of parameters (g,h,k,l,p).
To answer these questions I checked all 524160 permutations of 16
numbers taken five at a time, and determined how many (if any) valid
solutions they each give. It turns out that 4232 of those sets of
five elements leads to one or more valid magic squares, as summarized
in the table below:
Sets of Five Number of
Numbers Leading Distinct
to k Valid Magic
k Magic Squares Squares
--- --------------- ---------
1 2176 2176
2 1656 3312
3 80 240
4 304 1216
5 0 0
6 16 96
----- -----
4232 7040
This accounts for all 7040 of the 4x4 magic squares. Of course, each
of these can be oriented in four ways, and flipped over for four more
ways, so there are really just 7040/8 = 880 distinct 4x4 magic squares
up to rotations and reflections. Incidentally, here's an example of
SIX distinct squares for a single set of parameters {g,h,k,l,p}:
1 -9 -7 15 1 -7 -9 15 -3 -13 1 15
13 3 -11 -5 13 3 -11 -5 9 7 -11 -5
-13 -3 11 5 -13 -3 11 5 -9 -7 11 5
-1 9 7 -15 -1 7 9 -15 3 13 -1 -15
-3 1 -13 15 -9 -7 1 15 -9 1 -7 15
9 7 -11 -5 3 13 -11 -5 3 13 -11 -5
-9 -7 11 5 -3 -13 11 5 -3 -13 11 5
3 -1 13 -15 9 7 -1 -15 9 -1 7 -15
This is a degenerate case, in the sense that it gives A=-19, D=-8,
and B=C=E=F=0, so the relation between f and o is identically
satisfied, and therefore is of no use.
A couple of unanswered questions are: What's the simplest equation
that relates these five parameters (analagous to (1) for 3x3
squares)? Does every lattice point of that surface correspond
to a rotation or reflection of the square?
For more on magic squares, see
The Determinants of 4x4 Magic Squares
Magic Square of Squares
Orthomagic Square of Squares
Automedian Triangles, Eigen Vectors, and Magic Squares
Franklin's Magic Squares
Return to MathPages Main Menu
 These two ovals intersect at the lattice points. The quartic (2)
happens to have a nice solution in radicals, and the four roots
are all similar to the one appearing in the figure above, with
various signs. We can eliminate b from equations (1) and (2) by
solving each of them for b and setting the results equal. Then
with a little manipulation we arrive at the condition
a^4 - 10a^2 + 9 = (a^2 - 1)(a^2 - 9) = 0
which shows that the value of "a" (which appears in a corner of the
3x3 magic square) must be +-1 or +-3, and those are indeed the four
corner values for the 3x3 magic square, and all the remaining entries
are linearly related to these. Thus we have completely solved for
the entries of a 3x3 magic square. Of course, there is essentially
only one such square, so our solution is unique (up to rotations and
reflections).
For a less trivial case, consider the general 4x4 magic square
a b c d
e f g h
i j k l
m n o p
For even-order squares the quantity (N^2+1)/2 is a half-integer, so
in these cases we convert the original term x' in the range 1-16 to
the corresponding centralized term x in the range -(N^2-1) to +(N^2-1)
by applying the transformation x = 2x'-(N^2+1). Thus, with 4x4 magic
squares, instead of working with the values 1 through 16 we work with
signed odd integers -15,-13,..., +15.
Making use of the algebraic conditions on these 16 variables, we find
that a square can often be determined by the values assigned to just
5 elements (but see below for exceptions). This is because, given the
centralized values of g, h, k, l, and p, the values of f and o must
satisfy the equation
(f+A)(Bo+C) = DE (2)
where
A = 2p+k+l+h B = g+k D = A-g C = E+F
E = (l+k)(l+h) + p(g+h+l+k) F = (k+p)(k+g) + k(l+h)
To illustrate, consider the square in Albrecht Durer's engraving
"Melencolia", which has
g'=11 h'=8 k'=7 l'=12 p'=1
or, in centralized terms
g=5 h=-1 k=-3 l=7 p=-15
This gives A=-27, B=2, D=-32, E=-96, F=-54, and C=-150, so dividing
the entire equation (2) by 2, the values of f and o must satisfy
(27-f)(75-o) = 1536
Translated back to the range 1-16, this condition is
(22-f')(46-o') = 384
which has just one solution in the range 1-16, namely [f'=10,o'=14],
in agreement with Durer's engraving. From these it's a simple matter
to fill in the remaining cells using relations such as a'+d'+p'+m'=34
and e+h = j+k, etc.
In a previous version of this note I asked if equation (2) necessarily
leads to a unique magic square. Russell Blau has shown that it doesn't,
by producing two distinct 4x4 magic squares with identical values of
g, h, k, l, and p. In terms of centralized values these squares are
-5 -13 5 13 7 -13 -7 13
-3 9 -9 3 9 -3 -9 3
1 -11 11 -1 -11 1 11 -1
7 15 -7 -15 -5 15 5 -15
For both of these squares we have g=-9, h=3, k=11, l=-1, p=-15, and
so A=-17, B=2, C=-26, D=-8, E=-40, F=14. Inserting these values into
(2) and dividing by 2 gives the condition on f and o:
(f - 17)(o - 13) = 160
The solutions of this equation in odd integers in the range -15 to
+15 are
(f,o) = (-3,5), (1,3), (7,-3), and (9,-7)
but only (-3,5) and (9,-7) give valid magic squares. This naturally
raises the question of how common this is, and whether there can be
more than two solutions for a given set of parameters (g,h,k,l,p).
To answer these questions I checked all 524160 permutations of 16
numbers taken five at a time, and determined how many (if any) valid
solutions they each give. It turns out that 4232 of those sets of
five elements leads to one or more valid magic squares, as summarized
in the table below:
Sets of Five Number of
Numbers Leading Distinct
to k Valid Magic
k Magic Squares Squares
--- --------------- ---------
1 2176 2176
2 1656 3312
3 80 240
4 304 1216
5 0 0
6 16 96
----- -----
4232 7040
This accounts for all 7040 of the 4x4 magic squares. Of course, each
of these can be oriented in four ways, and flipped over for four more
ways, so there are really just 7040/8 = 880 distinct 4x4 magic squares
up to rotations and reflections. Incidentally, here's an example of
SIX distinct squares for a single set of parameters {g,h,k,l,p}:
1 -9 -7 15 1 -7 -9 15 -3 -13 1 15
13 3 -11 -5 13 3 -11 -5 9 7 -11 -5
-13 -3 11 5 -13 -3 11 5 -9 -7 11 5
-1 9 7 -15 -1 7 9 -15 3 13 -1 -15
-3 1 -13 15 -9 -7 1 15 -9 1 -7 15
9 7 -11 -5 3 13 -11 -5 3 13 -11 -5
-9 -7 11 5 -3 -13 11 5 -3 -13 11 5
3 -1 13 -15 9 7 -1 -15 9 -1 7 -15
This is a degenerate case, in the sense that it gives A=-19, D=-8,
and B=C=E=F=0, so the relation between f and o is identically
satisfied, and therefore is of no use.
A couple of unanswered questions are: What's the simplest equation
that relates these five parameters (analagous to (1) for 3x3
squares)? Does every lattice point of that surface correspond
to a rotation or reflection of the square?
For more on magic squares, see
The Determinants of 4x4 Magic Squares
Magic Square of Squares
Orthomagic Square of Squares
Automedian Triangles, Eigen Vectors, and Magic Squares
Franklin's Magic Squares
These two ovals intersect at the lattice points. The quartic (2)
happens to have a nice solution in radicals, and the four roots
are all similar to the one appearing in the figure above, with
various signs. We can eliminate b from equations (1) and (2) by
solving each of them for b and setting the results equal. Then
with a little manipulation we arrive at the condition
a^4 - 10a^2 + 9 = (a^2 - 1)(a^2 - 9) = 0
which shows that the value of "a" (which appears in a corner of the
3x3 magic square) must be +-1 or +-3, and those are indeed the four
corner values for the 3x3 magic square, and all the remaining entries
are linearly related to these. Thus we have completely solved for
the entries of a 3x3 magic square. Of course, there is essentially
only one such square, so our solution is unique (up to rotations and
reflections).
For a less trivial case, consider the general 4x4 magic square
a b c d
e f g h
i j k l
m n o p
For even-order squares the quantity (N^2+1)/2 is a half-integer, so
in these cases we convert the original term x' in the range 1-16 to
the corresponding centralized term x in the range -(N^2-1) to +(N^2-1)
by applying the transformation x = 2x'-(N^2+1). Thus, with 4x4 magic
squares, instead of working with the values 1 through 16 we work with
signed odd integers -15,-13,..., +15.
Making use of the algebraic conditions on these 16 variables, we find
that a square can often be determined by the values assigned to just
5 elements (but see below for exceptions). This is because, given the
centralized values of g, h, k, l, and p, the values of f and o must
satisfy the equation
(f+A)(Bo+C) = DE (2)
where
A = 2p+k+l+h B = g+k D = A-g C = E+F
E = (l+k)(l+h) + p(g+h+l+k) F = (k+p)(k+g) + k(l+h)
To illustrate, consider the square in Albrecht Durer's engraving
"Melencolia", which has
g'=11 h'=8 k'=7 l'=12 p'=1
or, in centralized terms
g=5 h=-1 k=-3 l=7 p=-15
This gives A=-27, B=2, D=-32, E=-96, F=-54, and C=-150, so dividing
the entire equation (2) by 2, the values of f and o must satisfy
(27-f)(75-o) = 1536
Translated back to the range 1-16, this condition is
(22-f')(46-o') = 384
which has just one solution in the range 1-16, namely [f'=10,o'=14],
in agreement with Durer's engraving. From these it's a simple matter
to fill in the remaining cells using relations such as a'+d'+p'+m'=34
and e+h = j+k, etc.
In a previous version of this note I asked if equation (2) necessarily
leads to a unique magic square. Russell Blau has shown that it doesn't,
by producing two distinct 4x4 magic squares with identical values of
g, h, k, l, and p. In terms of centralized values these squares are
-5 -13 5 13 7 -13 -7 13
-3 9 -9 3 9 -3 -9 3
1 -11 11 -1 -11 1 11 -1
7 15 -7 -15 -5 15 5 -15
For both of these squares we have g=-9, h=3, k=11, l=-1, p=-15, and
so A=-17, B=2, C=-26, D=-8, E=-40, F=14. Inserting these values into
(2) and dividing by 2 gives the condition on f and o:
(f - 17)(o - 13) = 160
The solutions of this equation in odd integers in the range -15 to
+15 are
(f,o) = (-3,5), (1,3), (7,-3), and (9,-7)
but only (-3,5) and (9,-7) give valid magic squares. This naturally
raises the question of how common this is, and whether there can be
more than two solutions for a given set of parameters (g,h,k,l,p).
To answer these questions I checked all 524160 permutations of 16
numbers taken five at a time, and determined how many (if any) valid
solutions they each give. It turns out that 4232 of those sets of
five elements leads to one or more valid magic squares, as summarized
in the table below:
Sets of Five Number of
Numbers Leading Distinct
to k Valid Magic
k Magic Squares Squares
--- --------------- ---------
1 2176 2176
2 1656 3312
3 80 240
4 304 1216
5 0 0
6 16 96
----- -----
4232 7040
This accounts for all 7040 of the 4x4 magic squares. Of course, each
of these can be oriented in four ways, and flipped over for four more
ways, so there are really just 7040/8 = 880 distinct 4x4 magic squares
up to rotations and reflections. Incidentally, here's an example of
SIX distinct squares for a single set of parameters {g,h,k,l,p}:
1 -9 -7 15 1 -7 -9 15 -3 -13 1 15
13 3 -11 -5 13 3 -11 -5 9 7 -11 -5
-13 -3 11 5 -13 -3 11 5 -9 -7 11 5
-1 9 7 -15 -1 7 9 -15 3 13 -1 -15
-3 1 -13 15 -9 -7 1 15 -9 1 -7 15
9 7 -11 -5 3 13 -11 -5 3 13 -11 -5
-9 -7 11 5 -3 -13 11 5 -3 -13 11 5
3 -1 13 -15 9 7 -1 -15 9 -1 7 -15
This is a degenerate case, in the sense that it gives A=-19, D=-8,
and B=C=E=F=0, so the relation between f and o is identically
satisfied, and therefore is of no use.
A couple of unanswered questions are: What's the simplest equation
that relates these five parameters (analagous to (1) for 3x3
squares)? Does every lattice point of that surface correspond
to a rotation or reflection of the square?
For more on magic squares, see
The Determinants of 4x4 Magic Squares
Magic Square of Squares
Orthomagic Square of Squares
Automedian Triangles, Eigen Vectors, and Magic Squares
Franklin's Magic Squares