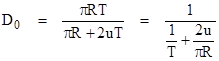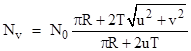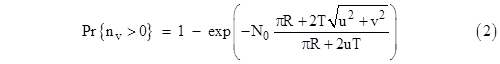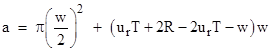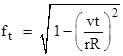Hail Encounters

What is the probability of an airplane being in intense hail continuously for a given period of time? For purposes of the analysis, make the following assumptions:

(a)  Every hail storm is circular with radius R and moves in a straight line with

      velocity u. Also, every hail storm exists for a length of time T.

(b)  The initial positions of storms are randomly and uniformly distributed over

       an infinite flat plane and throughout time. Also, the directions of motion of

       a storm is randomly and uniformly distributed from 0 to 2π.

(c)  Storms occur at an average rate such that a stationary observer has an

      expected value of N₀ storms per unit time, and every stationary point has an

      equal probability of being in a storm at any randomly selected instant.

(d)  An airplane is modeled as a moving observer travelling in a straight line with

       velocity v. The direction of motion is uncorrelated with the location or

       direction of motion of any storm.

First we will determine the probability that a moving observer will encounter a storm at least once during a given time interval. Then we will impose the requirement that the duration of the encounter must be at least t.

Since the probability of a storm at any given instant is independent of position, it follows that every observer (moving or stationary) has the same expected total duration of time-in-storm per unit time. However, the expected number of encounters will depend on the relative motion of storm and observer, and on the spatial and temporal extent of storms. Letting N_v denote the expected number of storms encounters per unit time for an observer moving with velocity v, and letting D_v denote the average duration of each encounter, we have

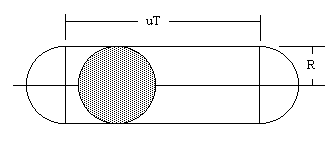
where D₀ is the average duration of a storm for a stationary observer. The value of D₀ can be deduced from the diagram below.

The total swept area of a storm is πR² + 2RuT, and the portion of that region in a storm at any given time is πR². The total (area)(time) of the storm is πR²T, and this must equal the product of the total swept area times the average duration for which each encountered point is in the storm. That is

so we have

If an observer has velocity v (relative to the ground) at an angle θ relative to the storm's direction of motion, then the relative velocity between storm and observer is the vector sum of magnitude

Therefore, we have

Integrating this over θ from 0 to 2π and then dividing the result by 2π gives the average duration of encounter for observers moving with velocity v and arbitrary direction θ

which, of course, reduces to D₀ when v = 0. We can now solve (1) for N_v, which gives

This is the expected number of encounters per unit time for a moving observer. Therefore, letting n_v denote the actual number of encounters per unit time for an observer moving with a velocity v, Poisson's distribution gives the probability of one or more encounters as

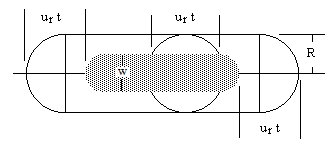
To determine the probability of at least one encounter that lasts for a duration at least equal to some specified time t, we must find the fraction of all encounters having duration greater than or equal to t. This can be deduced from the diagram below.

The shaded area is the locus of points that are in the storm for at least the time t. This region has an area of

where

Obviously these equations assume the inequalities t < T and t < 2T/u_r. If either of these is false, then no observer will be in the storm for a time greater than t.

Now, if the storm velocity u can be considered negligible compared to the observer's velocity, and if T/t is greater than about 30, then the ratio of the total number of encounters to those that last for at least a time t is given by

Using these same assumptions, the adjustment to the expected number of encounters due to the motion of the observer given in equation (2) reduces to

and the equation for the probability of at least one encounter lasting for at least a time t becomes

Return to MathPages Main Menu