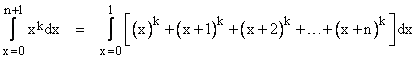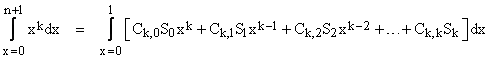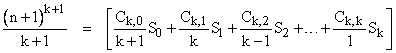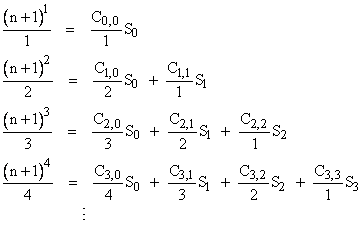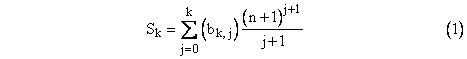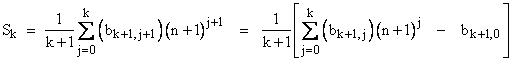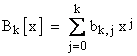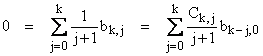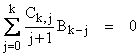Sums of Powers

Let S_k(n) denote the sum of the kth powers of the first n integers. (For convenience we will define S₀ = n+1.) It’s fairly easy to determine the explicit formula for these sums directly from the definition. For example, by the definition of the sum of cubes function we have

so it's clear that S₃ is a polynomial in n of finite degree in n. Also, the asymptotic growth rate obviously doesn't exceed the 4th power of n, so we expect that S₃ can be expressed in the form

for some constants A,B,C,D,E. We immediately see that E must be zero to give S₃(0) = 0. Furthermore, from the defining relation we have

Expanding each of the binomials, collecting terms by powers of n, and setting the coefficient of each power to zero, we find that A = 1/4, B = 1/2, C = 1/4, and D = 0, so the formula for the sum of the first n cubes is

The formulas for the sums of other powers can be derived in the same purely algebraic way. (For a discussion of a generalization of this approach, see the note on Sums and Differences of Discrete Functions.) However, it’s natural to wonder whether these formulas might be derivable in terms of the integral of x^k from x = 0 to n, since evaluating this integral is trivial. In fact, we can see that the first term in the formula for S₃(n) is simply the integral of x³ from x = 0 to n. (In a sense, this was the justification for our presumption that S_k(n) is a polynomial of degree k+1.) On the other hand, the summation has some additional terms that don’t appear in the integral, so we can’t simply equate the sum to the corresponding integral.

To see exactly how sums of powers are related to integrals of powers, consider the integral

Letting C_m,n denote binomial coefficients, we can expand the binomials and collect terms by powers of x to give

where we have omitted the arguments on S_k, with the understanding that they represent S_k(n). Carrying out the integrations on both sides, we get

This equation is valid for any non-negative integer k, so it gives the following infinite sequence of equations involving the sums of powers:

We can solving the first N of these equations to give expressions for S₀, S₁, …, S_N-1. For example, to find formulas for S₀ through S₆, we simply solve the system of equations

Solving this system of equations by inverting the coefficient matrix on the left side, we get

Letting b_k,j denote the element in the jth column of the kth row of the coefficient matrix, we can write the sums of the kth powers of the first n integers as

Thus we have

and so on. Expanding the binomials and simplifying, these expressions reduce to

and so on. It appears that Sk for every positive even value of k is divisible by the factors n, (n+1), and (2n+1). It would be interesting to know what other divisibility patterns these sums possess. Also, notice that the elements of the coefficient array satisfy the relation

and using this relation we can re-write equation (1) as

Therefore, letting B_k[x] denote the polynomial

we can write the sum of the kth powers of the first n non-negative integers succinctly as

Notice also that equation (2) can be written as

from which it follows that

Thus we can express all the b_k,j values in terms of binomial coefficients and the values of b_0,0, b_1,0, b_2,0, b_3,0, and so on. These numbers are called the Bernoulli numbers, usually denoted by B_k = b_k,0. To easily generate these numbers (without inverting large matrices), consider our previous expression for S_k in the special case of n = 0, so that S_k = 0 for all k > 0. In this case we have

Hence we have the recurrence relation

For example, given the values of B₀ = 1, B₁ = -1/2, B₂ = 1/6, B₃ = 0, we can compute B₄ from the relation

Inserting the values of B₀ through B₃, we find that B4 equals -1/30.

The Bernoulli numbers were introduced by Jacques Bernoulli around 1690 in a short paper on computing the sums of powers. He was obviously pleased with his formulas when he wrote

With the help of [these formulas] it took me less than half of a quarter of an hour to find that the 10th powers of the first 1000 numbers being added together will yield the sum

                                        91409924241424243424241924242500

From this it will become clear how useless was the work of Ismael Bullialdus spent on the compilation of his voluminous Arithmetica Infinitorum in which he did nothing more than compute with immense labor the sums of the first six powers, which is only a part of what we have accomplished in the space of a single page.

(One senses how distasteful Jacques found it to belittle one of his colleagues.) Even with the formula for the sums of 10th powers, it’s impressive that Bernoulli could compute that number by hand in 7.5 minutes. Of course, using N=1000 in the base 10 probably made it easier. In any case, one must agree that the labor Bullialdus put into his tables of sums of powers was wasted, considering how easy it is to derive the explicit formulas for these sums.

Incidentally, given the formulas for the sums of powers, it follows that if f(k) is any polynomial function of k, we can easily express the sum of f(k) for k = 0 to n by considering the sums of each separate term, which are pure sums of powers. This is the origin of the Euler-Maclaurin formula, which is just a generalization of Bernoulli’s formula, replacing x^k with an arbitrary function f(x).

Return to MathPages Main Menu