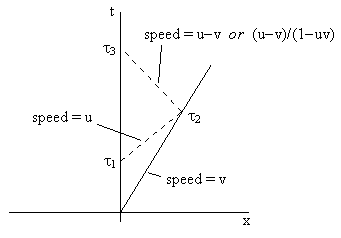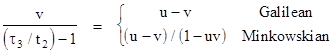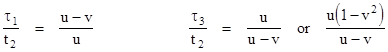Reflecting on the Geometric Mean

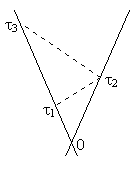
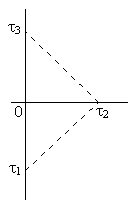
Discussions of special relativity often refer to the use of clocks and reflected light signals for the evaluation of spacetime intervals. For example, suppose two identical clocks are moving uniformly with speeds +v and −v along the x axis of a given inertial coordinate system, and these clocks are set to zero at the intersection of their worldlines. When the leftward clock indicates the proper time τ₁, it emits a pulse of light, which bounces off the rightward clock when that clock indicates τ₂, and arrives back at the leftward clock when that clock reads τ₃. This is illustrated in the drawing below.

By similar triangles we immediately have τ₂/τ₁ = τ₃/τ₂, and thus τ₂² = τ₁τ₃. Of course, this same relation holds good in Galilean spacetime as well (not to mention Euclidean plane geometry, using distances instead of time intervals), and the reflected signal need not be a light pulse. Any object moving at the same speed (angle) in both directions with respect to this coordinate system would serve just as well, and would lead to the same result that τ₂ is the geometric mean of τ₁ and τ₃. Naturally if we apply any Minkowskian, Galilean, or Euclidean transformation (respectively), the pictorial angles of the lines will differ, but the three absolute intervals will remain unchanged.

It is, of course, possible to distinguish between the Galilean and Minkowskian cases based just on the values of the elapsed times, provided we know the relative speeds of the clocks and the signal. In Galilean spacetime each proper time τ_j equals the coordinate time t_j, whereas in Minkowski spacetime it equals (t_j² - x_j²)^1/2 where x_j = ±v t_j. Hence the proper time τ_j in Minkowski spacetime is t_j(1 - v²)^1/2. This might seem to imply that the ratios of proper times are the same in the Galilean and Minkowskian cases, but in fact we have not made a valid comparison for equal relative speeds between the clocks. In this example each clock is moving with speed v away from the midpoint, which implies that the relative speed is 2v in the Galilean case, but only 2v/(1 + v²) in the Minkowskian case.

To give a valid comparison for equal relative speeds between the clocks, let's transform the events to a system of coordinate such that the left-hand clock is stationary and the right-hand clock is moving at the speed v. Now this v represents magnitude of the actual relative speed between the two clocks. We now stipulate that the original signal is moving with speed u relative to the left-hand clock, and the reflected signal is moving with speed -u relative to the right-hand clock. The situation is illustrated in the figure below.

The speed, with respect to these coordinates, of the reflected signal is what distinguishes the Galilean from the Minkowskian case. Letting x₂ and t₂ denote the coordinates of the reflection event, and noting that τ₁ = t₁ and τ₃ = t₃, we have v = x₂/t₂ and u = x₂/(t₂-τ₁). We also have

Dividing the numerator and denominator of the expression for u by t₂, and replacing x₂/t₂ with v, gives u = v/[1-(τ₁/t₂)]. Likewise the above expressions can be written as

Solving these equations for the time ratios, we have

Consequently, depending on whether the metric is Galilean or Minkowskian, the ratio of τ₃ over τ₁ is given by

respectively. If u happens to be unity (meaning that the signals propagate at the speed of light), these expressions reduce to the squares of the Galilean and relativistic Doppler shift factors, i.e., 1/(1-v)² and (1+v)/(1-v).

Another distinguishing factor between the two metrics is that with the Minkowski metric the speed of light is invariant with respect to any system of inertial coordinates, so (arguably) we can even say that it represents the same "u" relative to a spacelike interval as it does relative to a timelike interval, in order to adhere to our stipulation that the reflected signal has the speed u relative to "the rest frame of the right-hand clock". Of course, a spacelike interval cannot actually be the worldline of a clock (or any other material object), but the invariance of the speed of light under Minkowskian transformations enables us to rationally apply the same "geometric mean" formula to determine the magnitudes of spacelike intervals, provided we use light-like signals, as illustrated below.

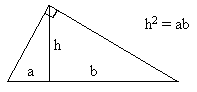
In this case we have τ₁ = -τ₃, so τ₂² = -τ₃², meaning that squared spacelike intervals are negative. Notice that, as drawn, the signal and its reflection in the above figure are orthogonal, and the "height" of the right triangle is (up to sign) the geometric mean of the partition of the base formed by the perpendicular from the vertex. This recalls a simple fact from plane Euclidean geometry, which is really just an alternative way of expressing the Pythagorean theorem. As shown in the figure below, the height of a right triangle is the geometric mean of the partition of its base (hypotenuse) formed by the perpendicular from the vertex.

This shows that for three line segments in the Euclidean plane, if one of them is the geometric mean of the other two, then it's possible to arrange those vectors so that they all emanate from a single point and the mean vector is the height and the other two form the base of a right triangle.

More generally, let P₁, P₂, P₃ denote three fixed points on a two-dimensional surface, and suppose the line element of this surface in terms of x,y coordinates is

where a,b are constants. If s₁, s₂, s₃ are the distances from the origin to the three given points, under what conditions do we have the relation s₂² = ±s₁s₃? Squaring both sides of this relation and letting x_j,y_j denote the coordinates of P_j, we have

The first product on the right hand side can be expanded into a quadratic form by means of the identity

If P₁ and P₃ are co-linear with the origin, then the last term in this expression vanishes, so we can revert back to the non-squared expressions, and we have

Clearly a sufficient condition for this to vanish, regardless of the values of the metric coefficients a,b, is x₂² = x₁x₃ and y₂² = y₁y₃, but since P₁ and P₃ are assumed to be co-linear with the origin, this amounts to assuming that P₂ is also co-linear, so it's a degenerate solution. However, taking advantage of the co-linearity of P₁ and P₃ with the origin, we can arrange by a suitable transformation for these points to fall on the y axis, so we have x₁ = x₃ = 0. Also, if we stipulate that the "signals" have unit velocity, it follows that y₁ = y₂ - x₂ and y₃ = y₂ + x₂. Making these substitutions, we arrive at

The right hand side is just the squared magnitude of each of the signal interval. The Minkowski metric has a + b = 0, so the signal intervals have null magnitude, and s₂ is the geometric mean of s₁ and s₃. This type of analysis doesn't apply to the Galilean situation, because there is no unified Galilean spacetime metric, i.e., the space and time dimensions are completely independent.

Return to MathPages Main Menu