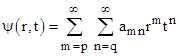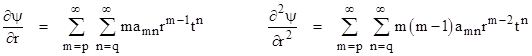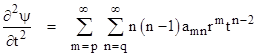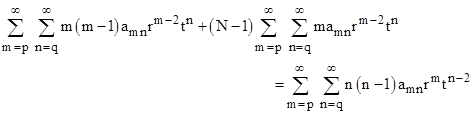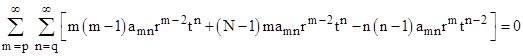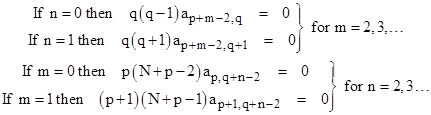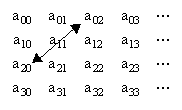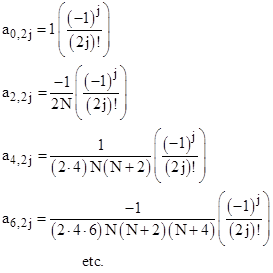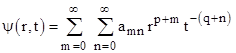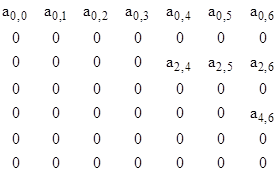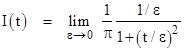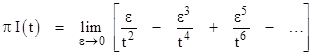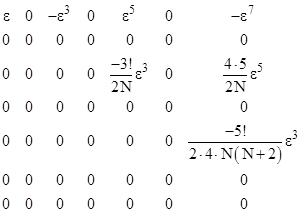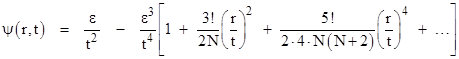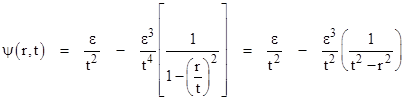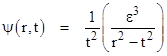Series Solutions of the Wave Equation

The spherically symmetrical wave equation in N space dimensions and 1 time dimension is

Suppose a solution of this equation has the form

where the fixed integers p and q represent the lowest powers of r and t (respectively) appearing in any term with a non-zero coefficient. Hence we have a_mq ≠ 0 for some index m, and we have a_pn ≠ 0 for some index n. The first and second partial derivatives of this wave function with respect to r are

Likewise the second partial derivative of the wave function with respect to t is

Substituting for these partials into equation (1) gives

Notice that we have absorbed the factor 1/r in the second term into the summation. Combining all the summations, we have

In order to collect terms by powers of r and t we must take the right-most terms with the indices m–2 and n+2, which means the factor becomes (n+2)(n+1). Hence, setting the coefficients of every term in the overall expansion to zero gives the condition

If, instead of numbering the indices m,n from p,q to infinity, we number them from 0 to infinity, then we must replace each m with p+m and each n with q+n respectively. On this basis the conditions are expressed as

To enhance the symmetry, we can replace n with n–2, allowing us to write the conditions in the form

We know that a_jk = 0 if j<p or k<q, so the left sides of these conditions vanish when n = 0 or 1, and the right sides vanish and when m = 0 or 1. Consequently we have the four conditions

We also know that a_jq is non-zero for some j, and a_pk is non-zero for some k. It follows from the above conditions for n = 0 and m = 0 that q(q–1) = 0 and p(N+p–2) = 0. Consequently, we must have q = 0 or 1, and p = 0 or 2–N, so there are four possible combinations of least indices.

Incidentally, this implies that it's possible for ψ(0,t) to be an odd or an even function, depending on whether q is 0 or 1, and ψ(r,0) can also be an odd or even function if the number N of spatial dimensions is odd. The general solution can be expressed as a sum of separable terms of the form f(t)g(r), where f and g have one of the four combinations of possible q and p values, so if N is odd we a complete basis of odd and even functions for the solution. This is why, in an odd number of spatial dimensions, we can propagate arbitrary waveforms, and the strong form of Huygens' Principle applies. However, if the number N of spatial dimensions is even, both possible indices p = 0 and p = 2–N for the radial exponent are even. Consequently we cannot have a purely odd function of r, so we do not have a complete basis for solutions. Only a restricted set of radial waveforms can propagate in a space with an even number of dimensions, and these imply disturbances inside the future null cone of a pulse. Therefore, the strong form of Huygen's Principle is not satisfied in an even-dimensional space.

In the case p = q = 0, the above conditions do not constrain the values of a_j,q, a_j,q+1, and a_p,j for any j. However, they do require that all the coefficients a_1,j vanish (assuming N is not equal to 1). The recursive relation in this case reduces to

We can make an array of the coefficients as shown below.

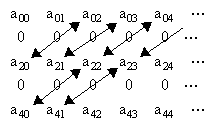
The arrow indicates the pairs of coefficients that are related by the recurrence formula. One consequence is that, since all the a_1j coefficients are zero, all the a_3j coefficients must also vanish, and in general all the a_mj coefficients for odd indices m must vanish. Therefore the array of coefficients looks like this

The first row represents the coefficients of the wave function at the spatial origin as a function of time, i.e., the coefficients of ψ(0,t). Likewise the first column represents the coefficients of the wave function at the initial instant as a function of radial position, i.e., the coefficients of ψ(r,0). The second column is essentially the rate of change of the wave function at the initial instant as a function of radial position.

The form of the recursive relation implies that we can fully specify the entire wave function (for the case p = q = 0) simply by specifying the value at the origin for all time. In other words, we are free to specify the top row of coefficients a₀₀, a₀₁, a₀₂,..., and these are sufficient to compute all the remaining coefficients, as indicates by the arrows. On the other hand, the first column of coefficients, by itself, is not sufficient to determine the wave function, because those values determine a_0j only for even indices j. In order to fix the values of a_0j for odd j we must specify the second column of coefficients, i.e., the rate of change of the wave function at the initial instant.

Notice that if the initial rate of change of the wave function is zero, then all the coefficients of odd powers of t in ψ(0,t) to vanish, which implies that ψ is an even function of time, i.e., symmetrical with respect to time about any instant in which the wave function is stationary.

To illustrate, suppose the wave function at the spatial origin is ψ(0,t) = cos(t). This implies that the first row of coefficients are

Using the recurrence formula, the next row of non-zero coefficients is

These two rows, and the subsequent rows, can be summarized as follows

This shows that the overall wave function is separable, i.e., we can factor cos(t) out of these coefficients, and we have ψ(r,t) = cos(t) f(r) where

If N = 1 this function is simply cos(r), and if N = 3 this function is sin(r)/r. If N = 2 this function is the zeroth-order Bessel function, often denoted as J₀(r). (For more on this, see the article on “Huygens' Principle”.)

We can also derive the family of series solutions of the wave equation based on inverse powers of time, i.e., we can assume a wave function of the form

Using the same method as above, we arrive at the following conditions on the coefficients:

Since a_0,n is non-zero for some n, we must have p = 0 or else p = 2–N. Also, these conditions imply that a_j,0 = a_j,1 = a_j,2 = 0 for all j greater than 0, and they also imply that a_m,n = 0 for all odd indices m. Hence we have an array of coefficients of the form

and so on. If we take q = 2, the upper row of coefficients represents the wave function at the spatial origin of the form

It's interesting to consider the response to a unit "impulse" occurring at the spatial origin at time t = 0. An impulse can be represented by a scaled Cauchy function in the limit as the scale factor ε goes to zero, i.e.,

Expanding this into a power series in ε gives

Taking this as the wave function at the spatial origin, the coefficient array has the form

Collecting by powers of ε, the first two orders give the wave function

in the limit as ε approaches zero. Notice that if N = 3, the quantity in the square brackets is just a geometric series in (r/t)², so (formally) we have

For any non-zero value of t, the first term vanishes in the limit as ε goes to zero, and we are left with

This shows that, in the limit ε → 0, the wave function vanishes except on the "null cone" where r² – t² = 0. It also shows that if the ratio of ε³ to r² – t² goes to one on the null cone itself as ε goes to zero, then the magnitude of the wave function drops in proportion to 1/t² = 1/r².

Return to MathPages Main Menu