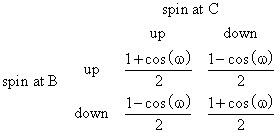|
Quantum Interactions on Null Surfaces |
|
|
|
What is the meaning of physical locality in Minkowski spacetime, given that for any two events A and B there exist other points C such that the spacetime intervals CA and CB are both zero? This immediately leads to the questions of whether physical effects can operate "in both directions" along a null interval, and hence whether locality is transitive. The space-time separation between the transmission and absorption of a photon is zero, so is there any reason not to expect that the exchange of a photon is conditioned by its reception just as it is conditioned by its emission? This is closely related to the Wheeler-Feynman "absorber theory" of advanced and retarded electromagnetic waves, although the Minkowski metric has similar implications for massive particles as well, noting that Schrödinger’s wave equations, like Maxwell's equations, work equally well forwards and backwards in time. Of course, on a macroscopic level we seem to only observe outward "retarded" waves, not inward "advanced" waves. |
|
|
|
Many suggestions have been made for interpretations of quantum mechanics (and relativity) along these lines, but perhaps the content of this kind of interpretation hasn't yet been fully and clearly articulated. The existing descriptions remind me somewhat of the old Lorentz theory of the electron around the turn of the century, which included length and time contractions, etc., but it wasn’t yet clear that they were dealing with a fundamental aspect of space and time that could be explained (and even deduced) very simply from a sound set of fundamental principles. |
|
|
|
Surprising as it seems, nearly a century after special relativity was first put forward, it could be argued that physicists have yet to fully grasp the physical significance of the Minkowski structure of spacetime, particularly the singularities in the pseudo-metric that represent null surfaces. For any two spacetime points A,B the intersection of the corresponding null cones is a quadratic surface: a hyperboloid if the interval AB is spacelike, an ellipsoid if AB is timelike, and a paraboloid if AB is lightlike. Of these three surfaces only the ellipsoid (corresponding to the intersection of time-like separated null cones) is finite. |
|
|
|
In conventional terms, suppose an electron is emitted from System X at point A and absorbed by System Y at point B, with no intermediate interactions. The interval AB is necessarily timelike, and the intersection between the null cones >A< and >B< is a closed ellipsoidal surface in spacetime. Relative to the frame of the interval AB this surface is simply a sphere of radius r = cT/2 (where T is the time interval between A and B) at the instant half-way between A and B. |
|
|
|
The interaction between Systems X and Y is symmetrical in time, and can be considered to originate on the surface of intersection between >A< and >B<. This surface consists of precisely all the points in spacetime that are null-separated from both A and B. Two equal and opposite electron waves "emanate" from this surface. The positive wave converges along the null cone >B< to point B, and the negative wave converges along the null cone >A< to point A. The net effect is to deduct an electron from System X at point A and add an electron to System Y at point B. |
|
|
|
This basic model can be used to represent all physical interactions, and gives results entirely consistent with observation. However, this view has the advantage that, because interactions occur along null absolute separations, all the familiar "quantum paradoxes" of locality vanish. To illustrate, consider the traditional EPR experiment in which two initially coupled particles are discharged from emitter A in opposite directions and are absorbed by spin- detecting sensors at locations B and C. If w denotes the difference between the spin-orientation test angles at sensors B and C, we expect the probabilities of the four possible outcomes to be as shown below |
|
|
|
|
|
|
|
The time-symmetric interpretation has no difficulty describing how such a correlation can be realized, because the discharge emanates from the surfaces of intersection >A<|>B< and >A<|>C<, both of which are on the null cone of A. The coupled discharge at A takes place only if/when two suitably correlated negative electron waves reach it simultaneously. These electron waves are correlated with the absorptions of the corresponding positive electron waves at sensors B and C because the two emanating surfaces are null-separated from points B and C. |
|
|