The 3m Halo

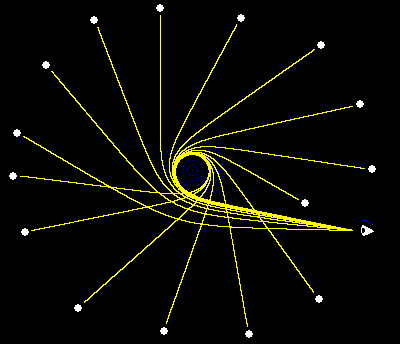
One of the most famous predictions of general relativity is that rays of light are curved when passing through a gravitational field, and we can even observe this deflection in the apparent positions of the stars near our Sun during an eclipse. Of course, the Sun’s gravitational field is relatively mild, so the amount of deflection for a ray of light grazing the Sun is only about 1.75 arc seconds. However, for a gravitating body such as a black hole, the paths of light can be curved much more. In fact, at a radius of 3m, where m is the mass of the body in geometrical units, a ray of light can orbit the body in a continuous loop (although the orbit is unstable). The figure below shows the actual paths of rays of light emanating from a ring of stars surrounding a black hole.

The symbolic “eye” in the lower right corner would “see” all the stars in this equatorial plane compressed and concentrated into a very small subtended arc just outside the 3m radius. (Of course, it would also see those same stars via direct light rays.) Interestingly, the eye could even see an image of itself near the 3m radius.

In theory, if the rays of light were infinitely fine and their directions of emission were continuously distributed as they emerge from their respective stars, the eye would see infinitely many copies of each star, because there would be a ray of light from each star that makes just one loop before reaching the eye, and another that makes two-loops, and another that makes three loops, and so on. This is shown by the fact that the integral for the angular travel of a null ray can be made arbitrarily great by making the perihelion distance arbitrarily close to 3m. (See the note on Bending Light for a derivation of this integral.)

However, there would presumably be some effective cutoff point, either due to the natural instability of the geodesic paths near the 3m radius, or to the discreteness of the photons, or to disturbing interactions with in-falling matter. Nevertheless, the gravitational field of the black hole serves to concentrate in-coming light from all directions (in the plane) into the small out-going arc near the 3m radius. Naturally the opposite point on the 3m radius would also emit concentrated light from the same plane, but for light rays making clock-wise loops. Also, the surrounding stars in other planes would each contribute infinitely many (or up to the cutoff point) copies of themselves, all reaching the eye by way of a small ring just outside the 3m radius of the black hole.

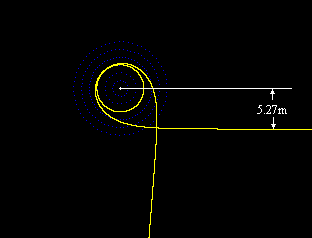
Actually the rays of light would emerge along paths that appear to originate at a radius of about 5.27m, because of the total deflection of the out-going paths as shown in the figure below.

Nevertheless, since the orbital radius of the light rays asymptotically approaches 3m as they circle the black hole, we will refer to it as the “3m halo”. A black hole located inside a distant galaxy would, in principle, collect images of each star in the galaxy and emit those images from near the 3m radius in every direction. As a result, we would expect the 3m radius surrounding the black hole to be as luminous as all the other stars in the galaxy combined. In fact, it would be even more luminous, because the 3m radius would collect copies of the star images in both the clockwise and counter-clockwise directions, and in each direction it would collect and emit multiple loops. In addition, the black hole would also capture and re-transmit light from all the other stars and galaxies in the universe – including our own. (We know, contrary to Olber’s paradox, that the night sky is not totally bright, but nevertheless it is a source of considerable electromagnetic radiation.) Thus the black hole – or rather the halo surrounding the black hole – would be many times more luminous than all the stars in it’s galaxy combined, even though all this radiation would be (apparently) emitted from a very small region of space. This model can account for large variations in the luminosity very easily, since it would only require waves of in-falling material to disrupt the “3m lens” of the black hole.

There might also be other interesting effects associated with light skimming the 3m radius around a black hole. For example, the light would be heavily blue-shifted on the inward leg approaching the perihelion, and then heavily re-shifted on the outward leg, so we might expect the net result to be a minimal change in frequency relative to the original source of the light – assuming a constant radial distance between the black hole and the observer. On the other hand, if we imagine a black hole rapidly orbiting another large object (which might be a major source of light), the periodic motions of the black hole toward and away from the distant observer might result in an alternating “sling shot” effect, causing the intensity and frequency of the halo light to vary periodically. However, if some irreversibility is introduced, such as thermalization of the light during its passage near the 3m radius (possibly due to scattering or absorption and re-emission from particles of in-falling matter, or through natural approach to equilibrium of the photon gas as in cavity radiation), the out-going radiation might tend to be severely red-shifted relative to the incoming radiation.

Another, perhaps far-fetched, idea is the possibility of the circulating photons inducing stimulated emission of other photons from the excited states of the in-falling matter at the 3m radius. The physical conditions at that radius are quite similar to the conditions required to produce laser light. Recall that ordinary lasers work by bouncing an externally-supplied light back and forth through a suitably excited substance, in which the tendency for bosons to occupy the same quantum states results in “stimulated emission” of more photons, all in the same state. This stream of coherent photons then emerges as laser light. It’s interesting to consider whether, with suitable external light source and suitable in-falling material, it might be possible for “lasing” to occur near the 3m radius of a black hole. An intense source of light (perhaps from a nearby companion star) repeatedly circling a black hole through an optically excited gas of in-falling matter represents all the major ingredients of a gigantic natural laser. [After writing this I learned that, in fact, astronomers have detected evidence of natural lasing in the atmospheres of some stars.]

If black holes are fairly common, then we would expect to have observed their “3m halos”, which would be recognizable because they would exhibit incredible luminosity for their small sizes. As described above, this luminosity could easily be highly variable over short time spans, and could also be highly red-shifted, and would most likely be visible when surrounded by a galaxy of ordinary stars. Have any such objects ever been observed? Naturally we think of quasars, which are known to be extremely small objects with disproportionately high luminosity, often equally or exceeding the combined luminosity of all the stars in its surrounding galaxy, typically redshifted by large amounts, and often varying in intensity over the time span of just days or even hours.

According to the standard model of quasars, their extreme red-shift is due to the cosmological expansion of the universe. Historically there has been some controversy over the cosmological distances of quasars, but the most recent evidence seems to support the model of quasars as some kind of proto-galaxy phenomenon of the early universe. The incredible luminosity of quasars has been a challenge to explain, expecially considering that they are extremely small objects (in astronomical terms). We know quasars are small because the luminosity of some quasars is observed to change drastically on the time scale of just a single day or even less. Coherent oscillations of the energy output cannot have a period less than the difference in travel times for light from the nearest and furthest points, so the frequency of the oscillations places a limit on the possible size of the quasar.

Despite the fact that quasars are (at most) not much larger than our solar system, they must have an incredible rate of energy output in order to have their observed luminosities at cosmological distances. According to the standard model, some individual quasars emit energy at the rate of 100 large galaxies, each of which consists of billions of stars. Many attempts have been made to describe a plausible physical mechanism for emitting so much energy from such a small region. For example, there has been speculation that large amounts of matter and anti-matter may be colliding, or that millions of stars are going “super-nova” all at once. The standard model today is that the energy is most likely produced in an accretion disk surrounding a super-massive black hole. According to this model, matter is falling into a black hole whose mass is equal to a hundred million solar masses. If such a black hole consumed about 10 solar masses per year, this could account for the amount of energy released from the most energetic quasar. The variations in the brightness of quasars could be atrributed to unevenness in the rate at which material falls into the accretion disk.

However, the standard model of quasars as super-massive black holes requires us to believe that such large concentrations of matter had already formed at a very early stage in the life of the universe. It’s true that slight anisotropies in the cosmic microwave background radiation indicate that the early universe was not completely uniform, but it’s not clear that this non-uniformity would be sufficient to account for the early formation of super-massive black holes. Another questionable aspect of the standard model is its explanation for why quasars ceased to exist several billion years ago. The idea is that a super-massive black holes consume all the material within their reach, and now continue to exist at the centers of most galaxies, but, starved of in-falling matter, they do not have active accretion disks any more. This is fairly plausible as an explanation for a reduction in the number of active quasars, but since galaxies collide with each other from time to time, it’s hard to understand why there aren’t at least a few active quasars today, being fed by the billions of stars in the colliding galaxies. We can hardly argue that a few of these might go unnoticed, because a currently active quasar would be one of the most visible objects in the sky.

Considerations such as these regarding the standard explanation for the stupendous rate of energy emission of quasars have caused lingering doubts about whether quasars are actually at the cosmological distances that their redshifts suggest. If they were much closer, then the rate of energy emission needed to account for their luminosity would be greatly reduced. However, many recent observations have shown quasars embedded within active galaxies with the same redshift as the quasars, and those galaxies are known (for other reasons) to be at cosmological distances. In fact, it now appears that every quasar is situated inside a galaxy. (Early observations didn’t reveal this, because the galaxies are so faint relative to the quasars.)  So the cosmological distances, and therefore the incredibly high luminosity, of quasars seems to be well established. (It’s a happy coincidence that the most distant objects in the universe are also the most luminous, since otherwise we would never be able to see anything at such distances.) But this still leaves open the possibility that quasars are not actually sources of energy, but are merely focal points or lens, as given by the 3m halo of black holes, concentrating light from the surrounding stars.

It’s also interesting to consider the possibility of multiple black holes, perhaps orbiting each other, and the halo from each one would serve as a strong source for each of the others. If such things existed, they might be recognized by regular variations in the intensity of their combined light as they change their relative positions.

Return to MathPages Main Menu