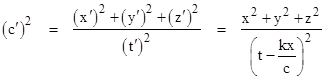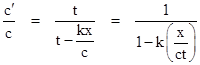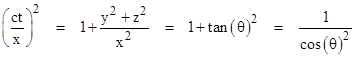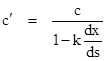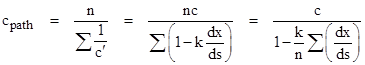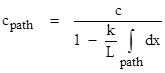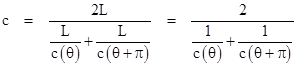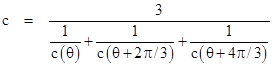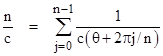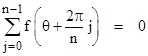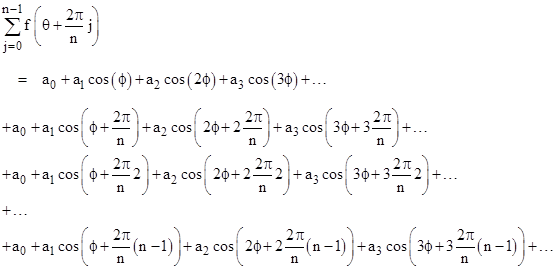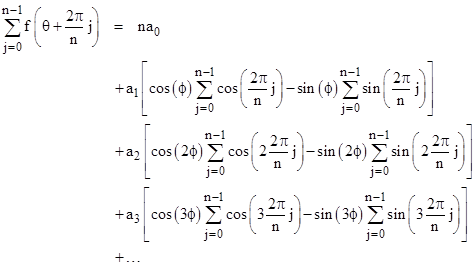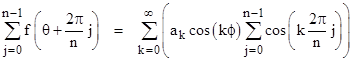Round Trips and One-Way Speeds

Given two mutually resting and unaccelerated clocks, denoted as A and B, separated by a distance L, let Clock A emit a pulse of light at time t₁, and let this pulse be reflected off clock B at time t₂ and arrive back at Clock A at time t₃. The round-trip speed of light is equal to 2L/(t₃ – t₁), but this does not tell us the one-way speed in each direction. To determine the one-way speed we need to synchronize clocks A and B, but therein lies an ambiguity, because there is more than one possible way of synchronizing two spatially separate clocks. One method is to stipulate that the pulse reflects off Clock B at the time t₂ = t₁ + (1/2)(t₃ – t₁), which is equivalent to the stipulation of isotropic light speed. In other words, with this synchronization, the speed of the pulse is the same in both directions (in terms of this coordinate system). However, nothing prevents us from defining synchronization by the more general relation

for any value of ε in the range from 0 to 1. The case ε = 1/2 corresponds to inertial coordinates, in terms of which inertia is homogeneous and isotropic, but we aren’t required to regard inertial coordinates as “true”. To this extent the choice of synchronization methods, and therefore the one-way speed of light, is conventional, in a way that the round-trip speed of light is not.

Given any inertial coordinate system x,y,z,t, we are free to apply a coordinate transformation of the form

where k = 2ε – 1. In terms of the primed coordinates the speed of light is then dependent on the angle of the light ray with respect to the x axis. For an arbitrary pulse of light emanating from the origin and reaching the point x,y,z at the time t, we have the squared speed

and in terms of the primed coordinates we have

Thus we have the ratio

Also, multiplying through equation (1) by t² and dividing by x² gives

where θ is the angle between the light ray and the positive x axis.  Hence x/(ct) = cos(θ), and we can substitute into the previous equation to give

which is the equation of an ellipse. This is the directional dependence that the anisotropic speed of light must have in order to be consistent with the primed coordinates. It corresponds to a simple tilt of the plane of simultaneity. Furthermore, this dependence is sufficient to ensure that the average speed of light over any closed loop path is precisely c (for any constant value of k in the range from −1 to +1). To prove this, we can partition any continuous path into a large number n of essentially linear segments of equal incremental length ds, so the total path length is nds. Each segment is characterized by coordinate increments dx, dy, and dz, and the cosine of the angle θ between this segment and the positive x axis is given by cos(θ) = dx/ds. Substituting into the above expression and re-arranging terms gives

so the time to traverse the segment is

The average speed over the entire path is therefore the total distance traveled, nds, divided by the sum of all the times, which gives

In the limit the summation becomes n/L times the integral of (dx/ds)ds = dx over the path, where L is the total path length, so we have

The integral vanishes for any path that begins and ends at the same x coordinate, so the average speed of light over any such path is simply c. It follows that the average speed of light over any closed loop is c.

The preceding discussion shows that an ellipsoidal dependence of light-speed on direction is sufficient to ensure the average speed c for all closed paths, but it doesn’t show necessity. We arrived at that function by considering the effect of simply shifting the simultaneity convention by tilting the locus of simultaneity. This leaves us with the question of whether any other directional dependence give invariant round-trip light speed. To prove that the ellipsoidal dependence is unique, consider the fact that, for an out and back trip along a segment of length L oriented at an angle θ (relative to the direction of maximum light speed), the round trip speed is

so it is necessary for c to be the harmonic mean of the speeds in every pair of opposite directions. This, in itself, is easy to accomplish, since we can choose the speeds arbitrarily over one hemisphere of directions, and then compute the required speeds on the remaining hemisphere accordingly. Strictly speaking, this is all we need to ensure a null result for the experiment of Michelson and Morley, because they compared the speed of light for two “back and forth” paths.

However, this is not enough to ensure the same average speed for all paths. For example, to give an average speed of c for a regular triangular path, we must have

Indeed, to ensure an average speed of c for all regular polygonal paths, we must have

for all integers n greater than 1, and for all angles θ. Since c is always positive, without loss of generality we can define a continuous function f(θ) such that

The preceding equation is satisfied if and only if

An arbitrary function f(θ) can be expressed as a cosine Fourier series as follows

so the previous summation can be written as

where ϕ = πθ/L is arbitrary. Collecting terms by coefficients, and expanding the cosines of sums, we get

Each of the sine summations vanishes identically, so we are left with

This quantity must vanish for each integer n greater than 1, and for arbitrary values of ϕ. It follows that each coefficient a_k times the corresponding inner summation must individually vanish. For k = 0 the inner summation equals n, so we must have a₀ = 0. With k = 1 the inner summation vanishes for all n greater than 1, so a₁ can be any constant. However, for k = 2 the inner summation equals 2 for n = 2. In other words, the requirement for the two-way (back and forth) average speed to be c forces a₂ = 0. Similarly for k = 3 the inner summation equals 3 for n = 3, meaning that the regular triangular path forces a₃ = 0. Likewise the requirement for the average speed of light to be c on square paths forces a₄ = 0, and so on. Thus, in order to have an average speed of c for all regular polygonal paths, it is necessary for f(θ) to be of the form a₁ cos(θ), and we have already seen that this is sufficient to give the average speed c for all closed paths.

Return to MathPages Main Menu