Translating Aristotle

Of the writings attributed to Aristotle (384-322 BC), the polished essays and dialogues which he intended for publication have been almost completely lost, with the exception of a few fragments. The great body of Aristotle's thought that has come down to us is in the form of "treatise" on various subjects, such as logic, physics, ethics, psychology, biology, and politics. It seems that these treatise began as notes on (or summaries of) Aristotle's lectures at the Lyceum in Athens. He continued to edit and revise them throughout his life, as his views evolved, but never brought them to a state of completion for publication. Subsequently they were edited and organized into "books" by his students, and then the whole corpus was transmitted through a series of transcribers, translators, and commentators.

The story of how Aristotle came to be considered the prime authority on matters of reason ("the master of those who know") is interesting. His writings certainly didn't have such a commanding status in his own time, nor at any later time in the ancient world. Even following the collapse of ancient civilization in around 500 AD, the only work of Aristotle known in the west was a Latin translation (by Boethius) of his treatise on logic. Not until the twelfth century did scholars in western Europe begin to gain access to the full range of Aristotle's treatise, and even then they did not acquire the actual Greek texts. Aristotle's teachings had survived in various scholarly communities in the east, such as among the Syrians, and these works were acquired by the Arabs when they conquered Syria around 650 AD. Eventually the works of Aristotle, along with the commentaries of Arab scholars, spread throughout the Islamic world. Beginning with the re-conquest of Toledo in 1085 and Sicily in 1091, western scholars (such as Gerard of Cremona, d. 1187) began to encounter these works and translate them into Latin. The structure of the Arab language is quite different from Greek and Latin (which are fairly similar to each other), so there was unavoidable paraphrasing in the passage from the original Greek to Arabic, and then again in the translation from Arabic to Latin. In effect, the first exposure to the full extent of Aristotle's writings came in the form of Latin paraphrases of Arab paraphrases of (and commentaries on) Syriac paraphrases of second-hand copies of the original Greek texts. Not surprisingly, the resulting Latin renderings were somewhat unreliable.

In 1204 the great Byzantine capital of Constantinople was captured by western armies during the 4th crusade, and western scholars gained access to Greek texts that were much closer to Aristotle's original writings. Around 1265, the Flemish Dominican William of Moerbeke (1215-1286) and other scholars translated these Greek texts into Latin (which can almost be done word-for-word, given the structural similarity between the two languages), and Thomas Aquinas undertook to integrate and reconcile the Aristotelian principles of reason and rational thought with Christian theology, resulting in his monumental Summa teologica. The view of Aristotle as the indisputable epitome of reason dates from this time, and held sway for about 250 years, until being superceded by the Renaissance, the Protestant Reformation, and the Scientific Revolution, each of which was, in some measure, a reaction against Aristotelian thought. As a result, today we often find Aristotle cited, especially in the sciences, as an example of erroneous thinking.

Nevertheless, the works of Aristotle are, if nothing else, a very interesting record of the attempts of one (obviously very intelligent) man to understand and systematize a wide range of knowledge on the basis of primitive principles and perceptions. For example, Books V and VI of Aristotle's Physics presents an interesting argument that space, time, and motion must all be continuous rather than discrete (atomistic). The argument relies on a number of definitions, most crucially on the definition of the word "between". This also gives a good illustration of the challenges that a scholar faces when trying to determine, first, exactly what Aristotle wrote, and second, exactly what he meant. Two of the most widely-available English translations of Aristotle's Physics are the Loeb Classic Library version by Wicksteed and Cornford (W&C), and another translation by Hardie and Gaye (H&G). Below is the renderings of Aristotle's definition of "between" contained in H&G:

That which a changing thing, if it changes continuously in a natural manner, naturally reaches before it reaches that to which it changes last, is between. Thus 'between' implies the presence of at least three things: for in a process of change it is the contrary that is 'last': and a thing is moved continuously if it leaves no gap or only the smallest possible gap in the material-not in the time (for a gap in the time does not prevent things having a 'between', while, on the other hand, there is nothing to prevent the highest note sounding immediately after the lowest) but in the material in which the motion takes place. This is manifestly true not only in local changes but in every other kind as well. (Now every change implies a pair of opposites, and opposites may be either contraries or contradictories; since then contradiction admits of no mean term, it is obvious that 'between' must imply a pair of contraries) That is locally contrary which is most distant in a straight line: for the shortest line is definitely limited, and that which is definitely limited constitutes a measure.

Compare this with the same passage in the W&C translation:

Since all change is between opposites, and opposites are either contraries or contradictories, and there is nothing between contradictories, it is clear that the intermediate or "between" can only exist when there are two contraries.  B is between A and C if anything passing (locally or otherwise) by a continuous change in accordance with its nature must necessarily come to B before it reaches the extreme C on its way thereto from A.  'Between' implies at least three terms: the 'whence' of the passing, the opposite of the whence, namely the 'whither', and something on the line of passage, nearer to the whence than the whither is; and the passage is continuous if there is no break or leap in the course - or, if any, only the minimum.  I am speaking of a break, not in time, but in that with respect to which the changing thing is changing; for in time the bottom note of the diapason may be followed by the top note (which constitutes the maximum possible break or leap in the scale) just as immediately as any two notes severed by the smallest conceivable interval.  All which applies not only to changes of place but the other kinds of change as well.  In the local application of the word, one thing is the contrary of another, if it is farther from it, in a straight line, than any other individual thing of the same order in the field under consideration.  The straight line is chosen because, as the shortest, it is the only definite one between any two positions, and a measure or standard must be definite.

Notice that the first sentence in W&C ("Since all change is between opposites...") does not appear in the R&H translation until near the end, and then only parenthetically ("Now every change implies a pair of opposites..."). Also, W&C avail themselves of symbolic characters A, B, C, whereas these do not appear at all R&H's strictly verbal rendering. Throughout there are major differences in syntax, sentence structure, and vocabulary. This shows why we should always be cautious when quoting "what Aristotle said". Obviously it's not possible to directly transliterate from the ancient Greek to modern English, so at best a translator can only hope to convey the correct sense of what Aristotle was trying to say.

In that regard, the definition of "between" given in both of the above translations has several aspects that seem questionable. This definition occurs in a sequence of definitions covering, in order, the terms together, apart, touching, between, next in succession, contiguous, and continuous. One puzzling aspects of the definition of 'between' is that it invokes the word "continuous" even though the definition of continuous is not given until later. Furthermore, the definition of "between" (as rendered in these translations) is based explicitly on a continuous passage, and yet it includes the additional remark describing when "the passage" can be considered continuous. Also, even if we take just the first part of this clause, which asserts that the passage is continuous "if there is no break or leap in the course", it is not the same as Aristotle's subsequent definition. Moreover, the reference to "the smallest possible gap" ("no break.... or, if any, only the minimum"), taken at face value, seem to flatly contradict the notion of continuous change as subsequently defined. W&C even note that "the meaning of the qualification 'only the minimum' has perplexed commentators".

It seems to me that the word used or intended by Aristotle in his definition of "between" was not really "continuous" (συνεχεζ) in the sense of the subsequent definition, but was actually something like the word "continuing" (συνεχϖζ). This interpretation not only avoids the out-of-sequence appearance of the technical term "continuous", it also fits with the overall sense of the definition of 'between', because, after all, the quality of betweenness applies to a sequence of discrete atoms just as well as it does to the points of a line. Aristotle was clearly presenting a general definition of the concept "between", so it would not have made sense for him to restrict the definition to continuous sequences. Furthermore, if we allow this definition to apply to discrete as well as continuous sequences, then the sense of the phrase "no break.. or, if any, only the minimum" becomes clear. Aristotle had in mind the continuing sequence of integers (for example), and the number 7 is between 3 and 12 because it is necessarily encountered when passing without a break or jump, i.e., with only the minimum steps, from 4 to 12. If we passed by taking steps of size 2, we would not encounter the number 7 during the passage.

Moreover, only on the assumption that Aristotle meant "continuing" rather than "continuous" in his definition of "between" can we make sense of the rest of Books V and VI, in which he labors to demonstrate that space, time, and motion are necessarily continuous. If, as is traditional, we interpret Aristotle's definition of "between" as involving necessarily continuous passages, then he has essentially just defined motion (and therefore space and time) to be continuous, and his subsequent detailed demonstration of their continuity is both circular and superfluous (a charge that has indeed been leveled against it by critics). The fact that the crucial Greek word used in the definition of "between" is  συνεχϖζ  rather than  συνεχεζ  seems to support the idea that Aristotle did not intend the former to be understood as "continuous" in the same sense as the latter.

On the basis of this more plausible definition of "between", we can re-evaluate Aristotle's argument for the continuity of space, time, and motion. The basic premise of the argument is that the set of possible spatial locations consists of a single totally-ordered sequence, and likewise the sequence of temporal instants is totally-ordered. (He says in Book IV that "the same time is everywhere simultaneously".) Notice that the sequences of locations and times are not assumed to be continuous. It is, however, assumed that an object must encounter every location that exists between two locations as it passes from one to the other, and likewise for instants of time. In other words, an object cannot "skip" locations or instants, because by its nature it must continually (not necessarily continuously) exist.

Now Aristotle posits the existence of a possible state of objects called local motion, which consists of a state of transition of a given object from one spatial location to another, and this change in location corresponds to a change in time. (In fact, Aristotle often seems to suggest that time is nothing other than a measure of change.) Local motion is actually one of three types of change that Aristotle recognizes, the other two between changes in quality and changes in quantity. He asserts that change exists only between contraries, which are defined in the case of local motion as the extreme limits of a class of entities along a straight line.

One location is the contrary of another if it is farther from it, in a straight line, than any other individual thing of the same order in the field under consideration.  The straight line is chosen because, as the shortest, it is the only definite one between any two locations.

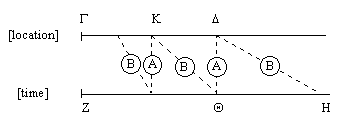
Aristotle then makes the further supposition that an object cannot be both in motion to (or from) a location and in that location. "For instance, a man who is walking to Thebes cannot have already got to Thebes and be there at the same time...". From these premises, Aristotle claims that the continuity of space, time, and motion necessary follows, and he gives several illustrations of this in Book VI. One of the most interesting is in Chapter II (232b,25), which is illustrated by means of two parallel line, one representing spatial location and the other representing time, as shown below.

Let A and B denote particles moving from the location Γ to the location Δ, and suppose B is moving more slowly than A (which is to say, B moves a lesser distance in any given time, and A arrives at any given location in less time). It follows that the arrival of B at the location Δ will correspond to a time H that is strictly greater than the time Θ when A arrives at Δ. Hence there exists an instant Θ between Z and H, and from the definition of "between", and the postulate that an object cannot skip locations or instants, it follows that particle B, in passing from Z to H, must also exist at the instant Θ. However, since B is the slower of the two particles, its spatial location corresponding to that instant must be a point K between Γ and Δ. But this, in turn, implies that the particle A must encounter the location K while passing from Γ to Δ. Obviously this chain of implication continues indefinitely, from which Aristotle infers that there cannot be any smallest interval of space or time, that these sequences are therefore infinitely divisible (and hence continuous according to Aristotle's conception), and the continuities of space, time, and motion are all inextricably linked.

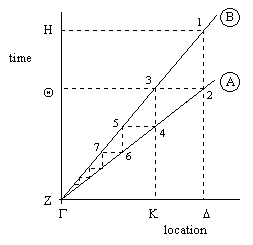
Each dashed line marked with a circled "A" or "B" on the diagram represents a correspondence between a spatial location and a time, signifying the spacetime position of the respective particle. Since any location can be associated with any time, Aristotle (or is later illustrators) might have considered the alternative of drawing the two axes perpendicular to each other, in which case each dashed line on the original figure is represented by a single point, and the locus of all the points of a (uniformly moving) particle's position is a straight line, as shown below.

The chain of implication in Aristotle's argument proceeds through the infinite sequence of spacetime events marked 1,2,3,... Of course, from the modern point of view, the property that there exists another element between any two given elements does not imply a continuum. That property is called denseness. For example, the set of rational numbers has this property (between any two distinct rationals there is another rational), but they do not constitute a continuum, because there are real number that are not rational. (It's slightly surprising that Aristotle didn't take this into consideration, since he was well aware of the existence of irrational numbers.)

On the other hand, Aristotle's thesis that space and time are essentially a single continuum is a strikingly modern concept (despite his insistence on the uniqueness of the temporal foliation, i.e., his belief that "time is identical everywhere simultaneously").

Return to MathPages Main Menu