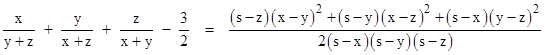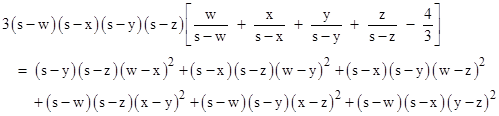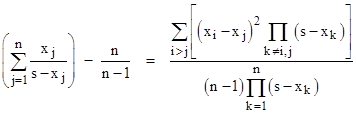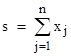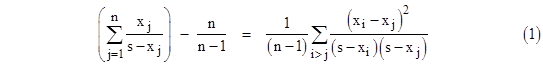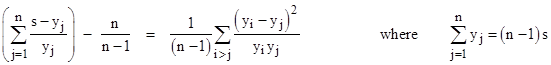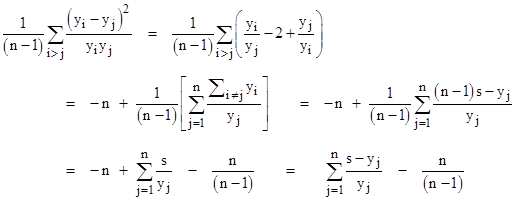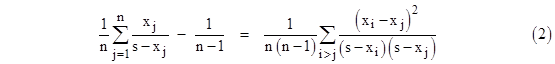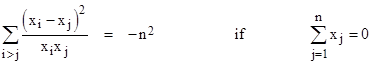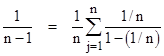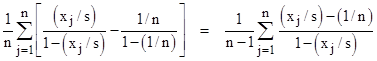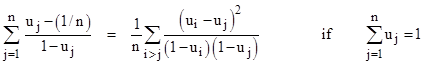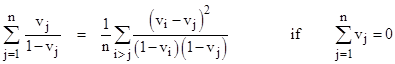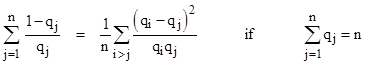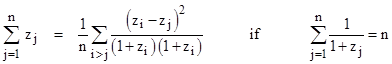Proving Algebraic Inequalities

If x and y are positive real numbers then clearly the sum x/y + y/x is greater than or equal to 2, because the quantity x/y + y/x – 2 can be multiplied through by xy (which is positive if x and y are both positive) to give x² + y² – 2xy, which can also be written as (x–y)². Since the square of a real number is always non-negative, this proves that x/y + y/x is never less than 2. Of course this proof is also valid if x and y are both negative real numbers, but not if one is positive and the other negative, because in that case the inequality is reversed when we multiply by xy.

Now suppose we want to prove the slightly more complicated inequality

for any positive real values of x, y, and z. There are several ways we could approach this. For example, if we define s = x + y + z then the quantity on the left hand side can be written as

Dividing all the numerators and denominators by s, and defining the positive variables X = x/s, Y = y/s, and Z = z/s, we have

We note that X + Y + Z = 1, and each of the numbers X,Y,Z is less than 1. Hence each term is a convergent geometric series, e.g., the first term equals the infinite sum X + X² + X³ + ... Combining terms of equal powers gives

The first quantity in parentheses is equal to 1, whereas the remaining terms vary depending on the partition of 1 into the three positive summands X, Y, and Z. It's intuitively obvious that each sum of powers is minimized by the equal partition, i.e., by setting X = Y = Z = 1/3. To show this rigorously, we can substitute 1–X–Y in place of Z and then set the partial derivatives of the general sum of powers with respect to X and Y equal to 0. The derivative with respect to X gives

which implies X = 1–X–Y = Z. Likewise the derivative with respect to Y implies Y = Z, and hence X = Y = Z = 1/3. Substituting 1/3 for X, Y, and Z into the prior expression gives 3/2 for the minimum possible value, which is achieved when, and only when, x = y = z.

This gives a reasonably straightforward proof, which immediately generalizes to the case of n variables. For example, we have

for four positive real variables. In general for n variables the sum is no less than n/(n-1). However, the above proof makes use of infinite series and calculus, whereas in the case of just two variables the inequality x/y + y/x ³ 2 was seen to be due to the simple algebraic fact that (x–y)² cannot be negative. It's tempting to think that every simple algebraic inequality – at least those that permit equality – must be expressible in the form of an algebraic square (or positively-weighted sum of squares) being non-negative.

Notice that in the case of two variables we had equality x/y + y/x = 2 if and only if x = y, which is consistent with the fact that the quantity (x–y)² vanishes if and only if x = y. Similarly in the case of three variables we have equality if and only if x = y = z, and this suggests that if we are to express the inequality in terms of a square (or sum of squares) being non-negative, the quantities to be squared must vanish when x = y = z. Hence we expect the solution must involve the quantities (x–y), (x–z), and (y–z). Now, the sum of the squares of these quantities is not a factor of the desired inequality, but the vanishing of the sum of squares of those three differences is equivalent to the vanishing of the sum of squares of any two of them (by transitivity). Hence to give the correct degree and maintain symmetry we are led to the desired algebraic identity

where s = x + y + z. Since x,y,z are positive, this quantity is necessarily non-negative, and vanishes if and only if x = y = z. It’s interesting to apply this formula to triangles with edge lengths x, y, z, considering that the denominator of the right hand side is 2/s times the square of the area of the triangle (by Heron’s formula).

Similarly the inequality for four variables is made manifest by the algebraic relation

where s = w + x + y + z. In general, any n variables x₁, x₂, …, x_n satisfy the following algebraic identity that makes the desired function equal to a positively-weighted sum of squares:

where

From this general form it’s easy to see that the most natural expression is to carry out the division on the right side, leading to the nice identity

Thus the left hand side is a simply-weighted sum of the squares of the n(n–1)/2 pairwise differences between the n basic quantities. This makes the general inequality self-evident, and this form also clarifies how the identity applies in the case n = 2. (It’s worth noting that although this proves the family of inequalities for real-valued variables, it does not for complex variables, because in that case the square of a number need not be positive.) To prove this identity, it’s convenient to define the variables y_j = s – x_j, in terms of which the relation is

The right-hand side of the equation can be written in the form

which equals the left hand side of the identity.

Incidentally, if we divide (1) through by n we get

which shows that the average of the original ratios minus 1/(n–1) equals half the average of the weighted squared differences. If the sum s of the x parameters is zero, the identity reduces to

On the other hand, if s is not zero, we can normalize all the x parameters so that s = 1. Also, we can further simplify (2) by noting that

Thus we can bring the constant term inside the summation, allowing us to write the left side of (2) as

Therefore, in terms of the normalized parameters u_j = x_j/s, we can re-write the identity (2) in the form

If we further normalize the parameters by defining

the identity takes the form

Alternatively, in terms of the parameters q_j = 1 – v_j, we have

Finally, if we define parameters z_j related to q_j by

then the identity takes the form

Return to MathPages Main Menu