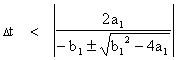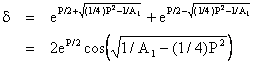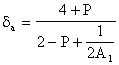|
3.3 Modified Methods for Second-Order Interpolation |
|
|
|
3.3.1 Cascaded First-Order Simulation |
|
|
|
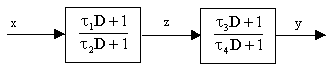
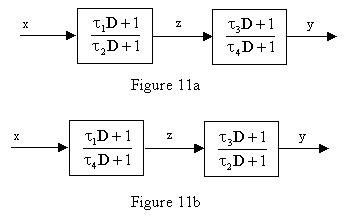
In Section 3.1 we briefly considered the use of two first-order simulations in series as a means of representing second-order response. This section presents a more detailed analysis of such a configuration as illustrated in the figure below. |
|
|
|
|
|
Figure 10 |
|
|
|
By equation (2.2.2-1) we have |
|
|
|
|
|
|
|
where |
|
|
|
|
|
The functions f1, f2, f3 can be any set of first-order coefficient functions as defined in Section 2.2 (e.g., equation 2.2.3-3). Our objective is to derive a single recurrence formula in terms of yn and xn only, so we must eliminate the intermediate variable zn. Substituting the expression for zi from equation (3.3.1-1) into equation (3.3.1-2), we have |
|
|
|
|
|
|
|
The formula still has a term involving zi-1, since it’s impossible to eliminate both zi and |
|
zi-1 from equations (3.3.1-1) and (3.3.1-2) simultaneously. Therefore, we consider the relations from the previous iteration |
|
|
|
|
|
|
|
Eliminating zi-2 from these equations and solving for zi-1 gives |
|
|
|
|
|
|
|
Substituting this expression for zi-1 into equation (3.3.1-3) gives the desired recurrence formula for two first-order lead/lag functions in series: |
|
|
|
|
|
|
|
where |
|
|
|
|
|
Recalling that the sum of the F functions is 1, as is the sum of the G functions, it is easily verified that the sum of c1 through c5 from the preceding equations is also 1, as required. |
|
|
|
Assuming constant t, the optimum equations for the F and G functions are given beneath equation (2.2.3-3), and on this basis (comparing the expressions for t1 and t4 developed in Section 3.1 with the definitions of r1 and r2 given beneath (3.2.3-4), and noting that t2 r2 = t4 r4 = -1) we can write |
|
|
|
|
|
|
|
Therefore, the first two coefficients of equation (3.3.1-4) are given by |
|
|
|
|
|
|
|
These are just –g and d respectively, so if we convert equation (3.3.1-4) to the form of equation (3.2.2-3) we have |
|
|
|
|
|
|
|
Also, since c3 + c4 + c5 = 1 – c1 – c2, we have |
|
|
|
|
|
|
|
To determine L4, recall that L4 = c4 + 2c5. Substituting the expressions from equations (3.3.1-5) we have |
|
|
|
|
|
|
|
Substituting the appropriate expressions for the F and G functions from the definitions beneath equation (2.2.3-3) gives |
|
|
|
|
|
|
|
Since r1 = -1/t4 and r2 = -1/t2, we can simplify this equation to arrive at |
|
|
|
|
|
|
|
Furthermore, since t1 + t3 = b2 and t2 + t4 = b1 (as shown in Section 3.1), this can be written as |
|
|
|
|
|
|
|
which is identical to equation (3.2.3-8). Thus we’ve shown that two first-order simulations in series are functionally equivalent to the optimum second-order recurrence formula when DDxi is zero (i.e., when the xn samples are linear with time), assuming that the optimum recurrence coefficients are used in the first-order algorithms. It follows that the recurrence formula for two optimum first-order algorithms in series can be written in the “standard form” of equation (3.2.5-2) where the coefficients A, B, and C are just as given by equations (3.2.5-3). However, the D coefficient in this case is given by F3G3. Substituting the optimum first-order coefficient formulas from beneath equation (2.2.3-3) for F3 and G3, we have |
|
|
|
|
|
|
|
which can be written |
|
|
|
|
|
(3.3.1-6) |
|
|
|
Since this is not equivalent to either (3.2.5-4) or (3.2.5-5), it’s clear that two optimum first-order functions in series do not reproduce the exact second-order response corresponding to either point-to-point or second-order interpolation of the input x(t). In fact, the D coefficient given by (3.3.1-6) can be complex, which is never the case with either point-to-point or second-order interpolation. |
|
|
|
The conditions under which D is non-real are clarified by re-writing equation (3.3.1-6) in the form |
|
|
|
|
|
|
|
where d1 = b12 – 4a1 and d2 = b22 – 4a2. This shows that D is real if and only if the product of d1 and d2 is a positive real number, i.e., if d1 and d2 are both real and of the same sign, or are complex conjugates with a positive product. It is interesting that if both d1 and d2 are real and negative, meaning that the combined function is under-damped in both directions, then the discrete-time response of two conjugate first-order functions in series can still be reproduced using the second-order recurrence formula (3.2.5-2) with purely real coefficients, even though all the t in the first-order functions are complex. |
|
|
|
Also, since equation (3.3.1-6) is not invariant under an exchange of t1 and t4, or an exchange of t1 and t3, it follows that the two sets of cascaded functions shown in Figure 11 are not functionally equivalent when implemented in discrete time, even though they are equivalent in the continuous domain. |
|
|
|
|
|
|
|
In the preceding discussion it was assumed that the individual first-order algorithms using the optimum recurrence coefficients (for constant t), but equation (3.3.1-4) is applicable to the cascading of any first-order recurrence algorithm that can be expressed in the form of equation (2.2.2-1). |
|
|
|
|
|
3.3.2 Finite Difference Method |
|
|
|
The most direct approach to simulating a differential equation such as |
|
|
|
|
|
|
|
is by substitution of simple finite difference ratios for the differentials. The derivative of y(t) at ti-1 is approximately equal to the average of the “slopes” on the two neighboring intervals |
|
|
|
|
|
and we can approximate the second derivative of y(t) at ti-1 by the change in “slope” per interval |
|
|
|
|
|
|
|
Similarly for the function x(t) we have the approximations |
|
|
|
|
|
|
|
|
|
|
|
Substituting from equations (3.3.2-2) through (3.3.2-5) into equation (3.3.2-1) for the time ti-1, and solving for yi gives the recurrence formula |
|
|
|
|
|
|
|
where |
|
|
|
|
|
The relation between this approximate solution and the optimum solution derived in Section 3.2 is clarified by comparing equations (3.3.2-4) and (3.3.2-5) with the coefficients of equation (3.2.3-1). This comparison shows that equations (3.3.2-4) and (3.3.2-5) are optimum if (but not only if) we assume the function x(t) is the second-degree polynomial through xi-2, xi-1, and xi, just as was assumed in the derivation of the optimum solution. Similarly, equations (3.3.2-2) and (3.3.2-3) are optimum if we assume the function y(t) is the second-degree polynomial through yi-2, yi-1, and yi. However, the simultaneous imposition of both these assumptions is inconsistent with equation (2.2.3-4), since it was demonstrated in Section 3.2 that if x(t) is a second-degree polynomial then y(t) is not. Hence, the finite difference method is intrinsically inexact, except in the limit as Dt goes to zero. |
|
|
|
|
|
3.3.3 Bilinear Substitution Algorithm |
|
|
|
Another method for deriving a recurrence formula to simulate a given continuous response is the bilinear substitution algorithm (also known as Tustin’s algorithm). This method was mentioned briefly in Section 2.3.2 as it applies to first-order transfer functions, where it was shown to be equivalent to the substitution of simple finite difference ratios. When applied to other transfer functions, however, the bilinear substitution algorithm is not generally equivalent to the method of finite differences. In this section we present a more detailed examination of the bilinear substitution method and its underlying assumptions. |
|
|
|
To apply the bilinear substitution algorithm, the basic governing equation is written using the differential operator D. For the general second-order lead//lag equation we have |
|
|
|
|
|
|
|
Then according to the algorithm we make the substitution |
|
|
|
|
|
|
|
where the symbol z-1 represents the “past value” operator (also known as the “time delay” operator). In general, z-m xn = xn-m. Substituting equation (3.3.3-2) into equation (3.3.3-1) gives |
|
|
|
|
|
|
|
Multiplying through by Dt2 (1 + z-1)2 we have |
|
|
|
|
|
|
|
Combining terms by powers of z gives |
|
|
|
|
|
|
|
Carrying out the past value operations and solving for yi gives the general second-order recurrence formula based on bilinear substitution: |
|
|
|
|
|
|
|
where |
|
|
|
|
|
Comparing these coefficients with those of equation (3.3.2-6) shows that the methods of finite differences and bilinear substitution are identical to the first order in Dt, but differ in terms of Dt2. (Of course, both methods converge on the exact solution in the limit as Dt goes to zero.) |
|
|
|
The use of a “recipe” such as bilinear substitution to derive recurrence formulas is convenient, but it tends to obscure the basic assumptions implicit in the method. To illuminate these assumptions, we now give another, more explicit, derivation of equation (3.3.3-4). To derive a recurrence formula for simulating equation (3.3.2-1), write the equation in specific form for three consecutive instants. (In general, to derive a recurrence for a differential equation of order N, write the specific equation for N+1 consecutive instants.) Using dot notation for time derivatives we have |
|
|
|
|
|
|
|
We then sum each pair of consecutive equations to give |
|
|
|
|
|
|
|
|
|
|
|
These two equations are exact, but we now introduce an approximation by assuming that the change in any variable during any interval Dt is given by trapezoidal integration of its derivative during that interval. In the present example we will need the following “integrations”: |
|
|
|
|
|
|
|
for all n. Rearranging, we have |
|
|
|
|
|
|
|
Substituting these expressions into equations (3.3.3-5) and (3.3.3-6) gives |
|
|
|
|
|
|
|
and |
|
|
|
|
|
Adding these two equations gives the single equation |
|
|
|
|
|
|
|
Substituting from equations (3.3.3-8) (taking the differences of the first derivatives on successive indices to give expressions for the differences in derivatives at the times ti and ti-2), we can eliminate the “dotted” terms, and then multiplying through by Dt2, the result is identical to equation (3.3.3-3), which leads to the recurrence formula (3.3.3-4) which was derived using the bilinear substitution recipe. |
|
|
|
The integrations expressed
by equations (3.3.3-7) treat each of the functions |
|
|
|
Perhaps for historical reasons, the approach of bilinear substitution is in accord with the techniques of analog simulation, where differential equations are commonly treated in integral form. For example, if we integrate equation (3.3.2-1) twice with respect to time, we have |
|
|
|
|
|
|
|
Naturally, direct application of trapezoidal integration to this equation leads to exactly the same recurrence formula as is given by bilinear substitution. |
|
|
|
|
|
3.3.4 Simplifications Based on Approximations of ez |
|
|
|
In this section we return to the optimum recurrence formula presented in Section 3.2.3 to show how it may be simplified by substituting approximations for ez into the coefficient expressions. First, substituting the lowest-order Taylor series approximation of ez |
|
|
|
|
|
|
|
into the equation for g in Table 2 gives |
|
|
|
|
|
|
|
Using the subscript “a” to denote approximate values, this equation can be written |
|
|
|
|
|
|
|
By equations for r1 and r2 beneath (3.2.3-4) we have |
|
|
|
|
|
|
|
so equation (3.3.4-2) becomes |
|
|
|
|
|
|
|
Similarly, da can be determined by using equation (3.3.4-1) to approximate the exponentials in equation for d in Table 2, which gives |
|
|
|
|
|
|
|
Inserting these approximate expressions for g and d along with the exact expressions for a and b into the coefficients of equation (3.2.3-7), we arrive at the general recurrence formula |
|
|
|
|
|
|
|
where |
|
|
|
|
|
Since this recurrence formula is based on the exponential approximation given by equation (3.3.4-1), it will give acceptable results only if the exponents r1Dt and r2Dt are very much smaller than 1, which means that the execution frequency must be very high. |
|
|
|
Rather than proceeding to higher-order Taylor series approximations, we will turn to a more efficient approximation of the exponential |
|
|
|
|
|
|
|
Substituting this into equations for g and d in Table 2 gives the approximate parameters |
|
|
|
|
|
|
|
These are exactly the same approximations as were derived using bilinear substitution in Section 3.3.3. The homogeneous (i.e., unforced) response is fully determined by these two coefficients. In general, the substitution of (3.3.4-3) into the analytical expression for the exact Nth-order homogeneous response leads to the same recurrence coefficients (for the output variable terms) as does bilinear substitution. (Recall from Section 2.3.2 that the total solutions match in the case of first order response.) This clarifies the correspondence between bilinear substitution and the optimum solution, and provides an alternative derivation without resort to trapezoidal integration. (The coefficients for the input variable terms can be derived similarly by substituting (3.3.4-3) into the “homogeneous form” of x(t), as if it were the output of the transfer function, and then applying the appropriate scale factor.) |
|
|
|
|
|
3.3.5 Discussion |
|
|
|
The derivations in the preceding sections have assumed that the coefficients of the second-order differential equation to be simulated were constant. In the case of constant coefficients there is little reason to use an approximate method to determine the corresponding recurrence coefficients, since they can be pre-computed (offline) using the optimum solution. However, in practice the coefficients are often not constant. Even assuming the “variable t” response can be approached using the “constant t” solution with a sufficiently small Dt, variable coefficients make it necessary for the recurrence coefficients to be periodically recomputed. Approximate methods such as those presented above are used to minimize the computational burden. |
|
|
|
We saw in Section 3.3.1 that cascaded first-order algorithms with real coefficients cannot be used to simulate all possible second-order response. Therefore, in this discussion we will focus on the three general approximate methods described above (1) finite differences, (2) Taylor’s series substitution, and (3) bilinear substitution. Our assessment of these three methods will be based on the fact that each of the corresponding recurrence formulas is given by (3.2.3-7) with an appropriate choice of approximations for the parameters g and d. This was proven in Section 3.3.3 for the methods of Taylor series and bilinear substitution. Furthermore, it can easily be verified that if g and d are approximated by |
|
|
|
|
|
|
|
then equations for the coefficients of (3.2.3-7) give the recurrence coefficients for the method of finite differences. This value of ga follows from the exponential approximation |
|
|
|
|
|
|
|
which is the same approximation as equation (3.3.4-3). However, in this case it is applied to the combined exponential (r1 + r2)Dt instead of the individual exponentials r1Dt and r2 Dt as was done to yield the bilinear substitution recurrence. The approximation for d in the case of finite differences does not correspond exactly to any well-defined exponential approximation. It is consistent with the assumption |
|
|
|
|
|
|
|
If r1 = r2 = r this is equivalent to the approximation ex » (2-x2)/(2-2x), which for small values of x is better than the first-order Taylor series approximation, but not as good as either the second-order Taylor series or the (3.3.4-3) approximation. |
|
|
|
We will assess the three approximate methods by comparing their respective expressions for ga and da with the optimum expressions for g and d. For this purpose we define the dimensionless parameters |
|
|
|
|
|
|
|
In these terms the values of g and ga for the various methods can be summarized as follows: |
|
|
|
Optimum: |
|
|
|
First-Order Taylor Series: |
|
|
|
Bilinear Substitution: |
|
|
|
Finite Differences: |
|
|
|
These expressions show that in order to give reasonably accurate values of g the Taylor series and bilinear substitution methods must satisfy two requirements, namely, P must be small and A1 must be large. If, for example, we require P < 1 and A1 > 1, then we have the following limitations on Dt |
|
|
|
|
|
|
|
In contrast, the method of finite differences only needs to satisfy the first of these requirements. Another derivation of these two limits is to recognize that the exponential approximations are valid only for exponents that are small relative to 1. Therefore, we require |r1,2 Dt| < 1. This implies that |
|
|
|
|
|
|
|
If b1 is much
larger than a1, this reduces to Dt < |a1/b1|
, whereas if a1 is much larger than b1 this reduces to |
|
|
|
Equations (3.3.5-1) and (3.3.5-2) also show that bilinear substitution will give a slightly more accurate ga than finite differencing when a1 is positive, but slightly less accurate when a1 is negative. This is because for a wide range of positive A1 values the inverse A1 terms in (3.3.5-1) actually improve the exponential approximation, but if A1 is negative these terms make the approximation worse. |
|
|
|
The expressions for d and da for the various methods are as follows: |
|
|
|
Optimum: |
|
|
|
Taylor Series: |
|
|
|
Bilinear Substitution: |
|
|
|
Finite Differences: |
|
|
|
By plotting d and da versus
P for various values of A1 it can be shown that the relative
accuracies and limitations on Dt are essentially the same as
for the parameter g. The major difference is that the limitation |
|
|
|
The limitations on Dt imposed by the use of approximate recurrence coefficients are in addition to, and independent of, the requirements imposed by the intrinsic information rates of the input and output signals. To illustrate this fact, consider the dynamic function represented by the equation |
|
|
|
|
|
|
|
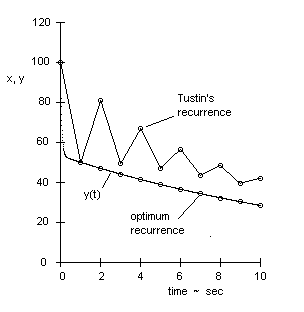
with the initial conditions y(0)=100 and y(1) = 50. Since the input signal is always zero, the recurrence formula given by equation (3.2.2-1) is just |
|
|
|
yi = (c1) yi-2 + (c2) yi-1 |
|
|
|
Also, since x(t) is constant, and the natural frequency of the response is only 0.16 cycles per second, it is clear that the intrinsic information flow rate of this system can be adequately represented with a sampling frequency of 1 sec-1, which corresponds to a discrete time interval of Dt = 1 second. On this basis, the equations for c1 and c2 beneath (3.2.3-7) give the optimum recurrence formula. |
|
|
|
yi = (-1.125352E-7) yi-2 + (0.939182) yi-1 |
|
|
|
In contrast, the method of bilinear substitution gives the formula |
|
|
|
yi = (0.729730) yi-2 + (0.162162) yi-1 |
|
|
|
The computed response given by these two formulas is plotted in Figure 12, superimposed on the exact analytical solution. |
|
|
|
|
|
Figure 12 |
|
|
|
Clearly the formula based
on bilinear substitution does not adequately represent the system under these
conditions. This is because when using bilinear substitution (or any of the
other approximate methods discussed in this document) the execution period must
not only be small enough to resolve the input and output signals, it must
also satisfy the requirements Dt < |a1/b1|
and |
|
|
|
In the present example we have a1=1 and b1=16, so the execution interval must be less than 0.0625 sec when using an approximate method. Thus the execution frequency in this example must be 16 times greater when using the approximate recurrence formula than when using the optimum recurrence formula. |
|
|
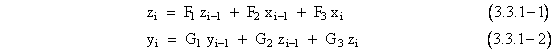

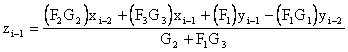
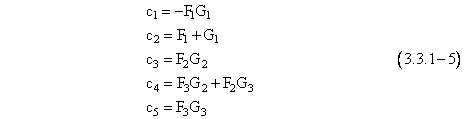
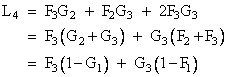
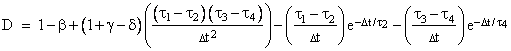
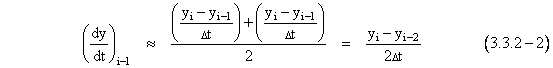
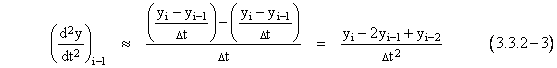
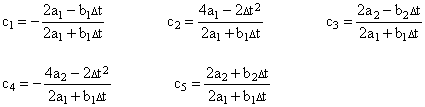
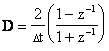 (3.3.3-2)
(3.3.3-2)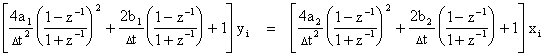


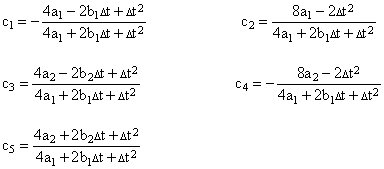
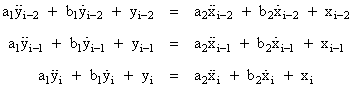
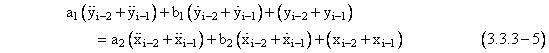
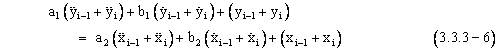
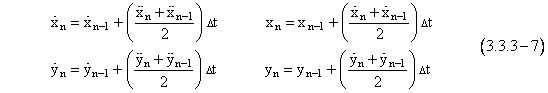
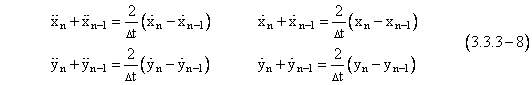
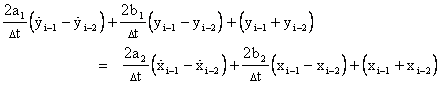
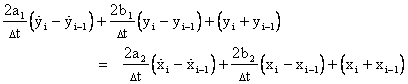
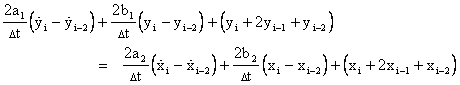

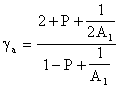 (3.3.5-1)
(3.3.5-1)