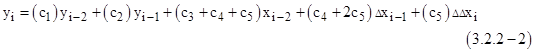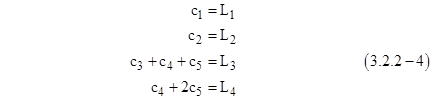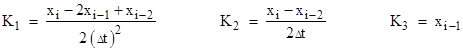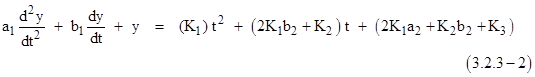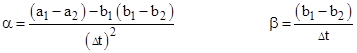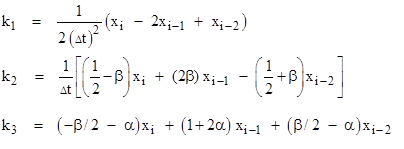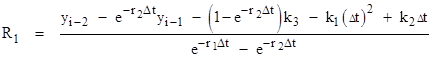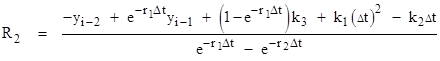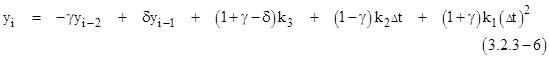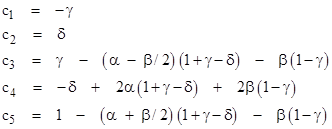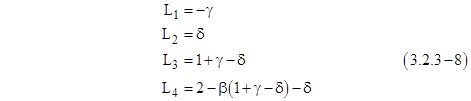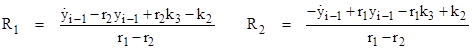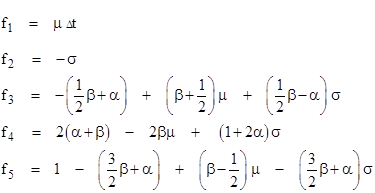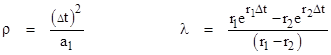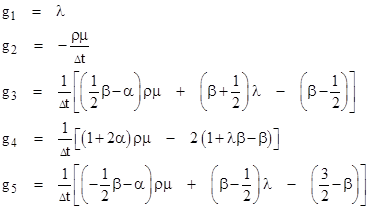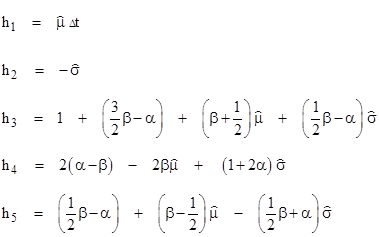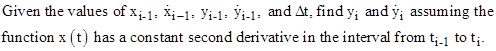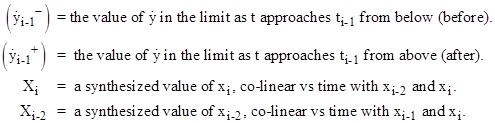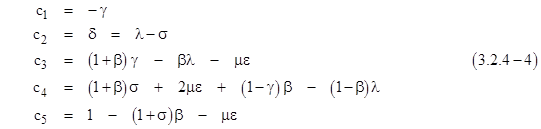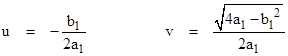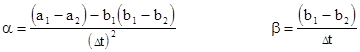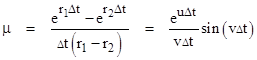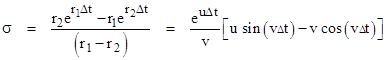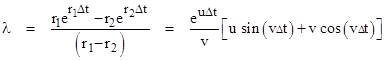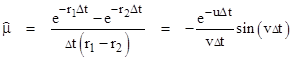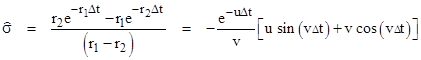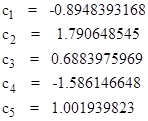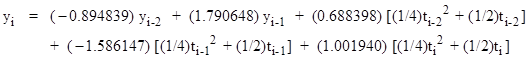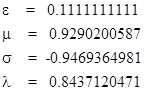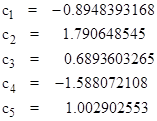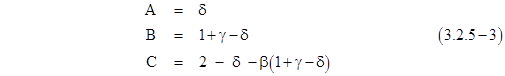3.2  Optimum Second Order Recurrence Formulas

3.2.1  Basic Assumptions

It was convenient in the treatment of first order simulation to employ a simple mnemonic subscripting scheme, using p and c to denote “past” and “current” values of the time dependent variables. However, when dealing with higher order response the basic recurrence formulas normally involve more than two time states, and it is expedient to adopt a more general notation. We will represent any time dependent variable q by an ordered sequence of discrete values

where each of these discrete values is understood to be the true value (or at least the best available estimate) of the variable q at the times

respectively. These values of time form an ordered sequence such that for all n

where Δt is defined as the execution period of the simulation. By convention, the subscript “i” denotes the “current value”, and variables subscripted with i–1, i–2, and so on are referred to as “past values”. The subscript n is used to denote the general term of the sequence.

For purposes of a simulation algorithm, it is assumed that all values of the input sequence x_n are known up to and including the current value x_i. It is also assumed that all values of the output sequence y_n are known up to but not including the current value y_i. The specific task of a second-order simulation is to compute y_i given that the continuous variables x and y are related according to equation (3.1-1). For real-time simulations, we will assume that the time required for the computation is negligible relative to the sampling interval Δt.

Even though all past values of x and y are theoretically known, a practical algorithm will retain only a limited number of them. To determine how many past values are necessary, we note that equation (3.1-1) includes the second derivative of x, and that a minimum of three values are required to provide an estimate of the second derivative of a function. Therefore, in addition to x_i, the algorithm must have access to the past values x_i-1 and x_i-2. Equation (3.1-1) also includes the second derivative of y, so we anticipate that two conditions on y must be specified to determine the solution. For this purpose we will use the past values y_i-1 and y_i-2.

The solution of equation (3.1-1) requires a continuous definition of x(t), so the algorithm must interpolate between the three available discrete values. However, unlike the first-order case, the optimum interpolation here is not obvious. Since three points can only provide a single estimate of the second derivative, it might seem reasonable to assume a function x(t) with a single, constant, second derivative during the double interval from x_i-2 to x_i. This would imply that x(t) can be represented by a second-degree polynomial passing through the three given values of x.

However, there are two possible objections to this approach. First, it introduces an inconsistency of interpolation on successive executions of the algorithm. For example, when y_i is being computed, the input function between t_i-2 and t_i is assumed to be the second-degree polynomial that passes through x_i-2, x_i-1 and x_i. But on the next pass, when y_i+1 is being calculated, the input function between t_i-1 and t_i+1 is assumed to be the second-degree polynomial that passes through x_i-1, x_i, and x_i+1. Hence the function between t_i-1 and t_i has been represented by two different polynomials on successive passes.

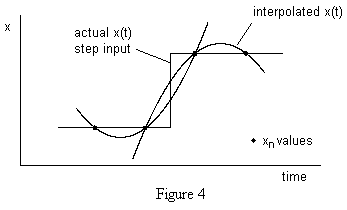
The other possible objection to the use of second order interpolation concerns the response to “step” input functions, as illustrated in Figure 4.

Second-order interpolation over-shoots a step change in x by 1/8 of the actual change in x. This may produce a slight amplification of any “noise” that is present in the x_n sequence, particularly because in digital systems all changes are really step changes at the limit of resolution.

An alternative is to use point-to-point interpolation, which ensures a unique interpolation for each interval, and precludes overshoot. However, it also increases the tendency to underestimate the amplitude of actual input oscillations (recall the discussions of pre-warping in Sections 2.3.3 and 2.3.5). Also, with regard to uniqueness, it must be recognized that consistency does not imply accuracy. It is likely that in most cases both second-order interpolations for a given interval are better representations of the true function than the linear interpolation. Furthermore, since the second derivative of x appears explicitly in equation (3.1-1), we must recognize that, using point-to-point interpolation, the second derivative is zero across each interval and infinite at each breakpoint.

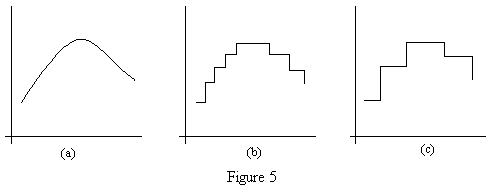
Based on the preceding remarks, it’s clear that no single interpolation scheme is best for all applications. An important consideration is the “quality” of the input signal. When the input is sampled from a smooth continuous function, as illustrated in Figure 5a, then a second-order fit will normally be more representative than point-to-point interpolation. However, when the input is sampled from a “coarse” digital representation as shown in Figure 5c, then the second derivative implied by three consecutive samples is unreliable, and point-to-point interpolation is probably preferable. In the intermediate case shown in Figure 5b the preference is less clear, but presumably the optimum representation cannot be outside the range between point-to-point interpolation and second-order interpolation. Therefore, our approach will be to derive the exact recurrence formulas for these two limiting cases.

It is shown in the next section that the ambiguity of interpolation results in only a single degree of freedom in the exact recurrence formula for a given differential equation, so the range of reasonable solutions is fully delimited by these two cases.

3.2.2  General Second-Order Recurrence Formulas

As discussed previously, the second-order recurrence formula computes yi as a function of y_i-2, y_i-1, x_i-2, x_i-1, and x_i. As the general form we propose a linear combination of these five values:

where the coefficients c₁ through c₅ are all functions of Δt and of a₁, b₁, a₂, and b₂ from equation (3.1-1). It may appear that equation (3.2.2-1) has 5 degrees of freedom, but because of the relative nature of the response, it’s clear that the five coefficients must satisfy the identity

which removes one degree of freedom. Furthermore, if we define

then equation (3.2.2-1) can be written

This shows that among all possible recurrence formulas based on reasonable interpolation schemes for a given differential equation and Δt, there is really only one degree of freedom. This is because when x_i-2, x_i-1, and x_i are co-linear versus time, the optimum interpolation is clearly linear, so we can assume that all reasonable formulas are identical for this case. Since ΔΔxi is zero in this case, the last term of (3.2.2-2) drops out, and the remaining terms must be identical for all reasonable formulas. Therefore, c₁ and c₂ are uniquely determined by this requirement, as are the sums c₃ + c₄ + c₅ and c₄ + 2c₅. Thus the general recurrence formula written in the form

has only one free coefficient, L₅, the value of which depends on the type of interpolation used when the x_n are not co-linear. The other four coefficients are fully determined by the linear case. Therefore, comparing equations (3.2.2-2) and (3.2.2-3), we see that any reasonable set of “c-coefficients” must satisfy the equations

Taking c₅ (which equals L₅) as the free variable, we can solve the last two of these equations for c₃ and c₄ to give

This shows that, within the class of reasonable coefficients sets for a given differential equation and Δt, the values of c₃, c₄, and c₅ are mutually co-linear. Hence, not only is there just a single degree of freedom among these sets, but an interpolation between any two sets varies all the coefficients in an equal proportion to their total differences.

3.2.3  Optimum Recurrence Coefficients For Second-Order Interpolation

In this section we derive the coefficients of equation (3.2.2-1) assuming that the input function x(t) is the second-degree polynomial that passes through x_i-2, x_i-1, and x_i. If we set

then a second-order curve fit of the two points gives

where

Differentiating equation (3.2.3-1) gives

Therefore, equation (3.1-1) can be written

We propose a particular solution of the form

which gives

Substituting these expressions for y and its derivatives into equation (3.2.3-2) and equating coefficients of like powers of t, we can solve for k₁, k₂, and k₃. If we define the dimensionless parameters

then we have

Now, the homogeneous form of equation (3.2.3-2) has the general solution

where

and the coefficients R₁ and R₂ are to be determined by two conditions on y(t). (Classically this is the general solution, i.e., a “basis” for all possible solutions, only if r₁ ≠ r₂. If r₁ = r₂ the expressions for R₁ and R₂ below are singular. However, these singularities are removable when the solution is expressed in discrete-time form. The solution derived from (3.2.3-4) can be shown to be identical whether or not r₁ = r₂.) Adding equations (3.2.3-3) and (3.2.3-4) (the particular and complimentary solutions respectively) gives the general total solution of equation (3.2.3-2)

We will determine the coefficients R₁ and R₂ by imposing the following two conditions on y(t): y = y_i-1  at  t = t_i-1, and y = y_i-2  at  t = t_i-2  =  –Δt.  Inserting these two conditions into equation (3.2.3-5) gives

and

Solving these two equations simultaneously for R₁ and R₂ gives

Substituting these expressions for R₁ and R₂ into equation (3.2.3-5), solving for y_i  at  t = t_i = Δt, and simplifying, we have

where g and d are dimensionless parameters defined by

Substituting the prior expressions for k₁, k₂, and k₃ into equation (3.2.3-6) and combining terms by x_n and y_n we arrive at the final recurrence formula

For a given discrete time increment Δt, the recurrence coefficients are given by

As required, the sum of c₁ through c₅ is identically equal to 1. Also, since this solution qualifies as a “reasonable” recurrence formula (in the sense that it gives x(t) as a linear function when x_i-2, x_i-1, and x_i are co-linear versus time), we can now determine the first coefficients of equation (3.2.2-3) using equations (3.2.2-4) as follows

Before proceeding to the next section we will derive three more recurrence formulas that will prove useful. They are based on equation (3.2.3-5) with the constants R₁ and R₂ determined by the two conditions  y = y_i-1  at  t = t_i-1 = 0  and  dy/dt  =    at  t = t_i-1 = 0. Inserting the first of these conditions into equation (3.2.3-5) gives

To apply the second condition we first differentiate equation (3.2.3-5) as follows

Inserting the second condition, we have

Solving equations (3.2.3-9) and (3.2.3-11) simultaneously for R₁ and R₂ gives

(3.2.3-12)

Substituting these expressions for R₁ and R₂ into equation (3.2.3-5), solving for y_i at t = t_i = Δt, and making the appropriate substitutions for k₁, k₂, and k₃, we arrive at the recurrence formula

If we define the dimensionless parameters

we can express the coefficients f₁ through f₅ in equation (3.2.3-13) as

Similarly, we can solve equation (3.2.3-10) for (dy/dt)_i  at  t = t_i-2 = Δt  with R₁ and R₂ given by equations (3.2.3-12). This leads to the recurrence formula

In terms of the dimensionless parameters

we can express the coefficients g₁ through g₅ in equation (3.2.3-14) as

Equations (3.2.3-13) and (3.2.3-14) can be used as a two-stage recurrence scheme for generating both y_n and .

Another useful recurrence formula is found by solving equation (3.2.3-5) for y_i-2 with R₁ and R₂ given by the last two of equations (3.2.3-12) and setting t = t_i-2 = –Δt. This leads to the formula

In terms of the dimensionless parameters

the coefficients h₁ through h₅ can be expressed as

3.2.4  Optimum Recurrence Coefficients Based on Point-To-Point Interpolation

In this section we derive the coefficients of equation (3.2.2-1) with the assumption that the input function x(t) is linear between successive values of x_n. As mentioned previously, this implies that the second derivative is zero during each interval and infinite at each instant t_n, where the slope changes discontinuously. Therefore, we will first determine the response to equation (3.1-1) to a discontinuous change in the derivative of x(t). Our approach will be based on the solution of the following problem:

Equations (3.2.3-13) and (3.2.3-14) provide the means of solving this problem if we can infer the appropriate values of x_i-2 and x_i from the given information. The function x(t) is uniquely determined in the interval from t_i-1 to t_i by the values of x_i-1, , , and Δt, and the requirement of a constant second derivative. Therefore, the value of x_i is also uniquely determined, and is given by

Further, if we recognize that the only purpose of x_i-2 in equations (3.2.3-13) and (3.2.3-14) is to determine the function x(t) in the interval from t_i-1 to t_i, which it does by assuming a constant second derivative over the entire double interval from t_i-2 to t_i, then it is clear that the appropriate value for x_i-2 is to be found by extrapolating the function x(t) back to t_i-2. On this basis, it can be shown that

Substituting the two preceding expressions into equations (3.2.3-13) and (3.2.3-14) gives the solution to the problem:

These equations allow us to compute the effect on y and  of a change in  from  to  occurring uniformly during an interval Δt. In the limit as Δt goes to zero these equations reduce to

With this result we can proceed to determine the general recurrence formula based on point-to-point interpolation of the input function. By equations (3.2.3-15) and (3.2.3-13) we can write

where

The synthesized values of x can be expressed as

Also, since the change in the derivative of  x(t)  at  t = t_i-1  is

we have, by equation (3.2.4-1), the relation

Making the indicated substitutions for X_i-2, X_i, and  in equations (3.2.4-2) and (3.2.4-3), and then eliminating  from the resulting equations leads to the general recurrence formula based on point-to-point interpolation

where, if we define the dimensionless parameter

the coefficients c₁ through c₅ are given by

As required, the sum of c₁ through c₅ is identically equal to 1. Also, substituting these coefficients into equations (3.2.2-4) gives the same values for L₁ through L₄ and do the coefficients based on second order interpolation (see equations (3.2.3-8)). This is in accord with the assertion that all reasonable coefficient sets give identical results when x_i-2, x_i-1, and x_i are co-linear versus time.

3.2.5  Discussion

In the preceding sections no distinction was made between the cases when the roots r₁ and r₂ of the characteristic equation are real and when they are complex. In either case the dimensionless parameters in terms of which the recurrence coefficients have been expressed are always purely real, as is easily verified using the basic exponential and trigonometric identities for complex variables. Table 2 presents a summary of these dimensionless parameters, including the equivalent trigonometric definitions where appropriate. In this table the parameter u and v are defined as

Notice that r₁ = u + iv and r₂ = u – iv.

Table 2

The use of the recurrence formulas developed in the preceding sections can best be illustrated by an example. Consider a function with a dynamic characteristic described by the differential equation

In this example we have

If we arbitrarily select an execution period of Δt = 1 sec, then by the equations in Table 2 we have

Since the function is under-damped, we use the trigonometric form of the equation for d to compute

We can now use equations (3.2.3-7) to compute the coefficients of the general recurrence formula based on second order interpolation of the input function:

We can verify that these coefficients sum to 1, as required. To demonstrate the operation of this recurrence formula we will compute the response to three different input functions:

In the first case it’s convenient to use the form of the recurrence given by equation (3.2.2-2). setting x_i-2 = 100 and  Δx_i-1 = ΔΔx_i = 0, to give the formula

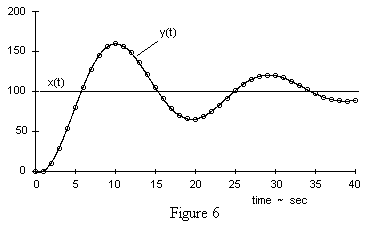
With the initial conditions y₀ = y₁ = 0, the subsequent values of y_n generated by this formula are plotted in Figure 6.

In the second case,  ΔΔx_i  is still zero, but  Δx_i-1  is a constant equal to 1 (since the slope of the function x(t) = t  is 1). Therefore, equation (3.2.2-2) gives the formula

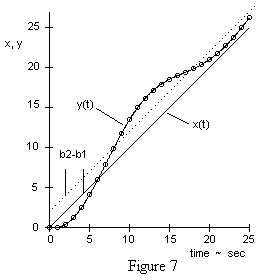
where we have substituted t_i-2 for x_i-2. With the initial conditions y₀ = y₁ = 0, the subsequent values of y_n generated by this formula are plotted in Figure 7.

In the third case, neither the first nor the second derivative of x(t) is zero, so we use the general form of the recurrence formula (3.2.2-1). Substituting for x_n the corresponding value function of t_n, we have

With the initial conditions y₀ = y₁ = 0, the subsequent values of y_n generated by this formula are plotted in Figure 8.

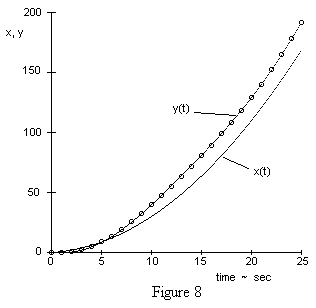
Figure 9 shows the response to the same input function from the initial conditions y₀ = y₁ = 50.

In these examples the computed values of y_n fall exactly on the theoretical function y(t), because all the input functions are exactly representable by a second-degree polynomial. Any choice of execution period will yield the same accuracy. For example, if we had chosen Δt = 5 sec, the coefficients would have been different but the computed values of y_n would still have fallen exactly on the theoretical function y(t). The only consideration limiting the size of Δt in such cases is that the output of y_n must occur frequently enough to adequately represent the function y(t) for external purposes.

In practice, the continuous input function x(t) is usually specified by a sequence of discrete values from some external source, rather than computed from a given equation as in the preceding examples. It is the lack of a precise functional definition of x(t) that requires us to assume an interpolation function for the xn sequence. This, in turn, requires that Δt be small enough so that our interpolation of the x_n samples is sufficiently representative of the true continuous input function f(t). This restriction on Δt should not be confused with a restriction arising from the use of a non-optimum solution method, as discussed in Sections 2.3.5 and 3.3.5.)

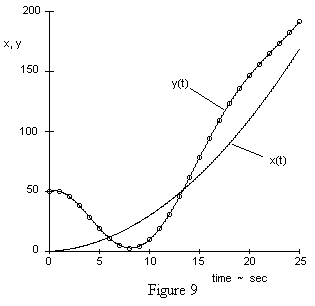
We can also determine the optimum recurrence formulas for the dynamical system specified by equation (3.2.5-1) with the assumption of point-to-point interpolation of the input samples. Since the point-to-point formula is identical to the second-order-fit formula when x_i-2, x_i-1, and x_i are co-linear versus time, they give identical results for the constant and ramp inputs i.e., cases (1) and (2) above. It is only when applied to the third, more general, case that the two assumptions give different results. To determine the exact point-to-point recurrence formula, we first compute the dimensionless parameters

using the equations in Table 2. Then by equations (3.2.4-4) we can compute the coefficients of the exact point-to-point recurrence formula

These coefficients differ hardly at all from those computed on the basis of second-order interpolation, so the predicted response to the input for case (3) is virtually identical to that given by the second-order-fit method, especially since every three consecutive samples x_n are nearly co-linear.

To conclude this section, we will develop the “standard form” of the second-order recurrence formula (analogous to equation (2.2.2-2) for first-order formulas), in terms of which the optimum second-order solutions can be expressed succinctly. If we define

then equation (3.2.2-2) can be written as

Since the coefficients sum to unity we have c₃ + c₄ + c₅ = 1 – c₁ – c₂, so we can make this substitution to give

which can be written as

Thus we have the “standard form” for second-order recurrences

where

and the D coefficient is given by

for second-order interpolation, and by

for point-to-point interpolation. It’s worth recalling that the set of all reasonable second order recurrence schemes has just a single degree of freedom, which can be linearly parameterized by the D coefficient of the standard form.

Return to Table of Contents