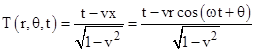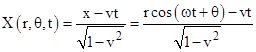|
|
|
If a circular disk of radius R is rotating with an angular speed ω in equilibrium about its center, while the center is translating uniformly in the plane of rotation with velocity v (in terms of a fixed system of inertial coordinates), then the portions of the rim at right angles to the direction of translation are moving with speed v increased or decreased by approximately ωR. With respect to the rest frame inertial coordinates of the disk's center, the disk is perfectly circular (by definition), but, with respect to the "stationary" coordinates in terms of which the disk's center is moving at the speed v, the spatial extent of the disk in an "instant" is shortened into an ellipse, with the shorter axis pointing in the direction of travel. This may seem to imply that the transformation is symmetrical about the axis of translation, contradicting the fact that the opposite edges of the disk are moving at different speeds with respect to the "stationary" coordinates. However, the result of the Lorentz transformation applied to a spinning disk is not actually symmetrical about the axis of translation. |
|
|
|
In terms of the inertial coordinates of the disk's center, a point on the disk at the location r,θ (fixed with respect to the disk) and the time t is |
|
|
|
|
|
If we now consider a system of coordinates T,X,Y with respect to which the disk's center is moving uniformly in the negative x direction with speed v, then the Lorentz transformation gives |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Our objective to determine the configuration of the points of the disk with respect to these coordinates at a given "instant". From the equation for T(r,θ,t) we see that at the instant T = 0 we must have |
|
|
|
|
|
|
|
The values of v and ω are fixed, so for any gives values of r and θ we can solve this "Kepler equation" for t(r,θ). By definition this value of t gives T = 0. We can then insert this value of t into the equations for X(r,θ,t) and Y(r,θ,t) to give the coordinates of the point [r,θ] on the disk. We can also substitute vrcos(ωt + θ) for t in the expression for X. This gives the result |
|
|
|
|
|
|
|
|
|
|
|
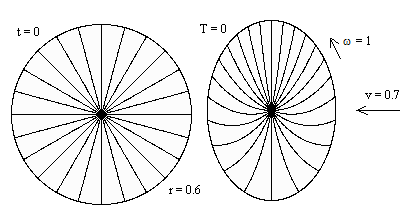
Obviously the spatial outline of the disk is an ellipse with respect to these coordinates, and this shape is symmetrical about the axis of translation. However, the spatial mapping of the points of the disk is not symmetrical, because the rotation of the disk causes the lower part to have a lower velocity (with respect to the "stationary" coordinates) than the upper part. If we plot lines on the disk that represent in the x,y,t coordinates purely radial loci of constant θ, we find that these loci map to more complicated curved with respect to the X,Y,T coordinates, as illustrated below. |
|
|
|
|
|
|