The Prismoidal Formula
One of the oldest documents in existence is a papyrus roll written in Egypt around 1890 BC. This is sometimes called the Golenischev Papyrus, after the Russian who purchased it in Egypt in 1893 and brought it to Moscow, where it remains today. It is also commonly called the Moscow Papyrus. It's about 18 feet (544 centimeters) long, and about 4 centimeters wide, and the writings consist of 25 mathematical problems with solutions. By far the most intriguing of these is the 14th, which asks for the volume of a truncated pyramid (frustum). Roughly translated, it says
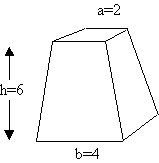
Given a truncated pyramid of height 6, base 4, and top 2, you are to square the bottom, multiply the bottom by the top, square the top, and add all these to give 28. Then you are to multiply this by a third of the height to give the right answer, 56.
The type of solid described in this problem is illustrated below, with a, b, and h signifying the linear measures of the top, bottom, and height respectively.
In modern notation the Egyptian method of finding the volume can be expressed by the formula
![]()
The level of sophistication of this result is quite a bit higher than that of the rest of the papyrus (for example, the same papyrus gives incorrect formulas for some relatively simple plane areas), leading some people to suspect that either the Egyptians just stumbled into this particular formula, or else perhaps it was part of a more advanced body of mathematical results not generally reflected in the papyrus. Incidentally, according to tradition the god Thoth (Djhowtry), originally associated with time and the Moon, gave the calendar, astronomy, and mathematics ("reckoning") to the Egyptians. Thoth was later identified with the Greek god Hermes, who was later called Hermes Trismegistos (thrice great), the supposed author of the hermetic works revealing the secret knowledge of the ancients. Even as late as the 1600's this tradition was still influential in Europe. Isaac Newton, for example, was a devotee of hermetic studies, and actually seems to have believed that his own discoveries, such as calculus, universal gravitation, and much more, had been in the body of secret knowledge handed down from Thoth! Not surprisingly, Newton usually kept ideas like that to himself.
In any case, notice that the above formula can be re-written in the form
![]()
The quantity inside the inner parentheses is 4 times the square of m = (a+b)/2. Obviously m is the linear dimension of the horizontal slice through the solid mid-way between the top and the bottom surfaces, and m2 is the area of this mid-slice. Hence the Egyptian formula can be interpreted as giving the volume of any frustum in terms of the areas A1, A2, A3 of the top, middle, and bottom slices
![]()
This is interesting because it is identical to what is known in calculus as Simpson's Rule of integration. In general if f(x) is any polynomial of degree less than or equal to 3, then we have
![]()
![]()
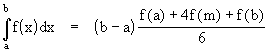
![]()
![]() (1)
(1)
where m = (a+b)/2. It's easy to see why this is true for quadratic f(x), because it's essentially just the familiar integration rule for powers. For example, if we have f(x) = x2, then the indefinite integral of f(x) is (1/3)x3, which implies that the definite integral from a to b is
![]()
This is identical to the rule described in the Moscow papyrus, bearing in mind that the area of a horizontal slice through a pyramid is proportional to the square of the distance from the (projected) apex of the pyramid, so we have A(x) = x2. (Notice that this applied to truncated pyramids whose bases have any shape, not just square as drawn above. Hence the expression is sometimes called the prismoidal formula.)
It is perhaps slightly less obvious that this same integration rule (1) applies to the general cubic polynomial f(x) as well. If we set f(x) = x3, the indefinite integral is (1/4)x4, so the definite integral from a to b is
![]()
This can be re-written in the form
![]()
The quantity in the inner parentheses on the right side is 8 times the cube of m = (b+a)/2, so this again reduces to equation (1).
Similarly we can show that equation (1) applies to the general cubic polynomial. If we have f(x) = Ax3 + Bx2 + Cx + D then the definite integral is given by
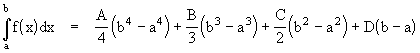
Factoring out the width (b - a) from each term and placing all the terms over a common denominator, the right hand side can be written as
![]()
Re-arranging terms, we have
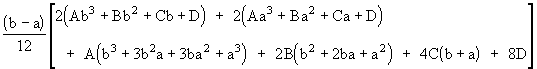
Noting that the quantities in parentheses in the lower row on the right are 8m3, 4m2, and 2m respectively, where m = (b+a)/2, we arrive again at equation (1).
Not surprisingly, equation (1) is not exact for polynomials of degree greater than 3, but it is possible to devise analogous formulas applicable to higher degree polynomials in terms of the value of the polynomial at a sufficient number of intermediate values of x. In general a unique polynomial of degree d passes through d+1 given points, so if we specify the values of f(x0), f(x1), f(x2), ..., f(xd) we can determine the coefficients of f(x), from which we can determine the definite integral of f(x) from x0 to xd.
To illustrate, suppose f(x) is a polynomial of degree 2 and we are given the values of f(x0), f(x1), and f(x2) where x1 = x0 + l (x2 - x0) for some constant l . We can then easily determine the definite integral
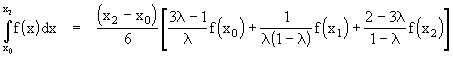
If we take l =1/2, so that x1 is mid-way between x0 and x2, we again get the ancient Egyptian formula
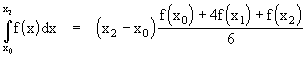
This is often called Simpson's Rule, named after Thomas Simpson (1710-1761), who published it as a means of approximating the integrals of functions, assuming they are nearly equal to the quadratic arc through three consecutive equally spaced points. (The same formula had actually been published by James Gregory in 1668, but of course neither Simpson nor Gregory has priority over the Moscow papyrus circa 1890 BC!) Simpson was an interesting man, with a decidedly non-intellectual family background. His father was a weaver, and Thomas was expected to take up the same occupation, but after witnessing a solar eclipse at the age of 14 he somehow became interested in mathematics. According to Rouse Ball's history, Simpson then learned the basics of arithmetic and algebra "with the aid of a fortune-telling peddler". After this, Simpson managed to get himself into a school (entirely by his own efforts) so as to continue his mathematical studies. Finally at the age of 33 he was appointed as professor of mathematics at Woolwich college in London. He seems to have been a man of extraordinary natural genius, and wrote treatise on many difficult subjects, including a study of the irregularities of the lunar orbit that had defeated even Newton. In 1747 he successfully solved for the motion of the apse of the lunar orbit. Unfortunately for Simpson, Clairaut had solved the same problem (by a different method) just two years earlier.
The fact that this "Simpson's Rule" is exact for cubic as well as quadratic curves has the interesting consequence that the areas between the unique quadratic and any cubic polynomial through the same three equally-spaced points must be equal on either side of the center point. This is illustrated in the figure below.
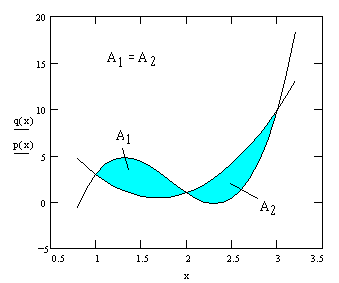
By the same method we can find expressions for the definite integral of polynomials of higher degree in terms of their values at a sufficient number of equally-spaced points. This can be conveniently done by means of Lagrange's n-point interpolation formulae. The results, called Newton-Cotes formulas, are summarized below for the first several polynomial degrees. We will normalize these by dividing through by the interval xn-x0 so that the right hand side represents the mean value of the function f(x) on the interval.
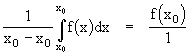
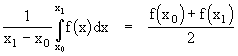
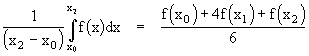
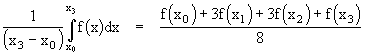
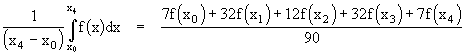
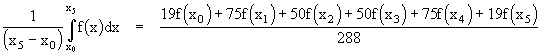
The first two are exact for polynomials up to degree 1, the next two are exact for polynomials up to degree 3, and next two are exact for polynomials up to degree 5, and so on. Obviously the sum of the coefficients in the numerator equals the denominator, so each of the "mean" formulas is just a weighted average of the evenly-spaced values of the function. Carrying this further, we can construct the following table of coefficients.
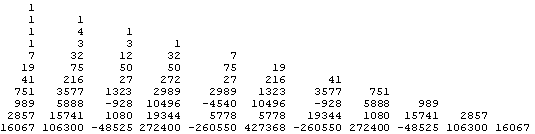
The expressions with these coefficients are sometimes called Cotesian formulas, named after Roger Cotes (1682-1716), who a best known as the editor of the second edition of Newton's Principia. It was Cotes, in his lengthy introduction to the 2nd edition, who actually was the first to articulate much of what came to be regarded as the Newtonian world view. When Cotes died at the age of 34, Newton said "if he had lived, we might have known something". (It's interesting that, at least in the case of Simpson's Rule - which is the simplest of the non-trivial Newton-Cotes formulas - Newton was arguably justified in his seemingly outlandish view that he and others were just re-discovering the knowledge of the ancient Egyptians.)
Notice that, beginning with the 8th-degree case, some of the Cotesian coefficients are negative, meaning that the "weights" of those points in the average are negative. We might consider carrying on this analysis to the nth-degree case in the limit as n goes to infinity, but the values of the "weights" do not converge at any fixed point in the interval.