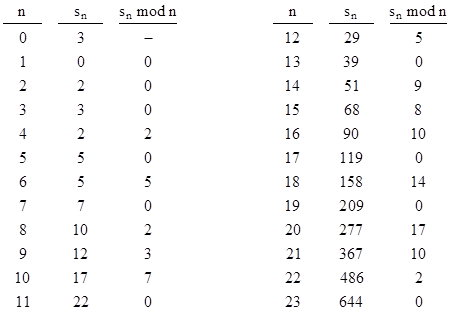Spiral Tilings and Integer Sequences

It’s well known that the plane can be tiled by a spiral of geometrically increasing squares as shown below.

This overall shape is sometimes called the “golden rectangle”. Letting S_n denote the length of the side of the nth square in this spiral, we see by inspection that the edge lengths satisfy the Fibonacci recurrence S_n = S_n−1 + S_n−2. Also, letting ϕ denote the ratio S_n/S_n−1, it follows that ϕ is a root of the characteristic equation

The two roots of this polynomial are the well-known “golden proportion”, also known as the extreme and mean ratio of the ancient Greeks:

Letting f_n denote the sum of the nth powers of these two roots, the values of f₀, f₁, f₂, … etc., are 2, 1, 3, 4, 7, 11, etc.  These values (sometimes called the Lucas sequence) satisfy the same recurrence relation as do the edge lengths of the squares in the spiral tiling pattern. Notice that if p is a prime, then f_p is congruent to 1 modulo p. (In other words, f_p is exactly 1 greater than a multiple of p.) In contrast, composite integers n for which s_n = 1 (mod n) are quite rare, the smallest being 705. This is why the Lucas sequence can be used as probabilistic primality test.

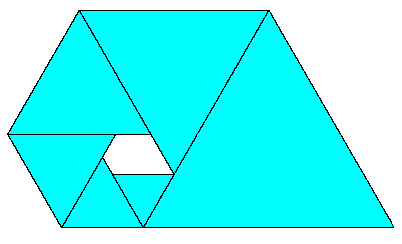
Somewhat less well known is the plane tiling consisting of a spiral of geometrically increasing equilateral triangles as shown below.

Considering the popularity of the "golden rectangle", it's surprising that this analogous construction for equilateral triangles is so rarely mentioned, especially since this pattern has probably been re-discovered by almost everyone who has ever considered spiral tilings. It could easily have been found by the ancient Greeks, but there is no evidence that they ever studied this kind of pattern. Notice that if h_k denotes the height of the kth triangle in the spiral, then each of the following recurrences is satisfied

This corresponds to the fact that the sequence has the two characteristic equations

This isn't surprising, because the second polynomial is a divisor of the first, i.e.,

Each triangle in the sequence is larger than the preceding triangle by a factor α defined as the real root of the cubic factor x³ − x − 1. This value can be expressed as

The numerical value of this expression is

The other two roots of this cubic polynomial x³ − x − 1 are

Letting s_n = αⁿ + βⁿ + γⁿ denote the sum of the nth powers of the three roots, it follows that s₀ = 3, s₁ = 0, s₂ = 2, and s_n = s_n−2 + s_n−3 for all n greater than 2. The table below lists the first several values of s_n, along with the remainders of s_n when divided by n, i.e., the values of s_n modulo n.

Notice that for any prime integer p the number s_p is divisible by p, and hence we have s_p = 0 (mod p). In contrast, if n is composite, then s_n is almost never divisible by n.  The smallest composite n that divides s_n is 271441 = (521)².  This was first found by Shanks and Adams in 1982, and doubtless re-discovered many times since then. This shows that the primality test based on Perrin’s sequence is much stronger than the one based on the Lucas sequence. The only other “Perrin pseudoprime” of this kind less than 1 million is 904631 = (7)(13)(9941). The next composite n that divides s_n is 16532714 = (2)(11)(11)(53)(1289), which is also the first even pseudoprime of this kind.  Just for good measure, the next composite n that divides s_n is 24658561 = (19)(271)(4789).

The recurrence for s_n can also be applied in the negative direction, and it gives integer values for negative indices. The requirement s_n = 0 (mod n) is really only half of the full pseudoprime test based on x³ – x − 1.  The other half is s_−n = −1 (mod n).  Every prime satisfies both of these congruences, but the smallest composite that satisfies both of the congruences is 27664033 = (3037)(9109), which was also first discovered by Shanks and Adams. All of this is really just a special case of a much more general subject, in which we can determine congruence conditions on the terms of arbitrary linear recurring sequences with arbitrary initial values. This is discussed in the note on symmetric pseudoprimes.

By the way, it's not hard to show that the elements of the s_k sequence have the closed form expression

where r = 0, 1, 2, 3, 4, or 5, and a,b are the least non-negative integers such that a = r (mod 2) and b = −r (mod 3).

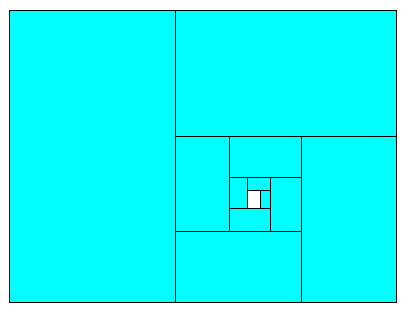
It’s also possible to construct a geometrical spiral tiling of similar rectangles based on the Perrin recurrence, as shown in the figure below.

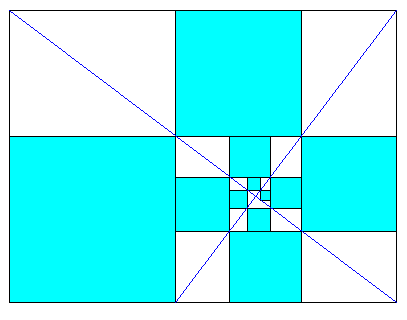
Letting L_n and W_n denote the length and width of the nth rectangle, we see by inspection that L_n = W_n−1 + L_n−2. Therefore, if k denotes the constant ratio L_n/W_n, and if α denotes the constant ratio L_n/L_n−1, we have kα² = α + k and hence k = α/(α² – 1). If we then stipulate that k = α², it follows that α³ = α + 1, so α is the real root of Perrin’s cubic given previously. It also follows that L_n – W_n−1 = W_n, which implies that if we extend the length-wise edge line through the subsequent width, we have a spiral sequence of perfect squares, as shown below.

These squares are inscribed at a characteristic angle between two perpendicular lines. The successive squares in the spiral increase in size by the factor α. For more on this ratio and the related numerical sequence, see the note on Perrin's Sequence.

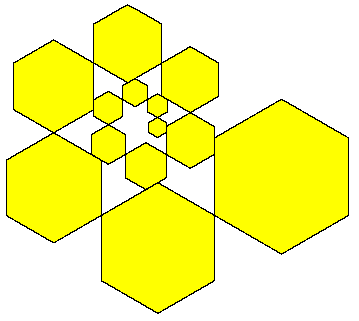
In a similar way we can construct tilings based on other regular polygons. For example, consider the geometrical spiral of hexagons shown below.

Letting ρ denote the ratio of the edge lengths of successive hexagons, and letting R denote the width of the smallest hexagon shown in this figure, we can determine the characteristic equation by noting how the horizontal locations of the right hand edges of the hexagons vary, beginning with the smallest. The right hand edges of the first and the sixth hexagons are aligned, so we have

Canceling R and simplifying, we find the characteristic equation is

The only real root of this quintic is ρ = 1.185749553766…, so this is the ratio of the edge lengths of successive hexagons in the spiral depicted above. This polynomial is not monic (i.e., the leading coefficient is not 1), but the polynomial with the reciprocal roots is

and this is monic, so we can conveniently use the corresponding recurrence to construct a sequence of integers analogous to the Lucas and Perrin sequences. Letting H_n denote the sum of the nth powers of the roots of this quintic, we have the initial values

and the subsequent values in the sequence can be computed using the recurrence

As always, if p is a prime, then H_p is congruent to H₁ modulo p. This particular sequence happens to contain numerous “pseudoprimes”, such as 25, 215, 265, etc, but these can be discounted if we eliminate all multiples of 5. For the remaining numbers, we find three relatively small pseudoprimes 1843 = (19)(97), 9362 = (2)(31)(151), and 9889 = (11)(29)(31). After these, the next pseudoprime for this sequence is 399122 = (2)(197)(1013).

Return to MathPages Main Menu