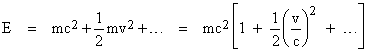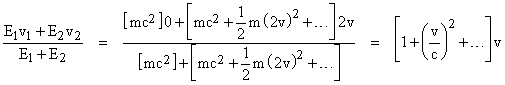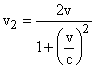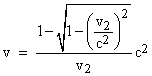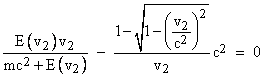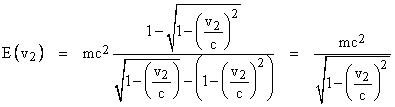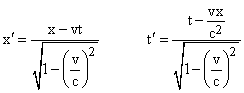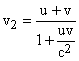The Center of Energy

Special relativity is sometimes presented as if it was a surprising departure from previous ideas, but it was actually fairly inevitable as soon as the concept of energy as a conserved quantity was accepted. Today the energy principle is so central to physics, and is taken so much for granted, that we sometimes forget how recently it was formulated. Only in the mid-19th century, beginning with the work of Mayer and Joule, was the conservation of energy recognized. Of course, prior to that time there had been discussions of various kinds of energy, but those individual kinds of energy could pass in and out of existence, so energy was not generally seen as a conserved quantity.

One of the first individual forms of energy to be explicitly discussed was kinetic energy. Soon after Newton formulated his laws of mechanics, a dispute arose with Leibniz over what should be regarded as the most meaningful measure of motion. The Newtonians gave primacy to what we call momentum, i.e., the product of mass and velocity, which Leibniz called vis mortua (the dead force), distinguishing it from what he called vis viva (the living force), which was the product of mass and the square of the velocity. This latter quantity is proportional to what we now call the kinetic energy. Notice that the velocity v is a vector, so the momentum mv is also a vector, whereas the kinetic energy (1/2)m|v|² is a scalar quantity.

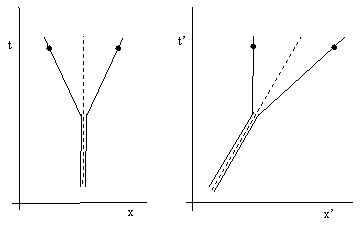
From the modern perspective, Newtonian mechanics contains a rather glaring anomaly, because while the center of mass of an isolated system of particles moves uniformly in a straight line, the center of energy does not. Consider an isolated system consisting of two identical particles, each of mass m, initially stationary at the origin of an inertial coordinate system x,t. At some instant the particles exert a mutual impulse (by the release of some stored energy, perhaps of a massless spring that had been compressed between them), causing them to move away from the origin at the speeds +v and –v. The center of mass remains stationary at the origin, as does the center of energy. This is illustrated in the left-hand figure below.

The central dashed line in the left-hand figure represents the path of both the center of mass and the center of energy (potential and kinetic). The figure on the right represents the same situation in terms of a system of inertial coordinates x’,t’ moving with speed –v relative to the original system of coordinates. In terms of these coordinates the two particles are originally moving to the right with speed v, and, after repelling each other, one particle is left stationary and the other is moving to the right with speed 2v. In this case the (sloping) dashed line still represents the centers of mass and energy prior to the repulsion event, and after the repulsion event the continuation of the dashed line still represents the center of mass, but it obviously does not represent the center of energy. The original potential energy moving along with the particles is converted to kinetic energy of the particle when they separate, but the stationary particle has no kinetic energy at all relative to this frame, and the particle moving with speed v has kinetic energy (1/2)m(2v)², so the center of energy follows the latter particle. Thus the path of the center of energy of an isolated system, not subjected to any external influence, changes course abruptly.

Of course, we are treating kinetic energy as a relative quantity, but momentum is also treated as a relative quantity. The principle of relativity, founded by Galileo, was a fundamental feature of Newtonian mechanics (not to mention our intuitive conceptions). When we combine the Galilean principle of relativity with the 19-century belief that energy has a permanent existence, that can neither be created nor destroyed but merely moved from place to place, then energy (kinetic and potential) in Newtonian mechanics becomes anomalous.

Moreover, there seems to be only one conceivable way of solving this problem. In order for the center of energy to coincide always with the center of mass for an isolated system, for any possible internal interactions within the system, we must require that “mass” and “energy” for each localizable entity are strictly proportional to each other. In other words, we must have, quite generally, the relation E = mk for some universal constant k, where m signifies the usual mass of a particle having zero kinetic energy. We will call m the “rest mass” of the particle. Notice that the constant k has units of squared velocity, so we can write k as c² where c denotes some universal speed (whose identity or significance isn’t immediately clear). These considerations imply that there is only a single degree of freedom for the mass-energy of any localizable entity, and hence we must regard mass-energy as a single attribute. Consequently, letting E now denote the total mass-energy in units of energy, it follows that the mass-energy of a stationary particle can be written as E = mc². We also know that if this particle is viewed from a system of inertial coordinates in terms of which it has velocity v, then it has some additional amount of mass-energy, which in units of energy is roughly equal to the Newtonian quantity (1/2)mv², at least for small velocities v. Thus we expect the total mass-energy E of a particle of mass m moving with speed v to be given at least approximately by

This, in turn, has another very important implication, which we can see by considering again the system of two isolated particles in terms of the x’,t’ coordinate system. Let v₁ and v₂ denote the velocities of the two particles after the repulsion event. The velocity of the center of mass-energy prior to the repulsion event is v, and we have v₁ = 0. If the velocity of the rightward-going particle after the repulsion event were v₂ = 2v (as it would be in Newtonian mechanics) then the velocity of the center of mass-energy would be

The leading factor in the right-hand expression shows that the center of energy of this isolated system still changes its trajectory, albeit only by a factor that differs from one by a quantity of the second order in v/c. If we believe the trajectory of the center of mass-energy of an isolated system does not change, we are compelled to accept that the velocity of the rightward particle is not quite 2v, but is actually (at least up to second order) equal to

Admittedly for values of v that are very small compared with the constant c this is a very small effect, but it has profound implications. We know the rightward particle has velocity v relative to the inertial coordinates x,t of the original center of mass, which has a velocity v relative to the x’,t’ coordinates, and yet the velocity of the rightward particle in terms of the original coordinates is not 2v, as we would expect by applying a Galilean transformation. Hence inertial coordinate systems are not related by Galilean transformations – although the deviation is extremely small for velocities much less than c.

Our equation for v₂ is good only up to the second order in v/c. The denominator could conceivably include additional terms in higher even orders, but to determine those we would need to know the higher-order terms in the expression for E. However, the above expression for v₂ already possesses some nice properties, that would be ruined if more terms were added. In particular, notice that if v were greater than c, the value of v₂ would be less than v, which is physically implausible, since it implies that the “rightward” particle is moving to the left of the original trajectory. This implies that c must be an upper limit on speeds, and from this we expect that v₂ should approach c as v approaches c, which is indeed the case for our second-order expression. We’ll return to this question below, but for the moment we tentatively conclude that v₂ is given exactly by the above expression, with no additional terms.

But now we still have a (very slight) anomaly, assuming we accept that the mass-energy of a particle of mass m and speed u is exactly E(u) = mc² + (1/2)mu², because our formula for the speed of the center of energy following the repulsion now gives

Thus it differs from v by a factor that differs from 1 by a quantity of the 4th order in v/c. To make the velocity of the center of energy exactly unchanged by the internal repulsion event, we must solve the following equation for the function E.

Our expression for v₂ as a function of v can be solved for v as a function of v₂, giving

Making this substitution into the preceding equation, we need the mass-energy function to satisfy the relation

This gives the result

If we square both sides and clear the denominator, this relation can be written in the form

The quantity inside the parentheses on the left side can be written as

This shows that this quantity is asymptotic to c times the Newtonian momentum (vis mortua) for small velocities, so we are led to identify this with the exact momentum in the new dynamics, corresponding to the expression for mass-energy. Note that this is proportional to the first power of the particle’s velocity, so in general three-dimensional space it is a vector. Letting p denote this momentum, we can write the prior equation as

If we choose units such that c = 1, this relation has the even simpler form m² = E² – p².

We previously gave just a plausibility argument for taking v₂ exactly equal to 2v/[1+(v/c)²] with no higher-order corrections, but there is actually no ambiguity in the choice of this function. As soon as we have concluded that the relationship between relatively moving systems of inertial coordinates (defined by the relativity principle) are not related by Galilean transformations, it can be shown that the only self-consistent alternative is the Lorentz transformation

for some finite constant c. From this it immediately follows that if the primed coordinate system has speed u relative to the unprimed coordinates, and if a particle has the speed v relative to the primed coordinates, then the speed v₂ of the particle in terms of the unprimed coordinates is given by the composition formula

which of course reduces to our previous expression for v₂ when u = v.

In summary, we can see that special relativity emerges unavoidably from elementary considerations of dynamics, as soon as we attempt to reconcile the relativity of Newtonian mechanics with the principle of energy conservation.

Return to MathPages Main Menu