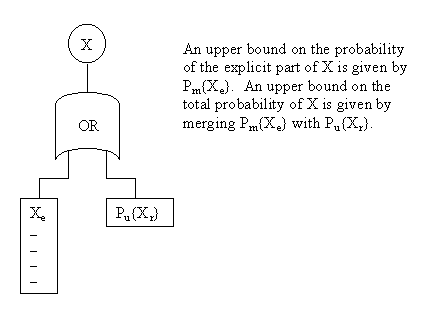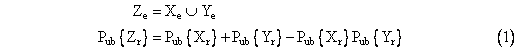Evaluating Probabilities of Boolean Events

An analysis of the failure modes and probabilities of complex systems may involve hundreds of independent variables. In general the maximum number of mincuts of a Boolean function in n variables is O(2ⁿ), so an explicit evaluation of each individual mincut is computationally prohibitive. In fact, it's known that the logical evaluation of a Boolean function of n variables is NP-complete. A typical approach to estimating the probability of a given monotone Boolean function of n variables (whose individual probabilities are known) is to truncate the evaluation by considering only mincuts with fewer than a certain number of variables, or mincuts with probabilities less than a certain cutoff value. However, neither of these strategies guarantees that all the collectively significant failure modes will be covered. Thus, such computations do not actually provide any well-defined bounds on the probability of system failure.

An interesting technique for determining rigorous bounds on the probability of a large monotone Boolean function is to partition each sub-event into an "explicit part" and a "residual part" while the function is being expanded. The explicit part of each event consists of a list of all the individual mincuts with probability greater than some threshold P_t. The residual part is a single numerical value that represents an upper bound on the probability of the union of all the mincuts for that event with individual probabilities less than P_t. Each event is represented by the logical union of these two parts.

For any event X let X_e and X_r denote the explicit and residual parts, respectively. For each of the n input variables the explicit part is just the mincut consisting of the variable itself, and the residual part is the empty set with a probability upperbound of 0. (It's possible for the probability of an input variable to be less than P_t, but normally P_t is set small enough so that every input is explicit.) All that's needed are rules for expanding the expression by carrying out the logical AND and OR operations while preserving the partitioned structure of the resulting events.

For any two events  X = X_e U X_r  and  Y = Y_e U Y_r  we can form the union Z = X U Y in terms of the partition components as follows

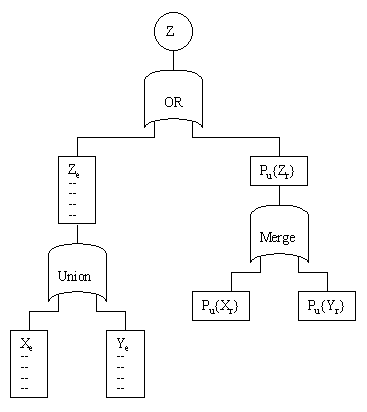
where P_ub{} signifies an upper bound on the probability. Notice that the expression for P_ub{Z_r} is the same as the expression for the probability of the union of two independent events, whereas in general we don't know if X_r and Y_r are independent or not. However, it can be shown that this expression gives an upper bound for arbitrary non-exclusive events, i.e., events formed by a monotone function. It's also easy to see that the partition is preserved, i.e., Z_r consists of all the mincuts of Z with individual probabilities greater than P_t, and P_ub{Z_r} is an upper bound on the union of all the mincuts of Z with individual probabilities less than P_t. This union operation is illustrated schematically below:

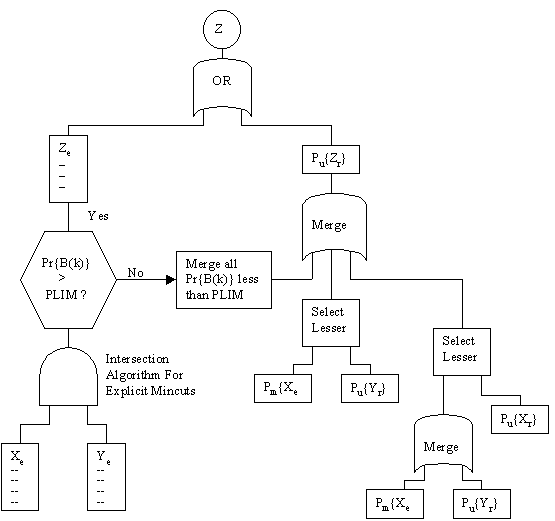
For convenience, the operation of computing an upper bound on the probability of the union of two or more events A,B,C... according to equation (1) will be denoted by Merge[A,B,C,...]. Now, for any two events X = X_e U X_r and Y = Y_e U Y_r we can form the intersection Z = X ∩ Y in terms of the partition components as follows:

 (1)  Generate the mincuts given by X_e ∩ Y_e.  Those with probability greater than P_t constitute Z_e. The others are placed in a temporary set Z_ee.

 (2)  Compute P_ub{Z_r} as follows

This operation preserves the partition, meaning that Z_e consists of all the mincuts of Z with individual probabilities greater than P_t, and P_ub{Z_r} is an upper bound on the probability of the union of all the mincuts with individual probabilities less than P_t. (Note that Step 2 is asymmetric with respect to X and Y. Transposing those two events also gives a valid upper bound; in practice we would use whichever one gives the lower value.) This intersection algorithm is illustrated schematically below:

The above procedures enable us to expand any monotone Boolean function and produce a rigorous upper bound on the overall probability, even though we have explicitly generated only a small fraction of all the mincuts. To determine a lower bound we can simply evaluate the first two sums of the inclusion-exclusion formula for the explicit mincuts of the top level event. Of course, the bounds determined in this way are not guaranteed to converge unless P_t is set to zero. However, in practice this approach is generally quite robust, in the sense that the upper bound approaches the lower bound for quite reasonable values of P_t. 

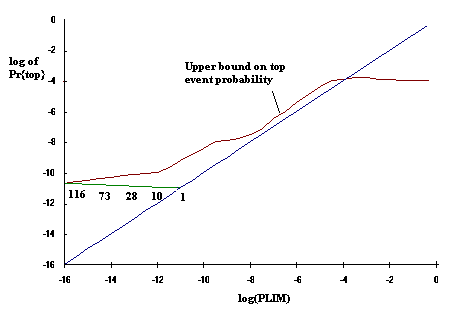
The profile of P_ub{F} vs P_t for a large Boolean function F is quite interesting. With P_t = 1 the entire expansion is carried out in residual form, with no explicit mincuts at all. This normally gives a very conservative upper bound, which I call P₀. The upper bound stays roughly constant at P₀ until P_t is reduced to about one order of magnitude smaller than P₀, at which point the profile starts to drop towards the lower bound at a rate roughly parallel to the line P_ub{F} = P_t. A typical profile is shown below, along with an indication of the number of explicit mincuts occurring at the top level

It would be interesting to know how much of a function's structure could be inferred from knowledge of it's P_t profile.

Return to MathPages Main Menu