Newton's Birth Date and The Anni Mirabiles

It's usually said that Isaac Newton was born on Christmas Day, but there is some ambiguity in this because England was still using the "old" Julian calendar at the time of Newton's birth, whereas the rest of Europe had adopted the "modern" Gregorian calendar (later adopted by England and still in use today). According to the modern calendar, Newton was born on 4 January 1643, but according to the calendar in force at the time and place of his birth, he was born on 25 December 1642. (It's been speculated that this fact held some significance for the mystical side of Newton's imagination, and helps to explain his fascination for biblical interpretation, since he can hardly have failed to notice that he was born on Christmas Day with no worldly father - his natural father Robert, a farmer, having died some 3 months before Isaac's birth.)

An even trickier question is whether Newton was born in the same year Galileo died (as is commonly said). Galileo died on 8 January 1642 (Gregorian) and Newton was born on 25 December 1642 (Julian). But when placed on the same calendar the two events fall in different years. To make things even more confusing, many English of that time still considered March 25 to be the first day of the calendar year, so by the old English reading of the Italian calendar, Galileo died in 1641. (Incidentally, since Einstein was known to have revered Maxwell, could it have escaped his notice that he was born in the same year Maxwell died?)

Originally the Romans considered the year to begin on March 1, which is the reason February (the "last" month of the year) is truncated at 28 days, and is used to sneak in an extra day every four years. This also explains why the prefixes of our month names are all "off" by two, i.e., september, october, november, december. The Romans officially recognized January 1 as the first day of the year in 153 BC, but it didn't catch on everywhere right away.

By the way, it's interesting to note that the "Julian period" (not to be confused with the Julian Calendar) well known to historians and astronomers, was named not after Julius Caesar, but after the father of Joseph Scaliger, who in 1582 devised the scheme by which each day is consecutively numbered beginning with January 1, 4713 BC, which Joseph thought would cover everything of interest.

Another ambiguous date associated with Newton is his famous "annus mirabilis", or year of miracles, around 1666. This was the period during which Isaac, having been sent home from college because of the Plague epidemic, occupied his time by inventing calculus, discovering the chromatic composition of light, and conceiving of the inverse-square law of universal gravitation... or at least this is how Newton later represented things. Of course, it must be remembered that in later life Newton was embroiled with priority disputes, most notably with Robert Hooke over optics and the inverse-square law of gravity, and with Leibniz over the Calculus. Thus, it was always in Newton's self-interest to place his discoveries as early as possible. The documentary evidence suggests that, at least with regard to mechanics and gravitation, his ideas hadn't actually reached a coherent state until much later, around 1685-1687, when he was actually composing the Principia.

Nevertheless, it's clear that Newton devoted himself intensively to the study of mathematics and physics during the intermission from Cambridge, but it's often been pointed out that his burst of activity should really be called "anni mirabiles", since it covered the time from 1664 to 1667, and much of that time he was actually at Cambridge. The school closed in the summer of '65, and Newton returned in March of '66 when the school was re-opened after the plague had gone dormant over the winter. The plague re-appeared so Cambridge was closed again in June of '66. This time it remained closed until April of '67, when Newton again returned to Trinity college.

Notwithstanding the caveat mentioned above about Newton's vested interest in recalling early dates for his discoveries, it's still interesting to read his famous recollection of his activities during these years. Following his death, part of a draft letter apparently written to the Huguenot scholar Pierre Des Maizeaux was found among Newton’s papers, and it contains this description:

In the beginning of the year 1665 I found the Method of approximating series & the Rule for reducing any dignity of any Binomial into such a series. The same year in May I found the method of Tangents of Gregory & Slusius, & in November had the direct method of fluxions & the next year in January had the Theory of Colors & in May following I had entrance into the inverse method of fluxions. And the same year I began to think of gravity extending to the orb of the Moon & (having found out how to estimate the force with which a globe revolving within a sphere presses the surface of the sphere) from Keplers rule of the periodical times of the Planets being in sesquialterate proportion of their distances from the centers of their Orbs, I deduced that the forces which keep the Planets in their Orbs must be reciprocally as the squares of their distances from the centers about which they revolve: and thereby compared the force requisite to keep the Moon in her Orb with the force of gravity at the surface of the earth, and found them answer pretty nearly. All this was in the two plague years of 1665 and 1666. For in those days I was in the prime of my age of invention & minded Mathematics & Philosophy more than at any time since.

Although he says his results "answer pretty nearly", it seems that at the time he was dissatisfied with the disagreement between his rough calculation and his observations. His surviving notes from the late 1660's show that he was using an estimate of 60 miles per degree of latitude. He had gotten this from Galileo's writings, and Galileo had used this figure because that's what sailors of that time commonly used. Now, similar to the conflict between the calendars of Italy and England, they also used different definitions of a "mile". The Italian mile was 5000 feet, whereas the English mile was 5280 feet. Newton was aware of this difference, so he tried his calculation both ways, but it still gave a result for the Moon's orbit that implied an object at the Earth' surface should fall only 13.2 or 13.9 feet in one second, whereas Newton had measured that an object actually falls about 16.1 feet in one second at the Earth's surface.

According to William Whiston, "this made Sir Isaac suspect that this Power was partly gravity and partly that of Cartesius's Vortices", so he "threw aside the Paper of his Calculation and went on to other studies". Similarly, Henry Pemberton heard Newton say that "his [1666] computation did not answer his expectations, so he concluded that some other cause must at least join with the action of the power of gravity on the moon".

Not long afterwards, in 1670, the French astronomer Jean Picard determined with very accurate measurements that one degree of latitude equals 69.1 English miles. In 1675 this result appeared in the Royal Societies "Philosophical Transactions", and Newton saw it. He supposedly rushed home and excitedly repeated his earlier computation, this time finding it "perfectly agreeable to the Theory".

At least one prominent scholar has argued that Newton’s meditations in the 1660’s should not be regarded as “a moon test of the theory of gravitation”. No one disputes that Newton did indeed make calculations of the moon’s orbit, during which he inferred the inverse-square law, in the 1660’s, because the calculations were later found among his papers, written in the margins of a notebook in which Newton’s stepfather (Barnabas Smith) had compiled a glossary of theological terms. However, in the introductory guide to his modern English translation of the Principia, I. B. Cohen contends that these calculations cannot be seen as the origin of the theory of universal gravitation. His argument is that

The theory of gravitation is based on the central concept of a universal force. In the 1660s, Newton was considering something quite different, namely, a Cartesian endeavor, or "conatus," rather than a force, and certainly not a universal force. This endeavor was centrifugal, or directed outward, tending to produce an outward displacement, one having a direction away from the central body. Universal gravity is centripetal, directed inward, tending to produce an inward displacement.

I find this reasoning incomprehensible. A body moving in a circle exhibits an endeavor to recede from the center, because it’s inertial tendency is to diverge outward from the circular path. Admittedly, this endeavor can be (and has been) described in several different ways, such as in the modern definition of centrifugal force as a fictitious force with respect to a non-inertial system of coordinates. Cohen complains that “In the 1660s, Newton was still thinking of a centrifugal endeavor that had to be balanced so as to keep the body in orbit, in a kind of equilibrium”, but even in the final edition of the Principia, Newton uses the term in precisely this sense. (See the related note for a discussion of Newton’s uses of the term “centrifugal force” in the Principia.) It is a fact that the centrifugal endeavor of an orbiting body must be overcome and balanced by the centripetal force of gravity, noting that the word “endeavor” does not necessarily signify “force” in the modern sense. It might be more clear to refer to it as the “inertial endeavor”, and even in the modern literature the concept of inertial forces is widely used. Furthermore, regardless of whether this “endeavor to recede from the center” is regarded as a force or merely as an inertial endeavor to be counter-acted, it goes without saying that since the planets and the moon remain in their circular paths, their endeavors to recede are being counter-acted, and it is this counter-acting effect, directed toward the Earth (or the sun in the case of the planets) that Newton was identifying with the acceleration of gravity. In view of this, Cohen’s claim that Newton was discussing only an outward force is mystifying. Cohen concludes by saying that

Newton evidently did make a moon test of sorts in the 1660s. He evidently did conceive of gravity extending to the moon, but he certainly did not compare two "forces," one a "force requisite to keep the Moon in her Orb," the other the force of gravity. At this time, he did not as yet have the concept of such a "force," which he developed only a decade or so later, in the years before the writing of the Principia.

Admittedly the ultimate Newtonian concept of “force”, which Newton codified in the Principia, is not evident in his writings of the 1660’s, but it nevertheless seems clear (to me) that in his notes of the 1660’s Newton was doing precisely what Cohen is convinced he was not doing, namely, comparing the acceleration of the Earth’s gravity with the moon’s endeavor to recede from the Earth. In summary, by combining Kepler’s third law with Huygens’ expression for the “endeavor to recede from the center”, Newton saw that this endeavor (i.e., this tendency to diverge outwardly from the circular path) of the planets is inversely proportional to the square of the orbital radius. Since the planets remain in their circular paths, it isn’t difficult to suppose that, just as with objects moving in circles on Earth, some inward force is being applied to them. Now, the Earth has only one satellite, so it isn’t immediately obvious how to determine if Kepler’s law applies to satellites of the Earth. We know the moon’s endeavor to recede, and we know the radius of its orbit, but in order to test Kepler’s law we need to know what would be the endeavor to recede at some other radius.

We are on the Earth’s surface, at a radius of about 4000 miles from the Earth’s center, so we can ask, what would be the endeavor to recede of a satellite orbiting at this radius?  Suppose the force which keeps a satellite in its circular path, countering it’s endeavor to recede, is nothing other than gravity. On this supposition, the endeavor of a satellite at the Earth’s surface to recede must be equal in magnitude to the acceleration of gravity at the Earth’s surface, which we can measure directly. Newton’s calculations from the 1660’s show that the moon’s endeavor to recede is about 3600 times less than the acceleration of gravity at the Earth’s surface. Also, he noted that the moon is about 60 times further from the Earth’s center than is the surface of the Earth (using the more correct estimate for the Earth’s diameter). This shows consistency with three distinct bit inter-related hypotheses, first, that an analog of Kepler’s third law applies to satellites of all bodies, not just to satellites of the sun (which goes far towards understanding the universality of the phenomenon); second, that the force which counters the endeavor to recede of those satellites is to be identified with the gravity of the central body (universal gravitation); and third, that this force varies always as the reciprocal of the square of the distance from the center of the gravitating body. For example, from these considerations, it is an almost unavoidable conclusion that the planets are likewise maintained in their orbits by the gravitational attraction of the sun.

Of course, there is one serious objection to Newton’s reasoning. As Cohen rightly observes,

…in comparing the gravity on the surface of the earth with the force gravity would have at the moon, Newton assumed that the measure of the force was the inverse square of the distance from the center of the earth. Anyone who has read Section 12 of Book 1 of the Principia knows how difficult this was to prove.

We can go even further, and point out that (as discussed in the note on Newton’s Proposition LXXI) Newton himself said he strongly doubted the truth of this crucial proposition – until he found a proof of it. So, this is a valid and important caveat that must be placed on any claim that Newton knew or even had tested the law of universal gravitation in the 1660’s. However, this caveat has always been well known, and was fully acknowledge by Newton. As long as his reasoning relied on this unproven and frankly implausible-sounding  proposition, he knew that he was not in possession of a fully rationalized theory of gravity. On the other hand, we know that the proposition is actually true (as Newton later proved), so the early analyses based on that hypothesis can hardly be totally discounted. Also, notice that Cohen says Newton was “comparing the gravity on the surface of the earth with the force gravity would have at the moon”, which contradicts his (Cohen’s) fundamental thesis that Newton in the 1660’s considered only the endeavor to recede, not an inward force, and that he performed no comparison.

Incidentally, the two major aspects of Newton’s scientific work – namely, optics and mechanics – seems to have been associated with the two main astronomical bodies visible from the Earth. As noted above, the Moon apparently played an important role in his discovery of universal gravitation, and much of the Principia was devoted to determining the characteristics of the Moon's orbit. Newton is supposed to have said that his head never ached except for his studies of the Moon. That may be true, but he suffered some distress from the Sun as well, early in his career (in the prime of his age of invention), when he was studying optics. Indeed, one of the things that first interested Newton in optics was the phenomenon of "fantasy", which is the tendency to continue "seeing" a bright light for awhile after the light goes away, even if we close our eyes. To test this effect, Newton looked with one eye directly at the Sun for an extended period of time (!) until (as he reports in his notes) everything appeared either pale red or blue.

Then he went indoors, and after "ye motion of ye spirits in my eye were almost decayed" (i.e., normal vision was returning to the eye that had been exposed to the Sun), he closed that eye and, by imagining the Sun, found that the bright spot seemed to reappear to his vision. Then when he opened that eye he found that everything looked either red or blue again, i.e., the "spirits" of his eye had been stirred up again. Incredibly, he seems to have undertaken this experiment without considering the possibility of permanently damaging his eyesight. Only when the spots and optical "fantasies" persisted did he become worried, and he shut himself up in total darkness for several days before they finally subsided and his normal vision returned. It isn't clear if he told anyone what he had done, or if anyone noticed him sitting in his darkened rooms.

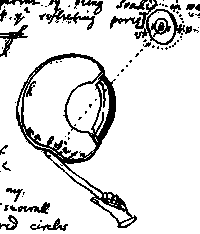
In his subsequent optical experiments Newton was more cautious about looking at direct sunlight, but he was still remarkably reckless in is treatment of his own eyes. For example, about a year later he wedged a blade "betwixt my eye and ye bone as near to ye back side of my eye as I could" to see the effects of deforming the retina. He even included a scary drawing of this experiment along with the written description in his notes.

These activities, combined with all the poisonous chemicals (like Mercury) that he inhaled during his chemical experiments, make it surprising that he lived in such good health to such an old age. It's reported that when he died at the age of 84 he still had all his teeth, which would be unusual even today.

Return to MathPages Main Menu