Intrinsic Wobble of Spinning Objects

It's known that the Earth's axis of spin is not perfectly aligned with its polar axis of symmetry, so it "wobbles" slightly. This wobble is not to be confused with the precession of the equinox, which is related to the fact that the Earth's axis of spin is tilted significantly with respect to its orbital plane around the Sun, and with respect to the Moon's orbital plane, which is a forced precession with a period of about 25,800 years.  In contrast, the wobble is just due to the free dynamics of the spinning Earth, due to the tilt between its angular momentum and it axis of symmetry. To analyze this kind of wobble in general, suppose we're given an axially symmetrical body with moment of inertia I₁ about the axis of symmetry and I₂ about each of the principal perpendicular axes. The body is floating freely in space, with no external forces, so we can take both the center of mass and the angular momentum vector H about that point to be fixed.

Let us define an orthogonal (and rotating) system of coordinates xyz with their origin at the center of mass, and such that the z axis is always pointing in the direction of the body's axis of symmetry, and the x axis is in the same plane as both the z axis and the angular momentum vector H.  The components of the angular momentum in the x, y, and z directions are then simply

where α is the angle between the z axis and H.  Also, since x, y, and z are the principal axes of inertia, we have

where ω_x, ω_y, and ω_z are the components of the total angular velocity ω of the body about the center of mass. Combining these relations gives

The component ω_y denotes the rate of change of α, and since this is zero, we see that the angle α remains constant, so the configuration  can only precess about the total angular momentum vector H. Furthermore, since ω_x/ω_z equals the tangent of the angle β between the z axis and the total angular velocity vector, it follows that

This suffices to give us a complete qualitative as well as quantitative picture of the motion.  Notice that the total angular velocity vector ω makes an angle β with the z axis, and it also makes an angle α−β with the total H vector.  Consequently, the vector ω sweeps out a "cone" about the fixed vector H, and it sweeps out another tangent cone about the rotating z axis (in accord with the well-known kinematical fact that the most general kind of free motion for a rigid body with a fixed point is generated by a "body cone" rolling on a "space cone").  The axis of the latter is the H vector, and the axis of the former is the z axis.  The line of tangency of these cones is the direction of the total angular velocity ω at each instant. 

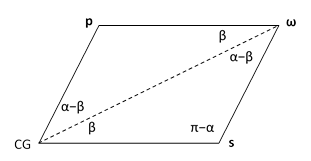
Also, notice that, depending on whether I₁ is less than or greater than I₂, the outside or inside surface of the body cone rolls around the outside of the space cone, giving forward or retrograde precession, respectively.  In either case, the relation between the total angular velocity ω, the relative spin rate s, and the free precession rate p can be inferred from the parallelogram

The law of sines immediately gives

Thus we have the free precession rate

and the relative spin rate

Using the trig identity sin(α−β) = sin(α)cos(β) − cos(α)sin(β) this reduces to

The relative spin rate s is the rate at which the angular velocity vector ω rotates, with respect to the body, about the body's axis of symmetry.  So, if we define this as the "rate of wobble", and if we recall that tan(β)/tan(α) = I₁/I₂, we get the well-known result that this rate equals 1 − I₁/I₂ times the projection of the angular velocity of the body onto the axis of symmetry (i.e., ω_z).  For the Earth we have I₁/I₂ = 1.0033, so the free precession is retrograde, i.e., the angular velocity vector ω rotates in a cone in direction opposite the direction of ω_z.  We have s = −0.0033 ω_z, so the period is about 303 days (since ω_z has a period of about 1 "day").

It turns out that the actual observed period of this precession is substantially longer, about 432.5 mean solar days.  This differs from our computed value mainly because we assumed an ideal rigid body, whereas the Earth is not perfectly rigid.

Return to MathPages Main Menu