Platonic Solids and Plato's Theory of Everything

The Socratic tradition was not particularly congenial to mathematics, as may be gathered from Socrates' inability to convince himself that 1 plus 1 equals 2, but it seems that his student Plato gained an appreciation for mathematics after a series of conversations with his friend Archytas in 388 BC. One of the things that most caught Plato's imagination was the existence and uniqueness of what are now called the five "Platonic solids". It's uncertain who first described all five of these shapes - it may have been the early Pythagoreans - but some sources (including Euclid) indicate that Theaetetus (another friend of Plato's) wrote the first complete account of the five regular solids. Presumably this formed the basis of the constructions of the Platonic solids that constitute the concluding Book XIII of Euclid's Elements. In any case, Plato was mightily impressed by these five definite shapes that constitute the only perfectly symmetrical arrangements of a set of (non-planar) points in space, and late in life he expounded a complete "theory of everything", in the treatise called Timaeus, based explicitly on these five solids. Interestingly, almost 2000 years later, Johannes Kepler was similarly fascinated by these five shapes, and developed his own cosmology from them.

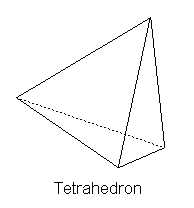
To achieve perfect symmetry between the vertices, it's clear that each face of a regular polyhedron must be a regular polygon, and all the faces must be identical. So, Theaetetus first considered what solids could be constructed with only equilateral triangle faces. If only two triangles meet at a vertex, they must obviously be co-planar, so to make a solid we must have at least three triangles meeting at each vertex. Obviously when we have arranged three equilateral triangles in this way, their bases form another equilateral triangle, so we have a completely symmetrical solid figure with four faces, called the tetrahedron, illustrated below.

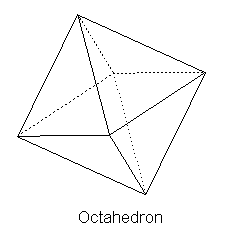
On the other hand, if we make four triangles meet at a vertex, we produce a square-bottomed pyramid, and we can obviously put two of these together, base to base, to give a completely symmetrical arrangement of eight triangular faces, called the octahedron, shown below.

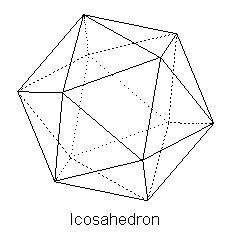
Next, we can make five equilateral triangles meet at a point. It's less obvious in this case, but if we continue this pattern, adding equilateral triangles so that five meet at each vertex, we arrive at a complete solid with 20 triangular faces. This is called the icosahedron, shown below.

Now, we might try putting six equilateral triangles together at a point, but the result is a planar arrangement of triangles, so it doesn't give a finite solid. I suppose we could regard this as a Platonic solid with an infinite radius, which might have been useful in Plato's cosmology, but it doesn't seem to have been viewed this way. Perhaps this is not surprising, considering the well-known aversion of the ancient Greek mathematicians to the complete infinity. In any case, we clearly can't construct any more perfectly symmetrical solids with equilateral triangle faces, so we must turn to other possible face shapes.

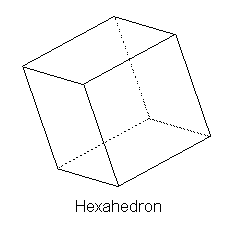
The next regular polygon shape is the square, and again we find that putting just two squares together does not yield a solid angle, so we need at least three squares to meet at each vertex. Putting three squares together we see that we can add three more to give the perfect solid with six faces, called the hexahedron (also known as the cube). This is shown below.

If we try to make four square faces meet at each vertex, we have another plane surface (giving another "infinite Platonic solid"), so clearly this is the only finite perfectly symmetrical solid with square faces.

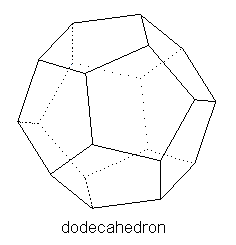
Proceeding to pentagonal (five-sided) faces, we find that if we put together 12 pentagons so that three meet at each vertex, we arrive at the fifth Platonic solid, called the dodecahedron, illustrated below.

It isn't self-evident that 12 identical regular pentagons would come together perfectly like this to form a closed solid, but it works, as Theaetetus proved and as Euclid demonstrates at the conclusion of The Elements. Of course, if we accept that the icosahedron works, then the dodecahedron automatically follows, because these two shapes are "duals" of each other. This means that the icosahedron has 20 faces and 12 vertices, whereas the dodecahedron has 12 faces and 20 vertices, and the angular positions of the face centers of one match up with the positions of the vertices of the other. Thus, once we have the icosahedron, we can just put a dot in the center of each face, connect the dots, and viola!, we have a dodecahedron. Similarly, the cube and the octahedron are duals of each other. Also, the tetrahedron is the dual of itself (so to speak).

Clearly it's impossible for four (or more) pentagonal faces to meet at a vertex, because they subtend more than 360 degrees. For hexagonal (six-sided) faces, three hexagons meeting at a point constitute another "infinite solid", i.e., a planar surface. It's also obvious that no higher-order polygon can yield a solid, so the five solids already mentioned - tetrahedron, hexahedron, octahedron, icosahedron, and dodecahedron - are the only regular polyhedrons. Theaetetus not only proved that these solids exist, and that they are the only perfectly symmetrical solids, he also gave the actual ratios of the edge lengths E to the diameters D of the circumscribing spheres for each of these solids. This is summarized in Propositions 13 through 17 of Euclid's Elements.

In Timaeus, Plato actually chose to constitute each of these solids from right triangles, which played the role of the "sub-atomic particles" in his theory of everything. In turn, these triangular particles consisted of the three legs (which we might liken to quarks), but these legs were ordinarily never separated. The right triangles that he chose as his basis particles were of two types. One is the "1,1," isosceles triangle formed by cutting a square in half, and the other is the "1,2," triangle formed by cutting an equilateral triangle in half. He used these to construct the faces of the first four solids, but oddly enough he didn't just put two together, he used six "1,2, triangles to make a triangular face, and four "1,1," triangles to make a square face, as shown below.

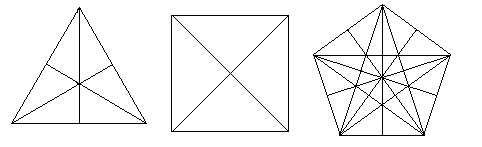
Of course, it's not possible to build a pentagon from these two basic kinds of right triangles, and Plato doesn't actually elaborate on how the faces of the dodecahedron are to be constructed, but from other sources we know that he thought each face should be composed of 30 right triangles, probably as shown on the right-hand figure above, so that the dodecahedron consisted of 360 triangles. The tetrahedron, octahedron, and icosahedron consisted of 24, 48, and 120 triangles (of the type 1,2,), respectively, and the hexahedron consisted of 24 triangles (of the type 1,1,).

Now, if the basic triangles were the subatomic particles, Plato regarded the solids as the "atoms" or corpuscles of the various forms of substance. In particular, he made the following identifications

The idea that all the constituents of nature consist of mixtures of a small number of "elements", and in particular the selection of the four elements of earth, water, air, and fire, is attributed to an earlier Greek philosopher Empedocles of Agrigentum (495-435 BC). Empedocles believed that although these elements (which he called "the roots of all things") could be mixed together in various proportions, the elements themselves were inviolable, and could never be changed. In contrast, one of the intriguing aspects of Plato's theory was that he believed it was possible for the subatomic particles to split up and re-combine into other kinds of atoms. For example, he believed that a corpuscle of liquid, consisting of 120 "type 1" triangles, could be broken up into five corpuscles of plasma, or into two corpuscles of gas and one of plasma. Also, he believed that the "smaller" corpuscles could merge into larger corpuscles, so that (for example) two atoms of plasma could merge and form a single atom of gas. However, since the basic triangles making up "earth" (cubes) are dissimilar to those of the other forms of substance, he held that the triangles comprising cubes cannot be combined into any of the other shapes. If a particle of earth happened to be broken up into its constituent triangles, they will "drift about - whether the breaking up within fire itself, or within a mass of air or water - until its parts meet again somewhere, refit themselves together and become earth again".

When Plato asserts that the [1,1,] triangles cannot combine into anything other than a cube, it's conceivable that he was basing this on something more that just the geometric dissimilarity between this triangle and the [1,2,] triangle. He might also have had in mind some notion of the incommensurability of the magnitudes  and , not only with the unit 1, but with each other. Indeed the same Theaetetus who gave the first complete account of the five "Platonic" solids is also remembered for recognizing the general fact that the square root of any non-square integer is irrational, which is to say, incommensurable with the unit 1. It isn't clear whether Theaetetus (or Plato) knew that two square roots such as  and  are also incommensurable with each other, but Karl Popper (in his anti-Plato polemic "The Free Society and its Enemies") speculated that this might have been known, and that Plato's choice of these two triangles as the basic components of his theory was an attempt to provide a basis (in the mathematical sense) for all possible numbers. In other words, Popper's idea is that Plato tentatively thought the numbers 1, , and  are all mutually incommensurable, but that it might be possible to construct all other numbers, including , π, etc., as rational functions of these.

Of course, Book X of Euclid's Elements (cf. Prop 42) dashes this hope, but it's possible that the propositions recorded there were developed subsequent to Plato's time. Popper also makes much of the numerical coincidence that + is approximately equal to π, and speculates that Plato might have thought these numbers were exactly equal, but this doesn't seem credible to me. For one thing, it would give a means of squaring the circle, which would certainly have been mentioned if anyone had believed it. More importantly, the basic insight of Theaetetus was in recognizing the symmetry of all the infinitely many irrational square roots, and it just doesn't seem likely that he (or Plato) would have been misled into supposing that just two of them (along with the unit 1) could form the basis for all the others. It's a very unnatural idea, one that would not be likely to occur to a mathematician. (Still, an imaginative interpreter could probably discern correspondences between the four basis vectors of "The Platonic Field", i.e., numbers of the form A + B+ C + D and Plato's four elements, not to mention the components of Hamilton's quaternions.)

It's also interesting that Plato describes the "1,1," triangle as the most "stable", and the most likely to hold its shape, thus accounting for the inert and unchanging quality of the solid elements. He didn't elaborate on his criterion for "stability", although we can imagine that he had in mind the more nearly equal lengths of the edges, being closer to equilibrium. On the other hand, this would suggest that the equilateral triangle (which is the face of Plato's "less stable" elements) was highly stable. Plato made no mention of the fact that the cube is actually the only unstable Platonic solid, in the sense of rigidity of its edge structure. In addition, the cube is the only Platonic solid that is not an equilibrium configuration for its vertices on the surface of a sphere with respect to an inverse-square repulsion. Nevertheless, the idea of stability of the sub-atomic structure of solid is somewhat akin to modern accounts of the stability of inert elements.

We can also discern echoes of Plato's descriptions in Isaac Newton's corpuscular theory. Newton's comments about the "sides" of light particles are very reminiscent of Plato's language in Timaeus. It's also interesting to compare some passages in Timaeus, such as

And so all these things were taken in hand, their natures being determined by necessity in the way we've described,  by the craftsman of the most perfect and excellent among things that come to be...

with phrases in Newton's Principia, such as

...All the diversity of created things, each in its place and time, could only have arisen from the ideas and the will of a necessarily existing being...

...all phenomena may depend on certain forces by which the particles of bodies...either are impelled toward one another and cohere in regular figures, or are repelled from one  another and recede...

...if anyone could work with perfect exactness, he would be the most perfect mechanic of all...

Plato explicitly addressed the role of necessity in the design of the universe (so well exemplified by the five and only five Platonic solids), much as Einstein always said that what really interested him was whether God had any choice in the creation of the world. But Plato was not naive. He wrote

Although [God] did make use of the relevant auxiliary causes, it was he himself who gave their fair design to all that comes to be. That is why we must distinguish two forms of cause, the divine and the necessary. First, the divine, for which we must search in all things if we are to gain a life of happiness to the extent that our nature allows, and second, the necessary, for which we must search for the sake of the divine. Our reason is that without the necessary, those other objects, about which we are serious, cannot on their own be discerned, and hence cannot be comprehended or partaken of in any other way.

The fifth element, i.e., the quintessence, according to Plato was identified with the dodecahedron. He says simply "God used this solid for the whole universe, embroidering figures on it". So, I suppose it's a good thing that the right triangles comprising this quintessence are incommensurate with those of the other four elements, since we certainly wouldn't want the quintessence of the universe to start transmuting into the baser substances contained within itself!

Timaeus contains a very detailed discussion of virtually all aspects of physical existence, including biology, cosmology, geography, chemistry, physics, psychological perceptions, etc., all expressed in terms of these four basic elements and their transmutations from one into another by means of the constituent triangles being broken apart and re-assembled into other forms. Overall it's a very interesting and impressive theory, and strikingly similar in its combinatorial (and numerological) aspects to some modern speculative "theories of everything", as well as expressing ideas that have obvious counterparts in the modern theory of chemistry and the period table of elements, and so on.

Timaeus concludes

And so now we may say that our account of the universe has  reached its conclusion. This world of ours has received and  teems with living things, mortal and immortal. A visible  living thing containing visible things, and a perceptible God, the image of the intelligible Living Thing. Its grandness,  goodness, beauty and perfection are unexcelled. Our one  universe, indeed, the only one of its kind, has come to be.

The speculative details of Plato's "account of the universe" are not very satisfactory from the modern point of view, but there's no doubt that - at least in its scope and ambition as an attempt to represent "all that is" in terms of a small number of simple mathematical operations - Plato's "theory of everything" left a lasting impression on Western science.

Return to MathPages Main Menu