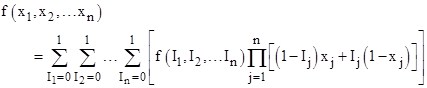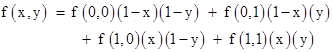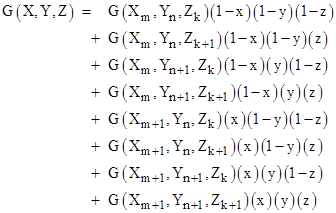Boolean Expansion as Linear Interpolation

Given a set of n independent logical variables X₁, X₂, ..., X_n, each of which may be either TRUE or FALSE, let x_j = P{X_j} denote the probability that X_j is TRUE. Consequently 1 − x_j is the probability that X_j is FALSE.

Now consider some arbitrary Boolean function F(X₁, X₂, ..., X_n) of these n logical variables.  Thus for any specified truth values of the n variables the function F is assigned a particular value, either TRUE or FALSE.  In his "Investigation of the Laws of Thought" George Boole described (Chapter V, Prop II) how the probability f of the function F can be expanded into its mutually exclusive components. This expansion is just an application of the conditional probability formula for an arbitrary event E and logical variable X

where an overbar signifies logical negation, and the vertical line "|" signifies "given". Applying this repeatedly to the event F and the logical variables X_j with probabilities x_j gives the expansion formula

where the indices I_j, j=1,2,..,n signify truth values (0=FALSE, 1=TRUE).

For example, given a Boolean function F of two independent logical variables X and Y whose probabilities of being TRUE are x and y respectively, we can express the function f(x,y) = P{F(X,Y)} as follows

In this formula the expression f(0,0) is the probability of F(X,Y) given that X and Y are both FALSE, and similarly f(0,1) is the probability given that X is FALSE and Y is TRUE, and so on.

It's interesting that the general formula for Boolean decomposition of probabilities in terms of n independent variables is identical to the formula for n-dimensional orthogonal linear interpolation. Suppose we have an orthogonal n-dimensional table that specifies the value of a scalar field f(x₁, x₂, ..., x_n) at discrete points. To interpolate the value of f at some specific point in this n-dimensional space using linear interpolation, we need to first find the particular "cell" of the table where the point falls. Once we have done this, we can normalize the spatial coordinates along each axis such that the next lower table ordinate is 0 and the next higher table ordinate is 1. Then the values of f(I₁, I₂,..., I_n) in the above general formula for the Boolean expansion represent the discrete table values at the 2ⁿ vertices of the relevant "cell" of the table, and the values of x_j for j=1 to n are the spatial coordinates of the particular point inside the cell that is to be interpolated.

For an explicit example of practical interpolation, suppose we have a three-dimensional orthogonal table giving discrete values of some real-valued function G(X,Y,Z), and we want to interpolate the value for some specific values of X, Y, and Z within the range of the table node values X_m to X_m+1, Y_n to Y_n+1, and Z_k to Z_k+1. We first define the normalized parameters

The interpolated value is then given by

The correspondence between interpolation in a Euclidean space and the expansion of the probabilities of logical functions suggests some interesting approaches to dealing with more challenging situations in which the logical variables are not independent. We can express these in terms of the non-independence of a putative set of "basis vectors" for the space. However, it's important to keep in mind that the general locus given by n-dimensional linear interpolation actually possesses intrinsic curvature, and isn't linear with respect to arbitrary independent basis vectors. For a discussion of this intrinsic curvature, see Curvature of Linear Interpolation.

Return to MathPages Main Menu