Mayan Numeration

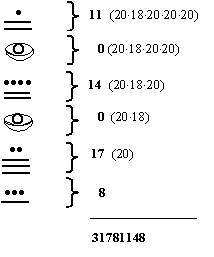
The pre-Columbian Mayans developed a fairly sophisticated system of numeration, primarily for the purpose of making calendars and keeping  track of time.  (A concern for quantifying the passage of time, and minding the calendar, seems to have been a characteristic of many primitive peoples, and prompted much of the early record-keeping.) An example of a Mayan representation of a number is shown below:

The Mayans wrote their numbers vertically, with each "digit" being represented by either a set of dots and horizontal lines or else a symbol that looks (to me) like an empty bowl, which denotes zero (an impressive invention of the Mayans, considering how many millennia it took the people of the other hemisphere to think of it).  For the  non-zero digits, each horizontal dash represents 5, and each dot  represents 1, and these are simply added together to give the value of the digit.  Thus each non-zero digit consists of from 0 to 4 dots,  and from 0 to 3 lines, and these arrangements, along with the "empty  bowl", give representations for every number from 0 to 19. 

Then they used a "place" system (another impressive invention), with  the lowest digit signifying 1's, and the higher places signifying  more powers of the base which was nominally always 20.  However, the  system had one anomaly in that the denomination increased by a factor of 18 instead of 20 when rising from the second to the third digit. The presumed explanation for this is simply that since the Mayans were mainly interested is counting days, and their basic annual calendar had 360 days, it was most convenient for the denomination of the 3rd least significant digit to be (20)(18) = 360 instead of (20)(20) = 400.

Of course, one consequence of this anomaly is that the possible representations of a given number are not necessarily unique.  For example, suppose we tip the Mayan numbers over, so the digits are horizontally arrayed, and we use our numerals to signify the digit. Then the decimal number 360 could be represented in the Mayan system as either  (1 0 0)  or as  (18 0).  A nice feature of our more conventional fixed-base representations is that they give a strict one-to-one correspondence between the natural numbers and all the possible permutations of a fixed set of digits.

For some reason the "18-anomaly" in Mayan numeration reminds me of a funny story that Isak Dinesen told in her autobiographical book "Out of Africa".  When she first arrived in Africa from her native Denmark she was sent to a "shy young Swedish dairy-man" who was to teach her the Swaheli number system.  Now, it so happens that the Swaheli word for "nine" is very difficult for a Swede to pronounce, so when teaching the numbers this dairy-man invariably skipped it, explaining the omission by telling her that the Swaheli "have not got nine".  "Does that work?" asked the Baroness.  "What do they do when they come to nineteen?"

“They have not got nineteen either" he said, blushing, but very firm. "Nor ninety, nor nine-hundred" - for these words in Swaheli are constructed out of the number nine - "But apart from that they have got all our numbers.”  The idea of this system for a long time gave me much to think of, and for some reason a great pleasure.  Here, I thought, was a people who have got originality of mind, and courage to break with the pedantry of the numeral series..."

She went on to describe some interesting ideas that were prompted by the alleged absence of "nine" from the number system.  Just as two and three are the only consecutive prime numbers, so (she thought) we might regard eight and ten as the only consecutive even numbers (apparently forgetting about 18 and 20).  She then noted that people  might try to prove the existence of "nine" by arguing that it should  be possible to multiply "three" by itself, but she points out that the number "two" has no square root [among the integers], so why should we insist that the number "three" have a square?  It isn't clear if she  knew that the square root of two is irrational, but in any case her  point is valid: the elements contained within any given set of numbers need not include all conceivable numbers based on arithmetic operations involving those elements.

She then makes the interesting observation that

If you work out the sum of digits of a number until reducing it to a single figure, it makes no difference to the results if you have got the number of nine, or any multiple of nine, in it from the beginning, so that here nine may really be said to be non-existent, and that, I thought, spoke for the Swaheli system.

Setting aside the question of whether this arithmetical fact (in the decimal number system) implies the "non-existence" of the number nine, or whether the Swaheli even used a decimal number system, I  find it interesting that the Baroness Blixen was familiar with  this arcane bit of numerical trivia.  I suppose the process of  "casting out nines" was better known in the days when all  computations were performed by hand... speaking of which, she also mentioned that one of her servant boys at the time was missing the  fourth finger of his left hand.  "Perhaps, I thought, this is a  common thing with Natives, and is done to facilitate their arithmetic to them, when they are counting upon their fingers."

Alas, all these engaging ideas had to be abandoned when she learned  that the Swaheli actually do have the number nine, and her Swedish  tutor had just been unable to pronounce it.  If he thought this omission would make no difference to his pupil, he obviously misjudged her. Even after being enlightened as to the Swaheli nine, Karen's original idea retained its romantic appeal for her.

Yet I still have got the feeling that there exists a Native system of numeral characters without the number nine in it, which to them works well and by which you can find out many things.

Sometimes a simple act of counting can signify, for the artistic mind, more than just an abstract quantification.  From Eliot's "The  Waste Land":

Who is the third who walks always beside you?

When I count there are only you and I together

But when I look ahead up the white road

There is always another one walking beside you

Gliding wrapt in a brown mantle, hooded

I do not know whether a man or a woman

-But who is that on the other side of you?

In his notes to the poem, Eliot explained

The ... lines were stimulated by the account of one of the Antarctic expeditions (I forget which one, but I think one of Shackleton's): it was related that the party of explorers, at the extremity of their strength, had the constant delusion that there was one more member than could actually be counted.

Return to MathPages Main Menu