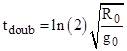Gravity as Expansion and Many Worlds

Each point on the Earth’s surface is accelerating upward at a rate of 9.8 m/sec² in terms of the local free-falling system of inertial coordinates. When people first learn this fact, they sometimes entertain (for a moment) the idea of the Earth as an expanding sphere, with a radius increasing at a constantly accelerating rate. In fact, since all matter evidently gravitates, we might image that all matter is expanding at an accelerating rate. Of course, material objects like the Earth don’t seem to be getting any larger, but we might account for this by imagining that the size of every object (and the spatial characteristic of every physical phenomenon) is increasing in proportion to the Earth’s radius, so there is no comparative basis for discerning an increase. According to this simple model, gravitation is not a force of attraction, it is ordinary inertia in the context of continually expanding matter.

Most people briefly ponder this idea at an early age, but discard it when they notice the many ways in which it is inconsistent with the known phenomena of gravity. For example, the expansion interpretation would imply that the acceleration of gravity is strictly dependent only on the size of an object, rather than on it’s mass (or else that objects are expanding at disproportionate rates, so their relative sizes change drastically). Also, the expansion interpretation would imply that the acceleration of gravity is independent of distance, rather than varying inversely as the square of the distance. Thus the two most salient features of gravitational acceleration – being proportional to mass and inversely proportional to the square of the distance – are both inconsistent with the expansion interpretation. In addition, it’s clear that orbital motion cannot be accounted for in terms of purely radial expansion of massive objects (as discussed below). Also, the fact that the acceleration of gravity is actually greater at the bottom of a mine shaft than at the Earth’s surface (due to relatively less dense material in the Earth’s outer layers) is obviously impossible to reconcile with an expansion model. It implies that the interior sphere is continually expanding more rapidly then the enclosing exterior shell. Likewise the expansion model predicts that a test particle inside a spherical shell of matter would appear to be attracted toward the center of the shell (as the shell expands), whereas in fact there is no gravitational acceleration at all in the interior of a spherical shell of matter. Needless to say, although the expansion model is conceived as satisfying the principle of equivalence, it does not entail any time dilation, and therefore does not predict any gravitational redshift, so it actually contradicts the strong equivalence principle.

As an aside, the expansion model may have its psychological origin in the conception of the world that humans dimly recall from their infancy. When looking at the world from his crib, a toddler doesn’t see a spherical Earth in orbit around the sun, nor the gravitational accelerations between every pair of material objects, proportional to the products of their masses and inversely proportional to their distances. Instead, he sees a simple flat world in which the only discernible manifestation of gravity is the tendency of all objects to accelerate “downward” at the same rate. Within this infantile model of the world, one can indeed save all the discernible phenomena by supposing that the flat ground is actually accelerating “upward” at a constant rate. (Admittedly this implies the expenditure of a stupendous amount of work, but the infant knows nothing of conservation of energy.) This primitive “theory of relativity” asserts that the apparent downward acceleration of all objects can be “explained” by the upward acceleration of the (infinite flat) ground. There is no question of mass dependence in this infantile world, because there is only one acceleration involved in gravity, namely, the upward acceleration of “the ground”. Also there is no question of inverse-square effects, because the infant’s experience is entirely confined to a region in which the acceleration of gravity is constant. Furthermore, in this world there are no orbital motions, tidal effects, or any of the other phenomena of actual gravitation. Of course, this infantile view breaks completely down as soon as we acquire more knowledge of the real world.

Despite the fact that the expansion interpretation of gravity is grossly inconsistent with even the most commonplace phenomena of gravity, it is nevertheless the only model, aside from the curvature interpretation of general relativity (and associated metrical theories of gravity), in which the equivalence principle is literally valid and occurs as a natural feature. According to the expansion interpretation, just as for the passive response of particles in general relativity, there is no “force” of gravity per se. Rather, all free test particles are considered to follow inertial paths. In both theories, kinetic acceleration and gravitational acceleration are literally the same thing. Nevertheless, while general relativity incorporates the equivalence principle within a conceptually clear and empirically successful theory of gravity, the expansion interpretation fails utterly. It’s interesting to examine the expansion interpretation in some detail, to understand exactly why it doesn’t lead to a viable conception of gravity. We will argue that there’s a very close parallel between the expansion interpretation of gravity and the many-worlds interpretation of quantum mechanics, and that both of these interpretations are inadequate for quite analogous reasons.

First, it’s necessary to address an inherent ambiguity in the expansion interpretation of gravity. To account for the fact that objects don’t appear to be increasing in size, we were forced to stipulate that all “objects” are increasing their spatial extents in a fixed proportion to each other. (The fact that they must all expand in the same proportion leads to the inconsistency with the mass dependence, but we set that aside for the moment.) However, we must then decide what constitutes an “object”. If we were to assume every spatial extent is somehow increased in a certain proportion, we would defeat the original purpose of the posited expansion, which was to explain why (for example) a rock dropped off a bridge appears to fall to the river below. The original idea of the expansion model of gravity is that the rock does not actually accelerate when released (because there is no pull of gravity) but rather the surface of the Earth accelerates upward to meet it, but if we assumed the distance from the rock to the river was also increasing in proportion to the Earth’s radius, then the Earth would never approach the rock, so the rock wouldn’t seem to fall. Therefore, we cannot posit that all spatial extents are automatically increasing. In other words, if we are to account for the phenomena of gravity, we must assume that some spatial extents are naturally expanding (for some unspecified reason) and some are not. But then we must answer the question of what determines whether or not a given spatial extent is naturally increasing.

It might seem as if this could be answered by simply postulating that the spatial extensions of “solid” material objects are automatically increasing, while the spatial distances between material objects are not. However, this is not a viable explanation, because we know all “solid objects” (including the Earth) are mostly empty space. The actual nucleons and electrons comprising a solid object make up only a tiny fraction of the object’s volume. If we assume only solid bodies (or aggregates of solid bodies in direct contact with each other) automatically expand, while the distances between them do not, we are forced to conclude that the distances between elementary particles must shrink to zero almost immediately, and this must occur prior to any expansion of the overall Earth. The same problem applies to the stars in the galaxy if we regard individual stars as “solid objects”, but not the overall galaxy. If the stars are increasing in size but the distances between them are not increasing, then the stars will very quickly collide with each other. So the simple notion of expanding matter as the cause of gravity is incompatible with the known structure of matter, both at the smallest scales and the largest. If the problem were only on a small scale, we might postulate that the electromagnetic and nuclear forces maintaining the shapes of solid material objects somehow compel expansion, but this cannot account for large-scale configurations of matter (like galaxies), unless we postulate that the distances between stars naturally expand, but this (again) defeats the purpose of expansion, since there would be no tendency for bodies to converge.

One amusing side note on the expansion model of gravity is that it implies the rate of expansion must actually be exponential, because the effective acceleration must always be in terms of the current scaling, which is changing constantly as objects expand. For example, when we say the surface of the Earth is accelerating upward at 9.8 m/sec², this refers to meters as measured by rulers which are expanding in proportion to the expanding Earth. Thus in terms of the true inertial measures, the radius R of the Earth must be expanding at a fixed percentage of the current radius per square second. To be precise, the radius must satisfy the relation d²R/dt² = (g₀/R₀)R, where g₀ is the acceleration of gravity at the Earth’s surface in terms of rulers, and R₀ is the measured radius at some arbitrary initial instant. As a result, we have

The measured radius of the Earth is about (6.36)10⁶ meters, so the actual radius of the Earth must double every 9.3 minutes. In general, the doubling time required for an a sphere of radius R0 to have a gravitational acceleration of g0 on its surface is

Since the ration of R₀ to g₀ is different for different objects (the Earth happens to have the lowest value of this ratio for any body in the solar system), this contradicts the fact that all objects would need to double in exactly the same amount of time to maintain the same proportional sizes. Of course, it also shows that the actual acceleration of gravity must double every 9.3 minutes... all of which is completely contrary to the facts. (Needless to say, any attempt to repair some of these defects by postulating a change in the rate of passage of time would be self-defeating, since the same reasoning applies to whatever measure of time is regarded as the true time.) Noting that the acceleration of gravity at the surface of a sphere of radius R₀ and mean density ρ is GM/R₀² where G is Newton’s constant and M equals (4/3)πR³ρ, we have

Therefore the time for any object to double in size is dependent on the mean density of the object. Since the mean densities of other objects (such as the Sun and Moon) are less than that of the Earth, their sizes in proportion to the Earth must be continually shrinking, becoming microscopic within the time of a single day. For example, to account for the acceleration of gravity on the Moon, applying the same analysis as for the Earth, we find that the Moon must double in size every 11.9 minutes, which means that in any single day the size of the Moon doubles 121 times, whereas the size of the Earth doubles 154 times, so after just one day the Earth is eight billion times larger than the Moon. Likewise a gold sphere would expand more rapidly than a wooden sphere of the same initial size. All of these predictions of the expansion model are obviously absurd. Of course, it also fails to yield the inverse-square dependence of acceleration with distance, as can easily be seen by considering an object nearly stationary far from a single gravitating body.

We also note that perfectly spherical objects are the only ones that would be maintain their shapes under this kind of expansion, because the acceleration of gravity on the surface of non-spherical objects varies from one part of the surface to another, so the expansion would occur at different rates, resulting in drastic changes in the shapes of ordinary objects.

There is no self-consistent resolution for the problems inherent in the expansion interpretation, so any effort to examine the consequences of this interpretation must proceed on a purely ad hoc basis, treating each situation opportunistically by assigning automatic expansion to some elements of the situation while assuming that other spatial extents are behaving in accord with normal inertial kinematics. (Needless to say, if we were to reject ordinary inertia, the entire basis for the explanation of the acceleration of gravity in terms of expansion would be rejected along with it.) Clearly this is not a serious scientific theory, but it’s still interesting to examine some aspects of the interpretation, particularly the problem of orbits.

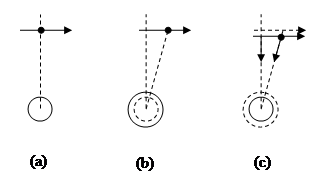
The curved spacetime interpretation of gravity (i.e., general relativity) differs from the simplistic expansion interpretation fundamentally in that the former acknowledges actual influence of spatially separate bodies on each other (via the gravitational field), whereas the latter does not. To illustrate this difference, consider a small test particle passing near a large gravitating body as illustrated below.

According to the expansion interpretation, during the time between figures (a) and (b) the test particle moves slightly to the right along its inertial path, and the gravitating body expands by some amount, due to the (unexplained) natural expansion of material bodies. The crucial step then occurs between figures (b) and (c), where we essentially “rescale” our perceptions of the magnitudes of spatial extents, due to the presumed fact that all rulers and other comparatives measures have expanded in exact proportion to the expansion of the gravitating body. But the question arises as to how precisely we are supposed to carry out this “rescaling” of our perceptions. Suppose we simply choose a convenient point, say, the center of the gravitating body, to remain fixed in position, and we then radially reduce all distances from that point by the same factor. This has the apparent effect of moving the test particle closer to the gravitating body, but of course it also moves the previous location of the test particle closer to the gravitating body. (We could make this explicit by imagining a sequence of test particles all moving in a line.) Therefore, the trajectory of the test particle has not changed direction as a result of the re-scaling, so the test particle is still moving directly to the right. This will continue to be the case for all subsequent times, so if the test particle was over the “north pole” in figure (a) it can never be over a point below the “equator” of the gravitating body.

This is an unavoidable feature of the expansion interpretation, because it is based on the premise that the center of mass of each object moves inertially unless it comes into direct contact with some other object. An orbiting test particle never comes into direct contact with the gravitating body, so it must continue to move uniformly in a straight line, and hence cannot circle completely around an object, regardless of how the radial scaling is altered. Now, it might be suggested that the contraction phase (i.e., the re-scaling) is to be regarded as an actual physical effect, changing the direction of motion of the test particle, but this clearly violates the basic premise of the expansion interpretation, which is to deny any actual influence “at a distance”. Furthermore, if we were to regard the effects of re-scaling as actual motions, then the choice of the center of contraction is no longer arbitrary, and the distances through which objects move when the re-scaling takes place are unbounded. For example, if we take the center of the galaxy as the center of contraction, and re-scale all distances in proportion to their distances from the center of the galaxy, then this would imply huge changes in the trajectories of objects occurring continuously.

The only potentially viable alternative is to postulate that there are different “centers of contraction” in different regions of space, presumably concentrated in regions of high mass content. If we also stipulate that these contractions are real rather than just perceptual, i.e., if we stipulate that the contractions actually change the paths of objects, even if those objects are not in direct contact with any other objects, then we have an effective field theory of influence at a distance, which is precisely what the expansion interpretation was intended to obviate. Also, since these real physical contractions of the local inertial metric of space and time must be continuously countering the expansion, it follows that there is no expansion. The only actual process taking place is that the local metric of space and time in the vicinity of massive bodies is curved in such a way that the inertial free-fall frames are accelerating inward at a rate proportional to the mass and inversely proportional to the square of the distance.

Thus, beginning with the naïve idea of physical expansion as the cause of gravity, we are compelled step-by-step to the conclusion that the effective metric of spacetime must be contracting around massive bodies. If we examine in detail the requirement for the surface of an object to be accelerating outward in terms of the local inertial frames, even though the surface itself is stationary, we find that this “accelerating in place” implies that space is curved in time, and the rate of proper time is lower near massive bodies. This leads to the curved spacetime interpretation of general relativity, which of course gives a very satisfactory representation of all known gravitational phenomena.

We mentioned in the introduction an analogy with the many-worlds interpretation of quantum mechanics. Recall that the many-worlds, or, more generally, the no-collapse, interpretations of quantum mechanics postulate that the universe evolves in accord with the linear Schrödinger equation, and there is no actual “collapse of the wave function”. It simply continues to evolve, expanding into an ever enlarging space of universes. Of course, just as the expansion interpretation of gravity needs to account for the fact that things don’t seem to be expanding, so the “no-collapse” interpretations of quantum mechanics need to explain why we don’t seem to be evolving into proliferating superpositions of universes. In both cases, the notion of actual contraction of space or actual collapse of the wave function is considered to be objectionable, and it is claimed that we can simply dispense with these operations, and explain the contrary appearances as purely perceptual. In the case of expansion interpretation of gravity, we are asked to believe that somehow our perceptions of scale are continuously being adjusted, and that this somehow produces the real appearance of orbits and all the other phenomena of gravity. Likewise in the case of no-collapse interpretation of quantum mechanics we are asked to believe that somehow our perceptions single out one particular branch of the proliferating universes, so that the world seems to exhibit a unique history.

Both of these “no collapse” theories suffer from the same fundamental problem, which is that they attempt to explain real physical effects as merely artifacts of perception, and yet they fail to provide a plausible account of how the actual observed phenomena can be represented purely in terms of perception. Occasionally the proponents of no-collapse interpretations of quantum mechanics appeal to some yet-to-be-defined theory of consciousness, in terms of which everything will make sense. If there were any serious proponents of the expansion interpretation of gravity, they could presumably make the same appeal. However, physical theories that can claim to make sense only in the context of some presently undefined theory of consciousness are inherently dubious. Also, the example of general relativity shows that it is sometimes possible to achieve a more profound understanding by actually addressing the phenomena within the context of our present consciousness.

Return to MathPages Main Menu