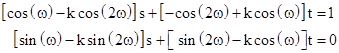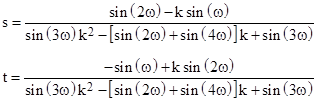Cutting Self-Similar Pentagons

Is it possible to cut a pentagon in two, along a straight line, in such a way that one of the resulting pieces is geometrically similar to the original pentagon? Since the newly created (smaller) pentagon has only one edge formed by the cut, its other four edges must obviously be segments of the original pentagon.

There are two general approaches that we can take. The first and most obvious approach is to construct the original pentagon with consecutive edge lengths in geometric progression, from the smallest up to the second-largest. Let A,B,C,D,E denote the five vertices of the original pentagon, and suppose that for some k less than 1 the edge lengths are AB = 1, BC = 1/k, CD = 1/k², and DE no greater than 1/k³. Also, let the interior angles at the vertices A, B,... be 120, 120, 120, 120, and something near 60 degrees. Rotating this figure 60 degrees and shrinking it by a factor of k makes four of the sides sit on top of the original sides, so this shows how the original pentagon can be cut to give a self-similar pentagon. Incidentally, if the reduction factor is 0.7548776... the figure we get is The Golden Pentagon, and the "other" piece that is cut off from the original pentagon is an equilateral triangle. This enables us to tile the plane with a geometric spiral of unequal triangles.

The second approach is to consider whether there might be solutions other than these simple "spiral" solutions, such that the edge lengths around the pentagon are arranged in an alternating sequence, and such that the reduced pentagon must be rotated by two vertices (instead of 1) to bring four of its edges into alignment with the edges of the original pentagon. This is indeed possible, and leads to a nice infinite family of solutions for any fixed scale factor k.

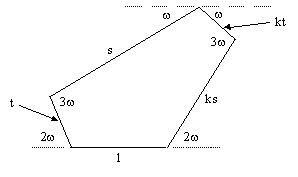
It's not hard to see that this can only work if the interior angles of the pentagon have one of two values, either α or β, and they must be arranged in the sequence α, β, α, β, β. In addition, two of the edges must be a factor of k times the respective edge in the unrotated orientation. Thus, we require a configuration as shown below

Notice that the two sizes of interior angles are

and the sum of the five interior angles, 2α + 3β, equals 3π as required. In order to make the edges meet, we must satisfy the following two simultaneous conditions relating the edge lengths s and t to the angle ω:

Solving these for s and t gives

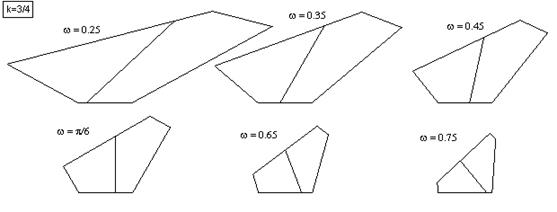
So, for example, with k = 3/4 we have an infinite family of pentagons that can be cut into two parts along a straight line, with one part being similar to the original pentagon. This is illustrated below for various values of ω.

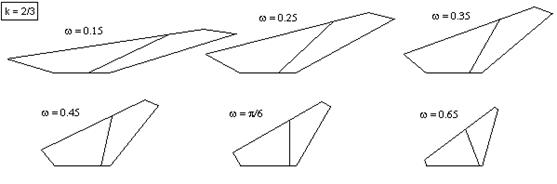
Likewise we can generate an infinite family for other values of k, such that the family with k = 2/3 illustrated below:

Notice that the "cut line" is always perpendicular to the base when the angle ω equals π/6.

Return to MathPages Main Menu