|
Sandford's Elevator |
|
|
|
People possess four things |
|
that are no good at sea: |
|
anchor, rudder, oars, |
|
and the fear of going down. |
|
Antonio Machado (tr. Robert Bly) |
|
|
|
An elevator car has a constant upward acceleration of a = 3 ft/sec2. If a bolt slips free from the bottom of the car and falls in 2 seconds to the bottom of the shaft, how high is the car when the bolt lands? (Neglect air resistance and assume the acceleration of gravity is g = 32 ft/sec2.) |
|
|
|
First Solution: Integrating the car's constant upward acceleration, from an arbitrary reference time t0 = 0, when the car's velocity is zero and its height is h0, to the time t1 when the bolt slips free, we have the car's velocity and height at the time t1: |
|
|
|
|
|
|
|
This is also the velocity and height of the bolt when it begins its free-fall. Integrating the constant downward acceleration of gravity, g, over the free-fall time T, and taking v1 and h1 as the initial conditions, we have |
|
|
|
|
|
|
|
Solving this equation for t1, and adding the time to fall, T, gives tf, the time when the bolt hits the bottom of the shaft: |
|
|
|
|
|
|
|
The elevator car has been accelerating upward at a since the initial instant t0 = 0, so its height at the time tf is |
|
|
|
|
|
|
|
Substituting the given values a = 3 ft/sec2, g = -32 ft/sec2, and T = 2 sec, we arrive at the result hf = 70 ft. |
|
|
|
Second Solution: At the time t the bolt and the car have the same height and velocity. Subsequently they recede from each other with a constant relative acceleration of a - g (i.e., 35 ft/sec2) for 2 seconds, at which point the bolt reaches the bottom of the shaft. Therefore, the height of the car when the bolt lands is just the relative separation between the bolt and the car after 2 seconds of a constant relative acceleration of 35 ft/sec2, which immediately gives the result hf = (1/2)(a-g)T2 = 70 ft. |
|
|
|
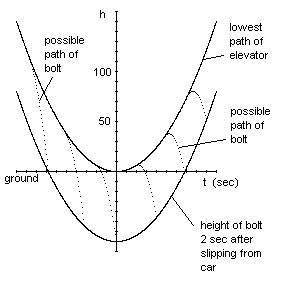
Supplemental Question: Since the statement of the problem gives us no other information, we assume the car experiences a constant upward acceleration of 3 ft/sec2 indefinitely. Based on this assumption, and assuming the car does not crash, what is the maximum height the car could have had when the bolt slipped free? The answer is 116.9878 ft, as illustrated by the left-most dotted path in the figure below: |
|
|
|
|
|
|
|
This occurs in the case when the elevator's path just skims the ground at the lowest point on its path. Of course, the elevator could have a higher trajectory, and it might seem that the bolt could be released from a higher point based on one of those higher trajectories. However, in order to reach the ground exactly 2 seconds following its release, the bolt would need to be released nearer and nearer to the elevator's lowest position, so the initial downward velocity of the bolt would be less, causing it to travel a lesser distance in the 2 second fall to the ground. The net result is that it would need to fall from a lesser height. |
|
|
|
On the other hand, if we remove the restriction that the elevator not crash, we can consider lower trajectories for the elevator than the one shown above. This would move the bolt's release time further to the left (for the left-most "possible path"), and allow the bolt to be released from a greater height. Given these allowances, there is no upper limit (classically) to how far above the ground the bolt might be released from an upwardly accelerating elevator, and still hit the ground in 2 seconds. |
|
|
|
Discussion: Sandford's Elevator problem is interesting because it illustrates how a problem's statement can influence our approach to it's solution. Suppose the problem had been stated as follows: |
|
|
|
An elevator has a constant upward acceleration of 3 ft/sec2. If a bolt slips free from the bottom of the elevator and falls under the influence of gravity, how far is the elevator from the bolt 2 seconds after they separate? |
|
|
|
In this form, we're compelled to take the relative rather than the absolute approach, and we arrive at the "Second Solution" immediately. However, by simply rephrasing the problem to say that the bolt hits the ground in two seconds, and asking how high above the ground the elevator is when the bolt lands, the reader is encouraged to treat the problem in the absolute sense, i.e., relative to the ground, even though the ground contact is not relevant to the problem. Thus, the reader is misled by a superfluous reference to the ground (i.e., the bolt striking the ground). The artfulness of the problem is in the fact that the reference doesn't seem superfluous, because the syllogistic loop is closed by asking, not how far the car is from the bolt, but how far the car is from the ground, even though they amount to the same thing. This creates the conceptual illusion that the ground is a significant element of the problem. Only when the arbitrary reference height h algebraically drops out of the "First Solution" do we realize that it was irrelevant to begin with. |
|
|
|
Of course, our a priori knowledge that the elevator shaft must have a bottom does impose certain conditions on the problem that can only be resolved via the absolute approach (i.e., the "First Solution"), which probably contributes to our psychological willingness to treat the ground as a significant element. The allusion to a "crash" in the supplemental problem makes explicit the underlying anxiety that inclines us to prefer the fixed ground to an indeterminately moving elevator car as our frame of reference. |
|
|